Attention Is All You Need paper review (3)
작성일
부족하겠지만 처음으로 내 스스로 논문을 읽고 정리해보려 함
영어실력의 부족으로 번역에 문제가 좀 있을 수 있으니 오역의 부분이 있다면 댓글을 달아주시면 좋을듯 함
- 1편 Attention Is All You Need Review (1)
- 2편 Attention Is All You Need Review (2)
- 3편 Attention Is All You Need Review (3)
- 4편 Attention Is All You Need Review (4)
Attention Is All You Need paper review (3)
3.3 Position-wise Feed-Forward Networks

attention sub-layer 에 더하여, encoder 와 decoder 안 layer 들 각각은 fully connected feed-forward network 를 포함함
fully connected feed-forward network 는 따로따로 그리고 똑같이 각각의 위치에 적용됨
fully connected feed-forward network 는 두개의 선형변환 사이에 ReLU 를 포함해서 구성됨
공식은 아래와 같음
\[FFN(x) = max(0, xW_1 + b_1)W_2 + b_2\]선형변환은 다른 위치에 대해 동일하게 적용되는 반면에 층간(layer to layer)에는 서로 다른 파라미터($W_1, W_2$)를 사용함
이것을 설명하는 다른 방법은 커널사이즈가 1인 두개의 convolution 과 같음
input 과 output 의 차원은 $d_{model} = 512$ 이고 fully connected feed-forward network 내부 hidden layer 는 $d_{ff} = 2048$ 의 차원을 가짐
3.4 Embeddings and Softmax

다른 시퀀스 변환 모델들과 유사하게 우리는 input 과 output 토큰들을 $d_{model}$ 차원의 벡터로 변환하기 위해 학습가능한 임베딩을 사용함
우리는 또한 decoder output 을 예측된 다음 토큰의 확률로 변환하기 위해 학습가능한 선형변환과 softmax 함수를 사용함
우리의 모델에서 우리는 두개의 임베딩 layer 와 softmax 이전의 선형 변환에 동일한 가중치행렬을 공유함
임베딩 layer 에서 우리는 공유되는 가중치들에 $\sqrt{d_{model}}$ 을 곱해줌
3.5 Positional Encoding


우리의 모델은 recurrence 와 convolution 을 포함하지 않기 때문에 다른 모델에서의 시퀀스의 순서를 사용하려면 우리는 시퀀스에서 토큰들의 상대적 또는 절대적 위치에대한 정보들을 주입해야만 함
이를 위해 우리는 encoder 와 decoder stack 의 가장 밑에 있는 input 임베딩에 “positional encodings” 를 더했음
positional encodings 는 임베딩과 더해질수 있도록 하기위해 같은 $d_{model}$ 차원을 가짐
학습가능한 또는 고정된 positional encoding 의 선택지는 매우 다양함
이 연구에서 우리는 다른 주기의 sine 과 cosine 함수를 사용함
\(PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}})\) \(PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}})\)
($pos$ 는 토큰의 위치, $i$ 는 벡터의 차원 인덱스)
즉, positional encoding 의 각각의 차원은 정현파(일정한 주기를 가지고 반복되는 주기함수)에 해당함
그 파장은 2$\pi$ 부터 10000 $\cdot$ 2$\pi$ 까지의 기하학적 진행을 형성함
우리는 고정 offset $k$ 에 대해 $PE_{pos+k}$ 가 $PE_{pos}$ 의 선형 함수로서 표현될 수 있기 때문에 이 함수는 모델울 상대적인 위치들에 따라 참조하는 방법을 쉽게 배울 수 있을거라고 가설을 세웠기 때문에 이러한 함수를 선택했음
우리는 또한 sine 과 cosine 대신에 학습가능한 posittional embeddings 를 사용한 실험을 했음
그리고 두개의 version 이 거의 동일한 결과를 내는 것을 알아냄 (Table 3 (E)번째 행을 봐바)
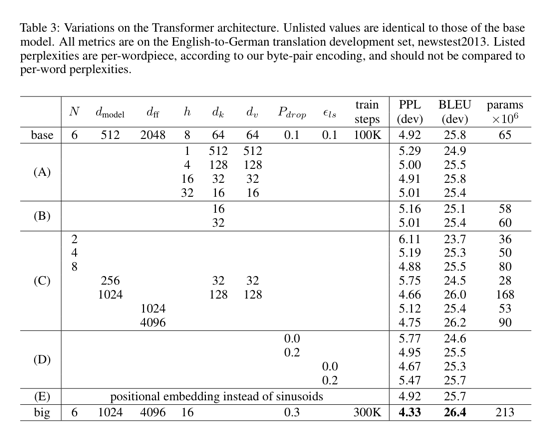
우리는 정현파 버전의 positional encodings 가 모델이 훈련 중에 만났던 것보다 더 긴 길이의 시퀀스 대해서도 추정할 수 있도록 허락하기 때문에 정현파 버전을 선택함
4 Why Self-Attention


이 섹션에서 우리는 다양한 self-attention 층의 측면을 $(x_1, …, x_n)$ 으로 표현된 다양한길이의 시퀀스를 전형적인 시퀀스 변환 encoder 또는 decoder 에서 hidden layer 와 같은 $(z_1, …, z_n)$ 같은 길이의 다른 시퀀스로 맵핑하기 위해 일반적으로 사용되는 recurrent 와 convolutional 층과 비교함
self-attention 의 사용을 동기부여하기 위해 우리는 세가지를 고려함
첫번째는 layer 당 총 계산 복잡도
두번째는 필요한 최소 순차적인 작업 수로 측정되는 병렬화될 수 있는 계산량
세번째는 network 에서 긴 범위의 dependencies 사이의 경로의 길이
긴 범위의 dependencies 를 학습하는 것은 많은 시퀀스 변환 task 에서 핵심 과제임
이런 dependencies 를 학습하는데 영향을 미치는 하나의 핵심 요인은 network 에서 forward 그리고 backward 신호를 가로지르기 위한 경로의 길이임
input 과 output 시퀀스에서 어떤 위치의 결합 사이의 이러한 경로가 짧을수록 긴 범위 dependencies 를 학습하는 것이 쉬워짐
그러므로 우리는 다른 layer 타입으로 구성된 network 에서 어떤 intput 과 output 위치 사이의 경로 길이의 최대값을 비교함
Table 1 에서 나타났듯이

self-attention 층은 모든 위치를 일정한 수의 순차적으로 실행되는 연산으로 연결함
반면에, recurrent 층은 순차적인 연산에 $O(n)$ 이 필요함
계산 복잡도면에서 self-attention 층은 word-piece 와 byte-pair representations 같은 기계번역에서 SOTA 모델에서 사용되는 문장 representations 에서 대부분 나타나는 시퀀스 길이 $n$ 이 $d$ 차원 보다 작을 경우 recurrent 층보다 빠름
매우 긴 문장을 포함하는 task 에 대해 계산적인 성능을 향상시키기 위해 self-attention 은 각각의 output 위치를 중심으로 input 시퀀스에서 $r$ 크기의 주변만 고려하도록 제한될 수 있음
이것은 최대 경로 길이를 $O(n/r)$ 로 증가시킴
우리는 나중에 이러한 접근방법을조사하기로 계획함
커널의 크기 $k$ 가 $n$ 보다 작은 하나의 convolutional 층은 모든 input 과 output 위치의 쌍을 연결하지 못함
network 에서 어떤 두개의 위치 사이의 가장 긴 경로의 길이를 증가시키려면 인접한 커널의 경우 $O(n/k)$ convolutional 층의 stack 이 필요함 또는 확장된 convolutions 의 경우 $O(log_k(n))$ 이 필요함
Convolutional 층은 $k$ 에 의해 일반적으로 좀더 recurrent 층 보다 비용이 듦
그러나 분리할 수 있는 convolutions 은 상당히 복잡도가 $O(k \cdot n \cdot d + n \cdot d^2)$ 으로 감소함
그러나 $k = n$ 일 때 조차 분리할 수 있는 convolution 의 복잡도는 우리의 모델에서 우리가 적용한 접근방식인 self-attention 층과 point-wise feed-forward 층의 결합과 같음
부과효과로서 self-attention 은 좀 더 해석가능한 모델을 산출할 수 있음
우리는 우리의 모델로부터 attention 분포를 조사함 그리고 appendix 에서 예를 보여주고 논의함
개별적인 attention head 들은 명확히 다른 task 를 수행하기 위해 학습할 뿐만 아니라 attention head 들이 문장의 구문론적 그리고 의미론적 구조와 관련된 행동을 나타내는 것을 보여줌

댓글남기기