늘 공부하는 딥린이

NLP Researcher

Attention Is All You Need paper review (2)

작성일

5 분 소요

부족하겠지만 처음으로 내 스스로 논문을 읽고 정리해보려 함

영어실력의 부족으로 번역에 문제가 좀 있을 수 있으니 오역의 부분이 있다면 댓글을 달아주시면 좋을듯 함

Attention Is All You Need paper review (2)

2. Background

순차 계산을 줄이려는 목표는 Extended Neural GPU, ByteNet 그리고 ConvS2S 의 기반을 형성했음

이것들 모두 기본 block 으로 모든 input 과 output 의 위치에 대해 병렬적으로 hidden representation 을 계산하는 CNN 을 사용함

이 모델들에서는 임의의 input 과 output 이 둘로부터의 신호를 연관짓는데에 필요한 계산의 수가 그 위치 사이의 거리에 따라 증가함

ConvS2S 에 대해서는 선형적으로 그리고 ByteNet 에 대해서는 대수적으로 증가함

이것은 먼 위치들 사이의 dependency 를 학습하는데 더 어럽게 만듦

Transformer 에서는 가중평균된 위치 때문에 효과적인 해결방법이 감소함에도 불구하고 Multi-Head Attention 이 상쇄하는 효과로 상수번의 계산량으로 줄임

때때로 intra-attention 이라고 불리는 Self-attention 은 sequence(연속된 글? 흐름?)의 representation(표현)을 계산하기 위해 하나의 토큰이 다른 위치의 토큰들과 연관짓는 attention 기법임

Self-attention 은 reading comprehension(독해), abstractive summarization(요약), textual entailment(두 문장이 주어졌을 때, 첫 번째 문장이 두 번째 문장을 수반하는가 혹은 위배되는가?) 그리고 learning task-independent sentence 을 포함한 다양한 task 에서 성공적으로 사용되고 있음

End-to-end 메모리 네트워크는 정렬된 시퀀스의 RNN 대신 recurrent attention 기법에 기초함

그리고 단일 언어 질의응답 task 와 언어 모델링 task 에서 좋은 성능을 보여주고 있음

그러나 우리가 아는한 Transformer 는 정렬된 시퀀스 RNN 또는 Convolution 없이 input 과 output 의 representation 을 계산하기 위해 오로지 self-attention 에 의존한 첫번째 변환모델임

다음 섹션에서 우리는 self-attention 유도하고 다른 모델들을 넘어선 장점에 대해 토론하면서 Transforemr를 소개할 것임

3. Model Architecture

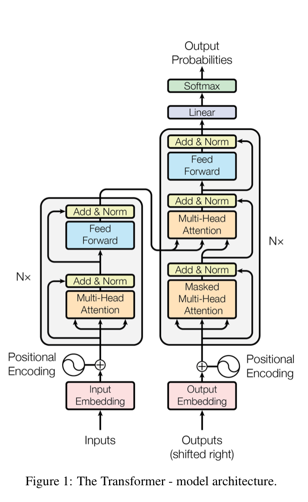
대부분의 경쟁력있는 신경망 시퀀스 변환 모델은 encoder-decoder 구조를 가짐

여기에 encoder 는 토큰으로 표현되는 input sequence 인 ($x_1$, …, $x_n$)를 연속적인 표현의 sequence 인 $z = (z_1, …, z_n)$ 으로 매핑함

$z$ 가 주어지면 decoder 는 그때 한 시점에서 하나의 element(토큰)의 output sequence 인 ($y_1, …, y_m$) 생성함

각 단계에서 모델은 다음 값을 생성할 때 추가적인 input 으로서 이전에 생성된 값(symbols)을 사용하기 때문에 auto-regressive 함

Transformer 는 쌓여진 self-attention 과 point-wise fully connected layers 를 Figure 1 에서 각각 왼쪽과 오른쪽에서 보여지는 encoder 와 decoder 에서 둘다 사용하는 전반적인 구조를 따름

3.1 Encoder and Decoder Stacks

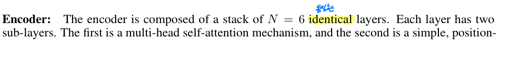
인코더는 6개의 동일한 layer 를 쌓아서 구성됨

각각의 layer 는 두개의 sub-layer 를 가짐

첫번째는 multi-head self-attention mechanism 이고 두번째는 단순한 point-wise fully connected feed-forward network 임

우리는 두개의 sub-layer 각각에 residual connection 을 적용하고 후에 layer normalization 을 적용함

즉, 각각의 sub-layer 의 output 은 $LayerNorm(x + Sublayer(x))$ 이 되고, 이 때 $Sublayer(x)$ 는 sub-layer에 의해서 구현된 함수임

residual connection 을 가능하게 하기 위해 모델에서 embedding layer 뿐만 아니라 모든 sub-layer 는 512 차원의 output 만을 생성함

디코더도 6개의 동일한 layer 를 쌓아서 구성됨

각각의 인코더에서 2개의 sub-layer 에 더해 디코더는 쌓여진 encoder 의 output 에대해 multi-haed attention 을 수행하는 세번째 sub-layer 를 삽입함

인코더와 유사하게 각 sub-layer 마다 residual connection 을 적용하고 후에 layer normalization 을 적용함

또한 우리는 쌓여진 decoder 에서 현재 위치가 후속 위치를 참조하는 것을 막기 위해 self-attention sub-layer 를 수정함

output embedding 들이 하나의 위치에 의한 차이라는 사실과 결합해서 이 masking 은 $i$ 번째 위치의 예측은 $i$ 보다 이전 위치의 알려진 output 에만 의존할 수 있게끔 보장함

3.2 Attention

attention 함수는 query, keys, values 그리고 output이 모두 벡터일 때, query 와 key-value pair 세트를 output 으로 맵핑하는 것으로 설명될 수 있음

output 은 각각의 value 에 할당된 weight 는 query 와 대응하는 key 의 호환성 함수에 의해 계산되었을 때, values 의 가중합으로서 계산되어짐

3.2.1 Scaled Dot-Product Attention

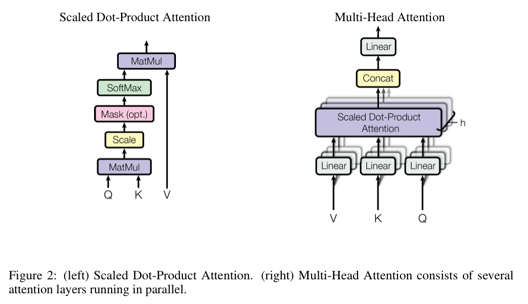
우리는 우리의 특별한 attention 을 “Scaled Dot-Product Attention” 이라고 부름

input 은 $d_k$ 의 차원을 가지는 queries 와 keys 그리고 $d_v$ 의 차원을 가지는 values 로 구성됨

우리는 query 하나와 모든 keys 내적을 계산하고 각각을 $\sqrt{d_k}$ 로 나눠주고 values 들에 대한 weights 를 얻기위해 softmax 를 적용함

실제로는 query 전부를 하나의 행렬 Q 로 묶어서 동시에 attention 함수가 계산됨

key 와 value 들은 행렬 K 와 V 로 묶여짐

우리는 아래과 같이 output 행렬을 계산함

\[Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]

가장 일반적으로 사용되는 attention 함수 2개는 additive attention 과 dot-product(곱셈) attention 임

Dot-product attention 은 $\frac{1}{\sqrt{d_k}}$ 을 곱해주는 요소를 제외하고는 우리의 알고리즘과 동일함

Additive attention 은 하나의 은닉층으로 feed-forward network 를 사용한 호환성 함수를 계산함

이 둘은 이론상 동일한 복잡도를 갖는 반면, dot-product attention 은 실무에서 매우 최적화된 행렬곱 code 로 구현될 수 있기 때문에 좀 더 빠르고 좀 더 space-efficient 함

$d_k$ 의 값이 작은 경우 두가지 mechanism 은 유사한 성능을 내는 반면, $d_k$ 의 값이 큰 경우 스케일링 없이 additive attention 는 dot-product attention 을 능가함

우리는 $d_k$ 가 큰 경우 dot product 도 크기가 커져서 softmax 함수를 극도로 작은 gradient 들을 가진 부분으로 밀어낸다고 의심함

이런 효과를 상쇄하기 위해 우리는 $\frac{1}{\sqrt{d_k}}$ 로 dot product 를 스케일링 함

3.2.2 Multi-Head Attention

$d_{model}$ 차원의 keys, values 그리고 queries 를 가지고 하나의 attention 함수를 수행하는 대신에, 우리는 각각 queries, keys 그리고 values 를 $d_k$, $d_k$ 그리고 $d_v$ 차원으로 선형 사영하는 $h$ 개의 다른 학습가능한 선형 사영(linearly project)을 하는것이 유익함을 발견함

queries, keys 그리고 values 의 사영버전들 각각에서 우리는 $d_v$ 차원의 output 값들을 산출하면서 병렬적으로 attention 함수를 수행함

결과로 나온 output 들은 Figure 2 에서 묘사된 것처럼 합쳐지고 다시 최종 결과물로서 선형 사영됨

Multi-head attention 은 다른 위치에서 다른 표현 부분공간(subspace)으로부터 정보에 결합적으로 참조할 수 있도록 모델에게 허락함

단일 attention head 에서는 평균이 정보에 결합적으로 참조하는 것을 억제함

이 연구에서 우리는 $h = 8$ 의 병렬적인 attention layer 들과 head 들을 사용

이들 각각에 대해 우리는 $d_k = d_v = d_{model}/h = 64$ 를 사용함

각각의 head 의 차원이 줄었기때문에 전체 계산 비용은 전체 차원에대한 단일 attention 계산비용과 유사함

3.2.3 Applications of Attention in our Model

Transformer 는 3가지 다른 방법으로 multi-head attention 을 사용함

  1. encoder-decoder attention 에서, query 들은 이전 decoder layer 로부터 오고 저장된 key 와 value 들은 encoder 의 결과로부터 옴
    • 이것은 디코더의 모든 위치들이 input sequence 의 모든 위치를 참조할 수 있도록 허락함
    • seq2seq 모델에서의 전형적인 encoder-decoder attention mechanism 을 모방함
  2. encoder 는 self-attention layer 를 포함함
    • self-attention layer 에서 key, value, query 들은 모두 같은 장소로부터 옴
    • 이 경우엔, 인코더의 이전 layer 의 output 임
    • encoder 에서 각각의 위치는 encoder 의 이전 layer 에서 모든 위치를 참조할 수 있음
  3. 유사하게, decoder 의 self-attention layer 들은 decoder 의 각각의 위치에서 해당 위치를 포함해 이전까지의 decoder 의 모든 포지션을 참조하는 것을 허락함
    • 우리는 auto-regressive 특성을 보존하기위해 decoder 에서 leftward 의 정보흐름(미래 시점의 단어들을 미래 조회함에 따라 현재단어 결정에 미칠 수 있는 영향)을 막아야 함
    • 우리는 이런 불법적인 연결에 해당하는 softmax 의 input 에서 모든 값에 마스킹(-inf 를 줌) 함으로써 scaled dot-product attention 안에 이것을 구현함
    • Figure 2 를 봐

이 다음 부분은 다음편에서 작성하도록 하겠음

댓글남기기

참고