Day_30 02. Transformer (2)

Transformer (cont’d)

Transformer: Multi-Head Attention

• 지난 post 에서 배운 self-attention 모듈을 좀 더 유연하게 확장한 Multi-Head Attention 에대해 알아보자.

• The input word vectors are the queries, keys and values
• In other words, the word vectors themselves select each other
• Problem of single attention
  • Only one way for words to interact with one another
• Solution
  • Multi-head attention maps $Q, K, V$ into the $h$ number of lower-dimensional spaces via $W$ matrices

• Then apply attention, then concatenate outputs and pipe through linear layer

  

  

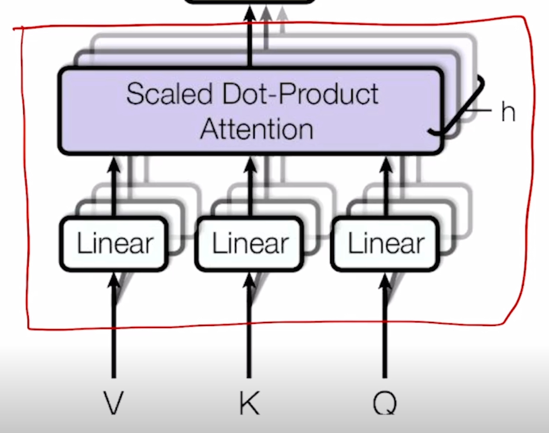
• 위 그림에서 앞서 배운 attention 모듈을 이러한 네모 블럭으로 나타내보면

• Attention 모듈에 Query, Key, Value vector 를 입력으로 주게되고

  

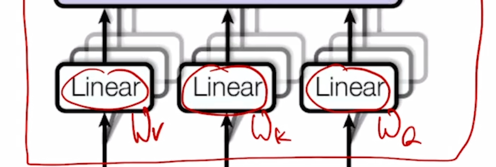
• 그 다음엔 각 vector 들을 각각의 선형변환을 해주는 $W^Q$, $W^K$, $W^V$ 을 통과해서 선형변환을 한 후 각각의 Query vector 에 대해서 이 Key 와 Value vector 의 대한 attention 및 Value vector 의 가중합을 통해서 각 Qeury vector 의 대한 encoding 된 vector output 을 얻게 됨

  

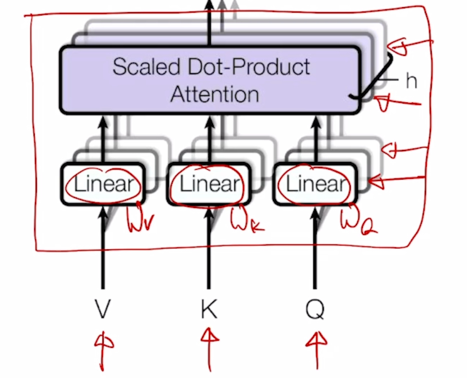
• 아래쪽에 중첩된 block 들이 보일텐데 이것은 바로 동일한 Query, Key, Value vector 들에 대해서 동시에 병렬적으로 여러버전의 attention 을 수행한다는 뜻이 됨

  

• 구체적으론 $W^Q$, $W^K$, $W^V$ 가 하나의 행렬 set 만 존재하는게 아니라 여기에서 보이듯 여러버전의 행렬들이 존재하고 i 번째의 attention 에서는 그 해당하는 i번째의 $W_i^Q$, $W_i^K$, $W_i^V$ 를 써서 선형변환을 한 후 attention 을 수행해서 Query vector 에 대한 encoding vector 들을 얻게 됨

  

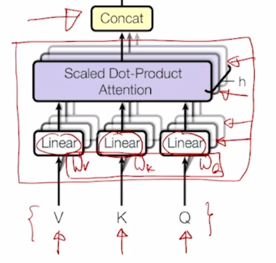
• 그러면 여기서 서로 다른 버전의 attention 의 개수만큼 동일한 Query vector 에 대한 서로 다른 버전의 encoding vector 가 나오고 그 encoding vector 를 모두 concat 함으로써 해당 Query vector 에 대한 encoding vector 를 최종적으로 얻게 됨

• 그리고 여러 버전의 attention 을 수행하기 위한 선형변환 matrix 이것들을 서로 다른 head 라고 부름

• 다수의 버전의 attention 을 수행한다는 뜻으로 Multi-Head attention 이라고 부름

• 그러면 Multi-Head attention 이 필요한 이유에 간략히 설명해보자.
• 동일한 sequence 가 주어졌을 때에도 어떤 특정한 Query word 에 대해서 서로 다른 기준으로 여러 측면에서의 정보를 뽑아와야 될 필요가 있을 수 있음
• 가령 여러문장으로 이루어져있긴 하지만 어떤 하나의 sequence 로서 볼 수 있는 “I went to the school” 그 다음엔 “I studied hard” 그 다음엔 “I came back home” 그 다음엔 “I took the rest” 이러한 주어진 여러 문장이 있을 때에 첫번째로 주어진 “I” 라는 Query word 에 대한 encoding 을 수행을 하기 위해서는 먼저 그 “I” 라는 주체가 한 행동을 중심으로 즉, “went”, “study” 그 다음엔 “came back home” 그 다음엔 “took the rest” 이러한 주체가 하는 행동을 중심으로 하는 정보를 뽑아올 수 있게 되고 또 다른 측면에서는 “I” 라는 주체가 존재하던 장소의 변화 가령 “to the school” 해서 학교에 있엇고 그 다음엔 집으로 돌아왔다라는 장소의 해당하는 정보를 또 뽑을 수 있게 됨
• 이런 방식으로 서로 다른 측면의 정보를 병렬적으로 뽑고 그 정보들을 다 합치는 형태로 attention 모듈을 구성할수가 있음

• 그래서 각각의 Head 가 이런 서로 다른 정보들을 상호 보완적으로 뽑는 역할을 하게 됨

• 이를 도식화해서 나타내면

• Example from illustrated transformer

  

  

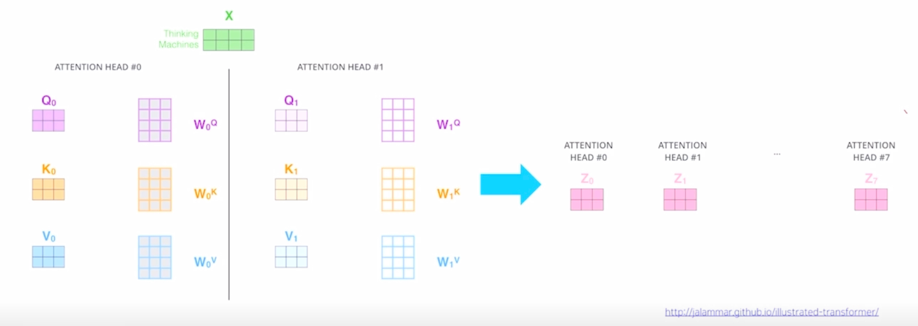
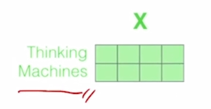
• 이전 post 에서 봤던 두 단어로 이루어진 sequence 에 대해서 2개의 서로 다른 Head 가 존재한다라고 가정하면

  

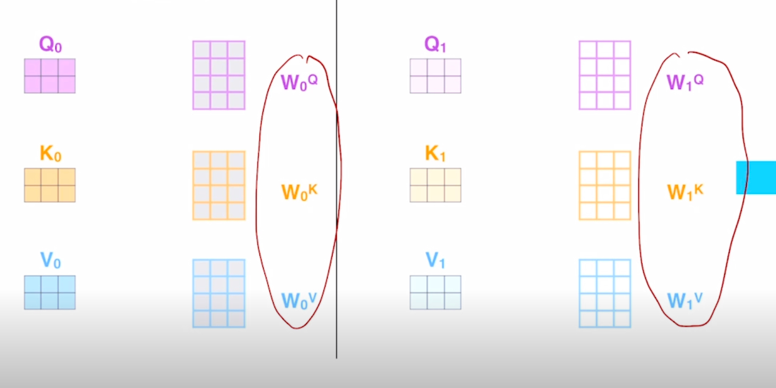
• 동일한 X matrix 에 대해서 각각의 head 별로 존재하는 선형 변환 matrix 를 통해서

  

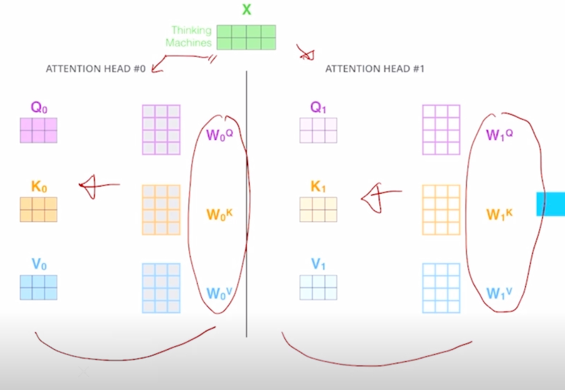
• 그 때 얻어지는 Query, Key, Value vector 들을 가지고 첫번째 head 내에서 그리고 두번째 head 내에서의 encoding vector 결과값을 얻게 됨

  

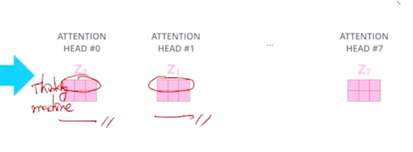
• 그러면 역시 “Thinking”, “Machines” 에 해당하는 encoding vector 가 되고 각각의 head 에서 얻어진 2개의 결과 vector 를 simplily concat 을 한 형태로 작성할 수 있음

  

  

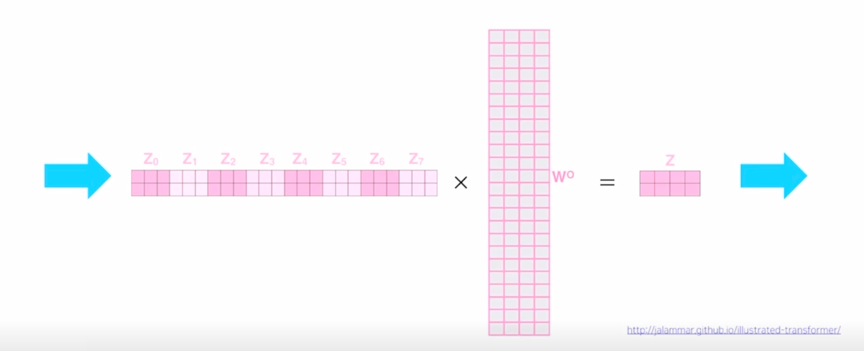
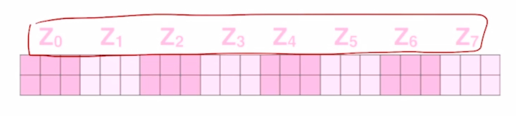
• 그러면 head 가 총 8개가 있다고 할 때,

  

• 각 head 별로 3차원 vector 의 output 을 얻었다면

  

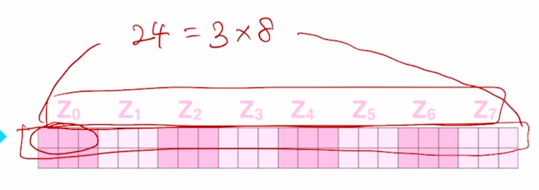
• 그것을 모두다 concat 을 하면 차원수가 총 24차원의 즉, 이는 각 head 에서 나온 Value vector 의 차원과 총 head 의 개수의 곱으로 이루어짐

• 그리고 당연히 이 row vector 는 Query word 들의 개수인 “Thinking”, “Machines” 에 해당하는 각각의 vector 가 됨

  

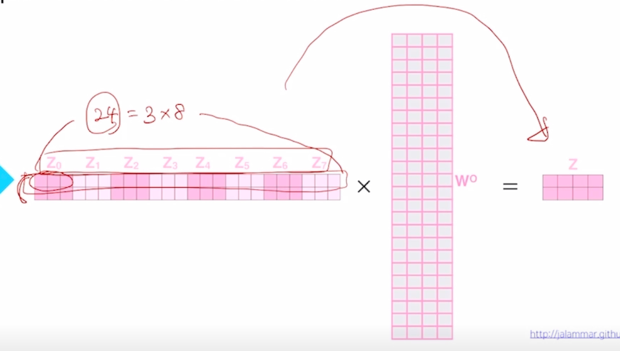
• 그 다음으로는 Linear 라는 operation 을 수행하게 되는데 여기서는 24 dimension 의 vector 를 특정한 원하는 dimension 으로 줄여주는 역할을 하는 또다른 선형변환을 수행하게 됨

• 여기서 4차원의 vector 를 최종적으로 얻게 하는 24 x 4 에 해당하는 선형변환 layer 를 하나 더 두고 최종 output 을 얻어내게 됨

• 그러면 Attention 모델의 계산량이나 memory 요구량의 측면에서 특성을 살펴보고 기존의 RNN 기반의 sequence encoding 과의 비교를 해보자.

• Maximum path lengths, per-layer complexity and minimum number of sequential operations for different layer types
  • $n$ is the sequence length
  • $d$ is the dimension of representation
  • $k$ is the kernel size of convolutions
  • $r$ is the size of the neighborhood in restricted self-attention

  

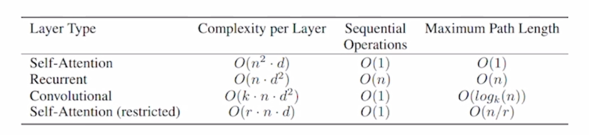
• Self-Attention 에서 주된 계산 부분을 차지하는 것은 $ softmax(\frac{QK^T}{\sqrt{d_k}}) V $ 의 형태의 연산에서 $QK^T$ 부분에 해당

  

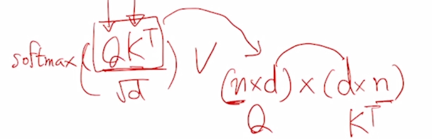
• $QK^T$ 같은 경우 sequence 길이가 $n$ 이라고 하고 각각의 Query 와 Key 에 대한 dimension 이 $d$ 라고 한다면 그러면 여기서는 $n$ 개의 Query 와 $n$ 개의 Key 에 대한 $d$ dimension 의 모든 가능한 pair 에 대한 내적값을 계산해야 함
• 즉 그래서 여기서는 ($n \times d$) 가 $Q$ 가 되고 이걸 ($d \times n$) 개 한게 $K^T$ 가 됨

• 그러면 특정한 Query 와 특정한 Key 에 대해서 $d$ dimension 의 내적을 계산해야 되고 $d$ dimension 의 내적은 기본적으로 $d$ 만큼의 곱셈 및 덧셈을 수반하게 됨

  

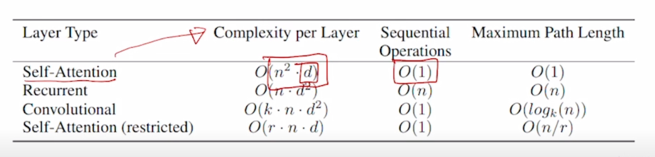
• 그것을 모든 Query 와 Key 의 조합에 대해서 수행해야 하기 때문에 $n^2 \cdot d$ 만큼의 계산이 가장 많은 부분의 계산을 차지함

• 그렇지만 이러한 행렬연산은 GPU 의 core 수가 충분히 많다면 sequence 가 아무리 길든 혹은 dimension 수가 아무리 크든 이 모든 계산을 GPU 가 가장 특화된 행렬연산의 병렬화를 통해서 core 수가 무한정 많다는 전제하에 이것을 모두다 한번에 계산할 수 있음

  

• 그에비해 RNN 의 경우는 주로 필요로하는 계산량이 self-attention 모델과는 달리 $n \cdot d^2$ 으로 표현됨

  

• 이것은 기본적으로 각 timestep 에서 계산되는 과정을 살펴볼 때

  

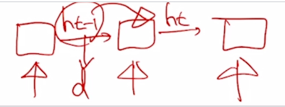
• 왼쪽에서 넘어오는 $h_{t-1}$ 의 vector 가 다음 timestep 의 $h_t$ 에 어떤 변환이 되어서 참여할 때에 $h_{t-1}$ 의 dimension 이 $d$ 라고 하면 vanila RNN 의 구조에서 봤던 것처럼

  

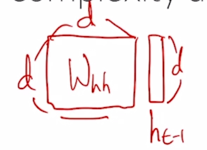
• $d$ dimension 의 vector $h_{t-1}$ 이고 그리고 우리가 곱하는 $W_{hh}$ 이는 역시 $d$ dimension vector 를 입력으로 받아 $d$ dimension 의 vector 를 출력으로 내어주기 때문에 이러한 행렬과 곱해야 함

  

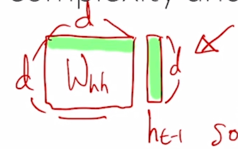
• 이 행렬과 벡터의 곱을 할 때는 각각의 $W_{hh}$ 의 row vector 와 $h_{t-1}$ 이 내적을 수행해야 하는데 이 경우 총 $d$ 번의 계산이 필요함

• 그 다음엔 각각의 $W_{hh}$ 의 row vector 와 이 계산을 수행해야 하기 때문에 결국 $d^2$ 만큼의 계산량이 필요하게 됨

  

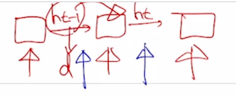
• 그러면 이 계산을 매 timestep 마다 순차적으로 수행해줘야 함

  

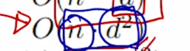
• 그래서 여기서 가장 핵심이 되는 계산량은 timestep 개수인 $n$ 에 각 timestep 에서 일어나는 hidden state vector 를 $W_{hh}$ 에 의해서 변환할 때 필요로 하는 계산량인 $d^2$ 만큼의 계산이 필요하게 됨

  

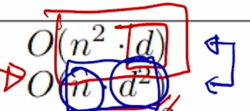
• 그러면 이 두 계산량의 차이의 측면에서 memory 요구량의 차이를 살펴보자.

• 먼저 이러한 정보들은 Forward Propagation 및 Back propagation 과정에서 모두 다 memory 에 저장하고 있어야 함
• 그래야 Forward Propagtion 했을때의 세부적인 값들을 다 저장해두고 그것들을 다시 Back propagation 해서 gradient 를 역전파하는 과정중에 이 정보를 사용해햐 함
• 그러면 $d$ 라는 값은 RNN 이나 self-attention layer 를 정의할 때 임의로 정할 수 있는 hidden state vector 의 dimension 으로서 하이퍼파라미터가 되고 이 값은 특정값으로 정할 수 있음
• 그렇지만 $n$ 이라는 것은 입력 데이터의 sequence 가 길면 길수록 임의로 길이를 고정된 값으로 사용할 수 있는 것이 아니라 주어진 입력에 따른 가변적인 값을 가지는 형태가 됨
• 그러면 좀 더 긴 sequence 를 처리하게 되면 그러한 입력이 주어졌을때는 self-attention 모델에서는 sequence 길이의 제곱에 비례하는 계산량과 메모리 사이즈가 필요하게 됨
• 그렇지만 RNN 모델에서는 그에비해 sequence 길이에 단지 1차 함수로서 비례하는 형태가 되기 때문에 일반적으로 self-attention 에서는 RNN 보다 훨씬 더 많은 메모리 요구량이 필요하게 됨
  • 다시말하면 모든 Query 와 모든 Key vector 들 간의 내적값을 저장하고 있어야 하기 때문

• 여러 계산들 중에 병렬화가 가능한 측면에서의 RNN 과 self-attention 모델의 차이를 살펴보자.

  

• 앞에서 말했듯 self-attention 은 sequence 길이가 아무리 길더라도 GPU core 수가 충분히 뒷받침 된다면 모든 계산을 동시에 수행할 수 있음

• 그렇지만 RNN 의 경우는 앞서 말한것처럼 기본적인 RNN 의 특성은 $h_{t-1}$ 을 계산을 해야만 재귀적으로 그 다음 timestep 의 RNN 에 vector 를 입력으로 넣어줄 수가 있고 그래서 $h_t$ 를 계산하기 위해서는 $h_{t-1]$ 이 계산될 때까지 기다릴 수 밖에 없음

  

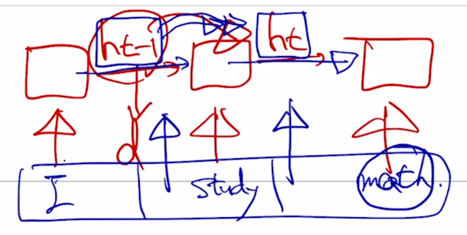
• 그래서 sequence data 에서 입력은 처음부터 모두 다 주어져있는 그래서 가능하다면 동시에 다 처리를 할 수 있는 그런 형태로 입력이 주어지지만 RNN 의 계산과정의 특성상 각 timestep 에서 계산되는 hidden state vector 는 절대 병렬화가 불가능하게 됨
• 따라서 RNN 의 Forward propagation 그리고 마찬가지로 Back propagation 에서는 sequence 길이의 비례한 병렬화가 불가능한 sequential 한 operation 이 필요하게 됨
• 이러한 사실 때문에 일반적으로 self-attention 기반의 transformer 모델은 학습은 훨씬 더 RNN 보다 빨리 진행될 수 있음

• 그렇지만 RNN 보다 더 일반적으로 많은 양의 memory 를 필요로 하게 됨

• 그 다음으로 살펴볼 요소는 Maximum Path Length 라는 것인데 이것은 지난 post 에서 논의했던 Long-Term dependency 와 직접적으로 관련됨

• 가령 여기서는 sequence gap 이 차이가 클 때

  

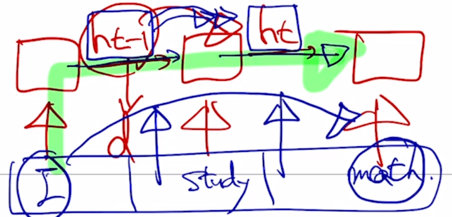
• 여기 “math” 라는 단어가 “I” 라는 정보를 잘 반영해서 encoding 을 수행하려면 RNN 의 경우는 RNN layer 를 timestep 의 차이만큼 지나가야함

  

• Path length 는 길이가 $n$ 인 sequence 에 대해서 가장 끝에 있는 단어가 가장 앞에 있는 정보를 참조하기 위해서는 어쩔 수 없이 $n$ 번의 RNN layer 를 통과해야 함

  

• 그렇지만 self-attention 에서는 가장 끝에 있는 단어라 하더라도 가장 처음에 나타나는 단어를 그냥 인접한 단어와 별다른 차이가 없는 동일한 Key 와 Value vector 로 보기 때문에 필요하다면 timestep 이 차이가 많이 나는 경우에도 필요한 만큼 정보를 attention 에 기반한 유사가 높도록 함으로써 정보를 직접적으로 한번에 가져올 수 있게 됨
• 따라서 self-attention 이 이러한 방식에 의해서 long-term dependency 를 근본적으로 해결한 결과가 나타남

Transformer: Block-Based Model

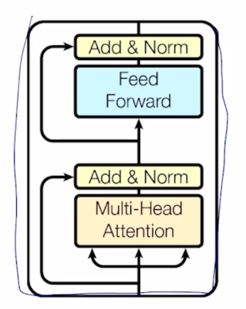
• 지금까지는 Multi-Head attention 을 배웠고 Transforemr 모델에서는 Multi-Head attention 을 핵심모듈로 해서 이와 덧붙여서 추가적인 여러 후처리를 거쳐서 하나의 모듈을 구성하게

• Each block has two sub-layers
  • Multi-head attention
  • Two-layer feed-forward NN (with ReLU)
• Each of these two steps also has
  • Residual connection and layer normalization:
  • $LayerNorm(x + sublayer(x))$

  

• 그러면 이 그림에서

  

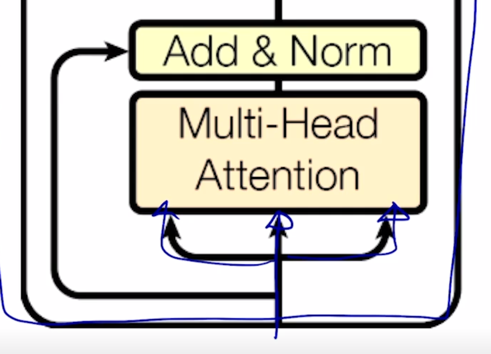
• 들어가는 이 3개의 화살표는 앞서 배웠던 Value, Key, Query 자격으로 들어가는 vector 들에 해당하고
• self-attention 같은 경우 즉, “I study math” 라는 문장을 자기자신 sequence 에 대해서 각 단어들의 대한 encoding 을 수행하려면 그 3개의 vector set 가 각각 Query, Key, Value 의 자격으로 들어가게 됨

• 그러면 내부적으로 $W^Q$, $W^K$, $W^V$ 이런 변환을 각 Head 별로 거치고 그 다음에 나온 encoding 된 vector 들을 각 Head 별로 concat 해서 output layer 로서 존재하던 추가적인 선형변환을 통해 각 word 별로의 encoding vector 가 최종적으로 나오게 됨

  

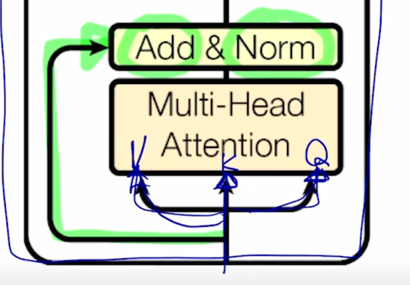
• 그렇지만 여기서 더 추가적인 연산은 residual connection 이라고 부르는 Add 라는 operation 을 수행한 후 추가적으로 layer normalization 이라는 것을 수행하게 됨

  

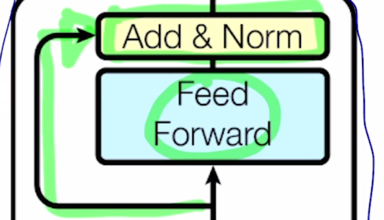
• 추가적으로 Feed Forward network 를 또 통과하고 그 다음엔 추가적으로 residual connection 및 layer normalization 을 수행하게 됨

• 그러면 Add 에 해당하는 residual connection 에 대해서 먼저 얘기해보자.

• 이 residual connection 은 computer vision 쪽에서 깊은 layer 의 Neural net 을 만들 때 gradient vanishing 문제를 해결하여 학습은 안정화 시키면서 layer 를 계속 쌓아감에 따라 더 높은 성능을 보일 수 있도록 하는 그런 효과적인 모델임

  

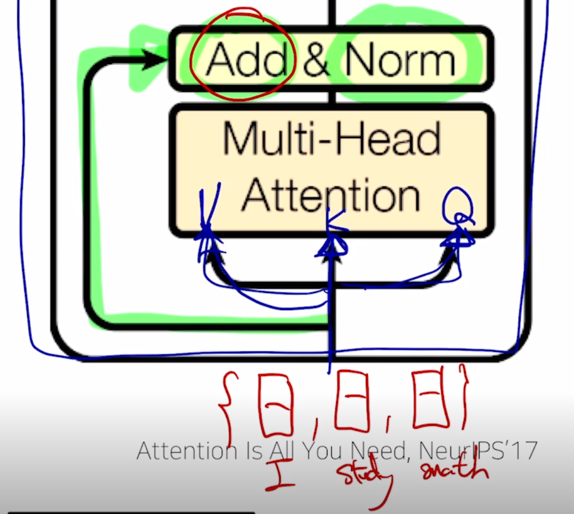
• “I study math” 에 해당하는 입력벡터가 2차원 벡터로 구성되어 있다고 하자.

  

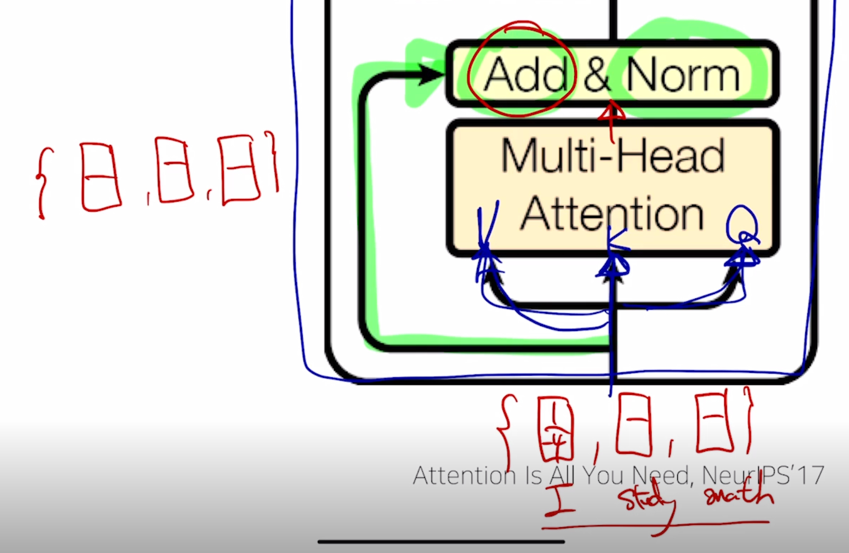
• 이 벡터가 “I” 의 경우 [1, -4] 라고 하고 Multi-Head attention 을 통과해서 나온 output vector 를 왼쪽에 써서 그 벡터들 역시 “I study math” 에 해당하는 각 단어별로의 encoding 벡터가 됨

  

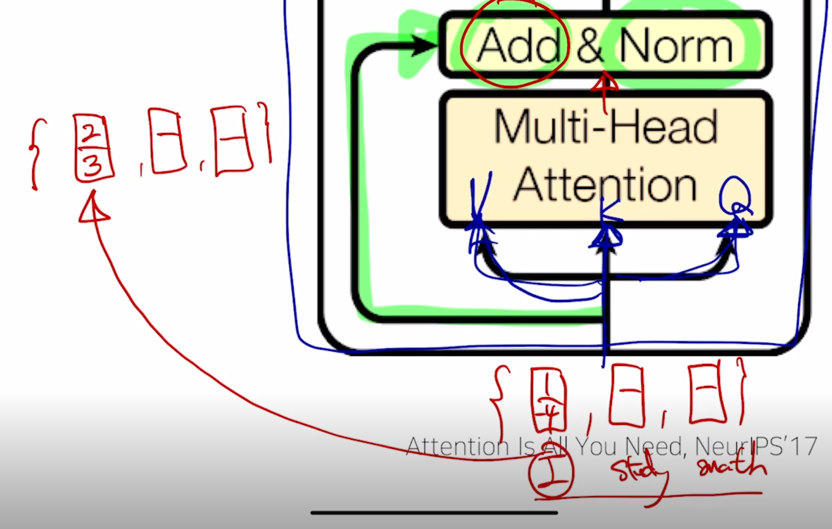
• 그러면 그 벡터가 가령 [2, 3] 이라고 하고 “I” 에 대한 encoding 벡터의 결과값이 나왔다고 하면

  

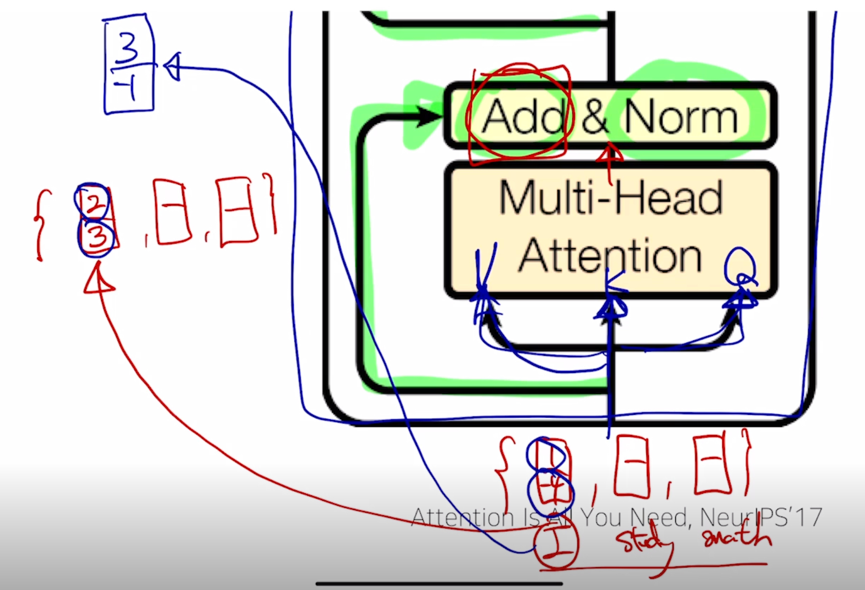
• 이 2개의 벡터를 residual connection 에 의해서 1 과 2를 더해서 3을 만들고 -4 와 3을 더해서 -1을 만들어서 최종적으로 “I” 에 대한 encoding 벡터를 얻어내게 됨

• 그래서 이러한 방식이 residual connection 에서 해주는 역할이 됨

  

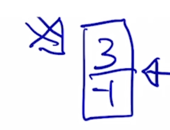
• 그러면 결국 만들고자 하는 벡터가 이 벡터라고 하면

• Multi-Head attention 모듈에서는 입력값 대비 만들고자하는 벡터에 대한 차이값만을 attention 모듈에서 만들어주어야 함
• 이런 과정을 통해 gradient vanishing 문제도 해결하고 학습도 좀 더 안정화 시킬 수 있게 됨
• 그리고 residual connection 을 적용하기 위해서는 입력 벡터 [1, -4] 와 encoding 의 output 으로 나타나는 출력벡터 [2, 3] 간의 dimension 이 정확하게 동일하도록 유지되어야 함

• 그래야 각 dimension 별로 해당 원소값을 더해서 최종 동일한 차원을 가진 벡터 [3, -1] 를 만들어 줄 수 있게 됨

• 이런 관점에서 앞서 얘기했던 output layer 에 해당하는 선형변환에서는 일시적으로 그 Head 수가 많아짐에 따라서 encoding vector 들의 output 들이 다 concat 이 되면서 차원이 늘어나게 되고 그 늘어난 차원을 원래 입력벡터와 더해주어야 하기 떄문에 입력벡터의 차원이었던 4차원과 동일한 차원을 가지 벡터로 변환을 해주는 그런 역할을 수행해야 함

• 다음은 Norm 이라고 쓰여진 layer normalization 연산에 대해서 살펴보자.

Transformer: Layer Normalization

• Layer normalization changes input to have zero mean and unit variance, per layer and per training point (and adds two more parameters)

  

  

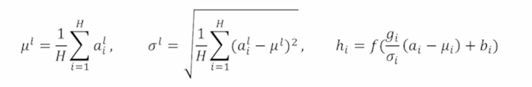
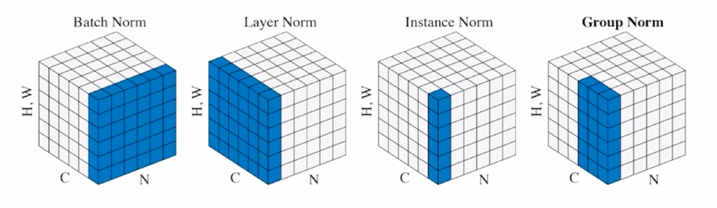
• 뉴럴넷 혹은 딥러닝에서 다양한 normalization 기법들이 존재함
• 가령 Batch Norm, Layer Norm, Instance Norm, 그리고 또 좀 더 최근에 발표된 Group Norm 이라는게 존재함

• 기본적으로 여러 normalization layer 는 주어진 다수의 sample 들에 대해서 그 값들의 평균을 0 그 분산을 1로 만들어 준 후 우리가 원하는 평균과 분산을 주입할 수 있도록 하는 그런 선형변환으로 이루어짐

  

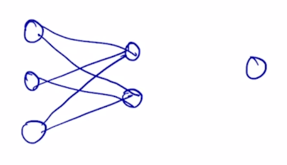
• 가령 Batch Norm 의 경우 어떤 뉴럴넷이 구성되어 있는 경우에

  

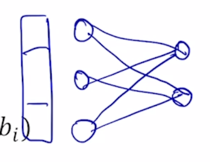
• 배치사이즈가 가령 3이라고 하면 입력 layer 에 3차원 벡터를 총 3개의 데이터 instance 에 대해서 넣어줄 것이고

  

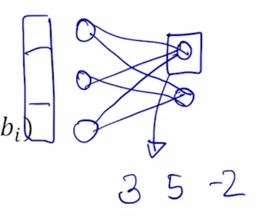
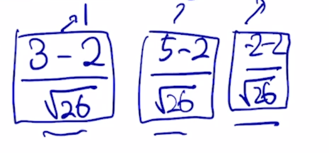
• 이 경우 나온 Forward propagation 당시 측정 node 에서 발생되는 값이 혹은 계산되는 값이 3개의 batch 내에 각 data instance 에 대해서 가령 3 5 -2 가 나왔다고 하자.

• 이 특정 layer 의 특정 node 에서 발견된 이 값들에 대해서 이 값들이 어떤 값들이었든지 간에 이 값들의 대한 평균을 0 그리고 분산을 1로 만들어주는 변환을 수행할 수 있게 됨

  

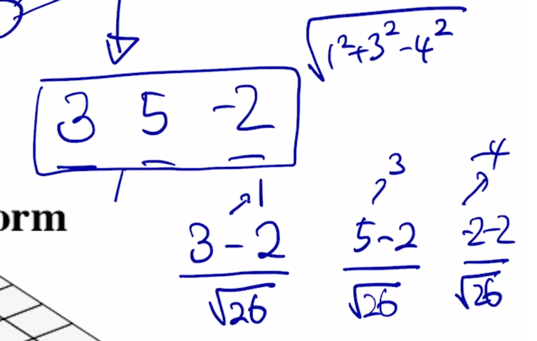
• 이는 3개의 값에서 평균값을 구하면 그 값이 2 가 되고 그래서 그 값을 빼고 그 다음엔 그 값들의 표준편차를 구해서 그 표준편차를 나눠주면
• 이 값의 평균은 0이 되고 분산은 1로 된 것을 알 수 있음

• 즉, 이 과정은 원래 가지던 값들이 고유의 평균과 분산이 무슨 값이었든 간에 그 정보를 버리고 표준화된 평균과 분산인 0과 1로 만들어주는 이런 과정으로 해석할 수 있음

  

• 그 이후에는 이 각각의 값들에 affine transformation 이라고 불리는

  

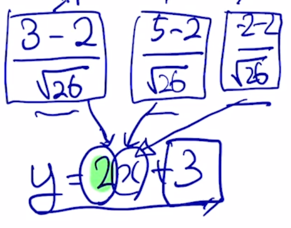
• 가령 $ y = 2x + 3 $ 이라는 연산을 수행하는 경우 이 값들이 각각의 $x$ 자리에 들어가서 해당하는 $y$ 값으로 변환이 되는데

• 이렇게 변환을 한 경우는 $x$ 의 평균과 분산이 0 과 1이었으면 그 결과 평균은 3이 되고 분산은 $2^2$ 즉 4가 되는 것을 알 수 있음

  

• 그리고 여기서 나오는 2 와 3은 뉴럴넷이 gradient descent 에 의해서 최적화를 하는 parameter 가 됨

  

• 그러면 뉴럴넷은 학습과정에서 이 특정 node 에서 발견되어야 하는 값에 가장 최적화된 평균과 분산을 원하는 만큼 가지도록 조절할 수 있는 방식으로 동작함

• 그러면 Layer Norm 도 Batch Norm 과 유사하게 첫번째 단계에서는 어떤 주어진 sample 들에 대한 평균과 분산을 0과 1로 만들고 그 다음엔 원하는 평균과 분산을 주입하는 그런 2단계로 이루어져 있음

  

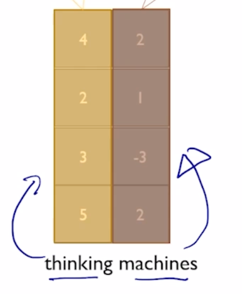
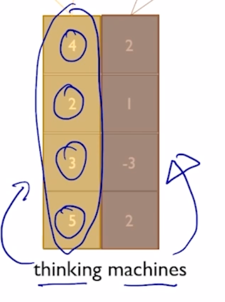
• 가령 “thinking”, “machines” 라고 주어진 두 단어로 이루어진 sequence 에 대해서 layer normalization 에 대한 이해를 설명하자면 해당하는 encoding vector 가 각각 4차원으로 나타나 있을 때

  

• 각 word 별로 특정 layer 에서 발견되는 이 4개의 node 들의 값들을 모아서 그 값들의 평균과 표준편차를 구하고 그 값을 각각 0과 1로 만들어주는 변환을 하게 됨

  

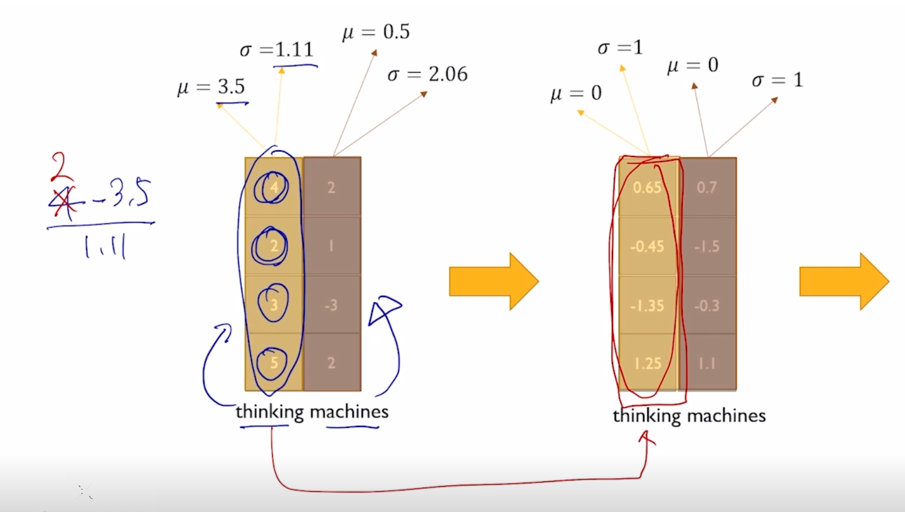
• 그러면 이 첫번째 값의 경우는 $\frac{4 - 3.5}{1.11}$ 이라는 연산을 수행하게 되고 2도 마찬가지로 4 자리에 2를 넣어서 동일한 변환을 수행한 다음에 얻어진 변환된 벡터는 이 특정 word 내에서 그리고 이 특정 layer 내에 4 dimension 으로 이루어지는 값이 평균이 0이고 분산이 1이 되도록 그렇게 통계값을 바꿔주었음

• 마찬가지로 두번째 단어에 대해서도 동일 연산을 단어의 평균과 분산으로 수행하게 됨

  

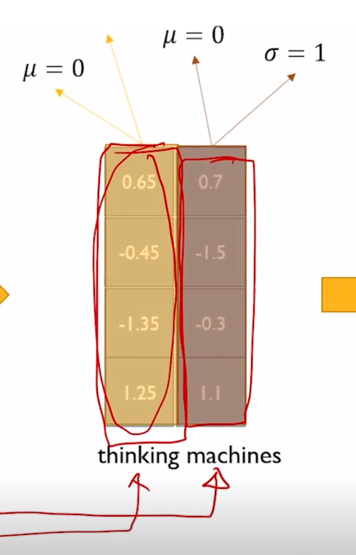
• 그렇게 변환된 평균이 각각 0이고 분산이 혹은 표준편차가 1이 되도록 단어별로 값을 조절했다면

  

• 다음에 2번째로 우리가 원하는 평균과 분산을 주입하기 위한 Affine transformation 즉, 쉽게는 $ y=ax+b $ 라는 연산을 수행을 할 때는 각각의 a, b 한 세트를 각 node 별로 여러 단어의 대해서 공통적인 변환을 적용해주게 됨

  

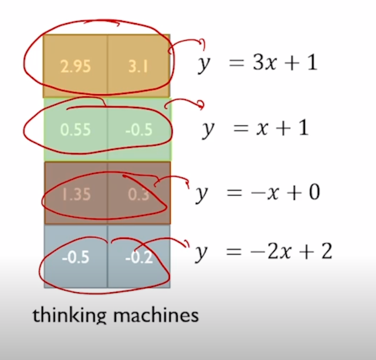
• 즉 column vector 를 기준으로 standardization 평균을 0, 분산을 1로 만들어주는 과정을 수행했다면 Affine transformation 은 이 layer 에서 발견된 각 node 별로 동일한 변환을 수행하게 됨

  

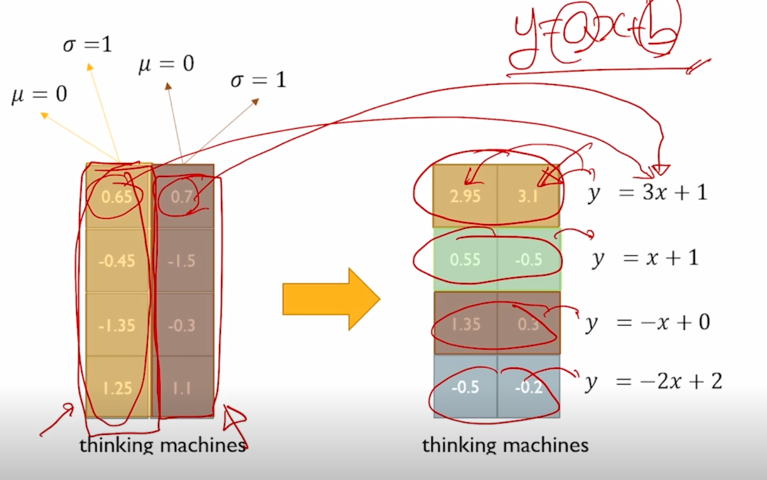
• 0.65 를 $ y = 3x + 1 $ 에 넣어서 나오는 값 2.95 를 넣어주고 0.7 을 $ y = 3x + 1 $ 에 넣어서 나오는 값 3.1 을 넣어주게 됨

• 이게 Layer normalization 이라고 불리는 방법이고 Batch Norm 과 세부적인 차이점은 비록 있지만 큰 틀에서는 학습을 안정화하고 최종적인 성능을 좀 더 끌어올리는데에 중요한 역할을 하는 것이 Layer Normalization 임

  

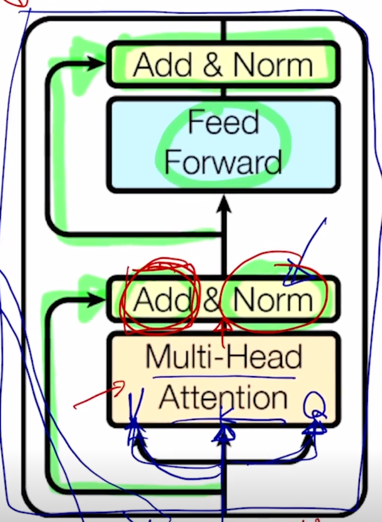
• 그래서 Transformer 에서 한 block 을 구성하는 Multi-Head Attention 및 residual connection 그리고 Layer Normalization 을 살펴봤음

• 그렇게 변환을 완료한 후에는 다시 word 별로 가지는 encoding vector 를 추가 적인 Fully Connected Layer 하나를 통과시켜서 각 word 의 encoding vector 를 변환하고 그 다음엔 또 동일하게 residual connection 을 통해서 output 과 더해주고 추가적으로 Layer Normalization 을 통해서 원하는 평균, 분산을 주입하는 방식으로 하나의 Transformer 에서 제안한 Self-Attention 모듈을 포함한 전체적인 하나의 block 이 정의가 됨

  

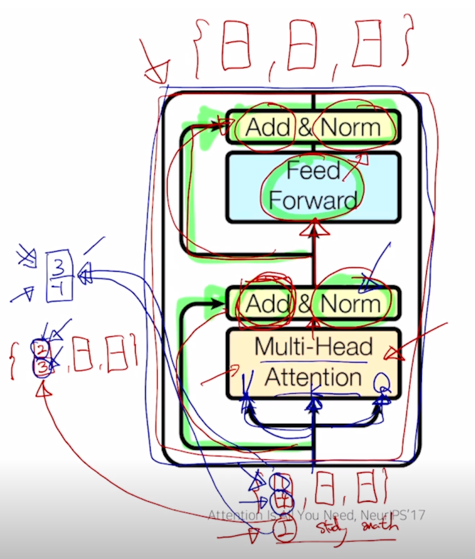
• 그렇지만 high-level 에서는 여전히 우리에게 주어진 sequence 가 “I study math” 각각의 단어에 대한 입력 벡터가 주어졌다면 residual connection 에 의해서 그리고 변하는 각각의 word 별 벡터에 적용되는 것이기 때문에 최종적으로 나오는 것은 동일한 차원을 가지는 2차원의 여전히 “I study math” 각각의 단어에 대응하는 encoding 벡터가 됨

Transformer: Positional Encoding

• 다음으로는 Transformer 모델이 가지는 또 다른 구성요소인 Positional Encoding 에 대해서 얘기해보자.

  

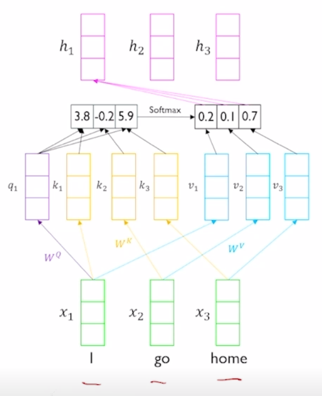
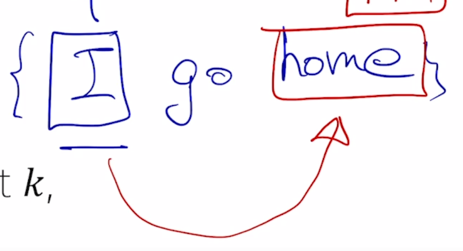
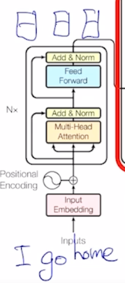
• RNN 과는 달리 self-attention 기반으로 주어진 sequence 를 encoding 하는 경우 가령 “I go home” 이라는 문장이 주어져 있으면

  

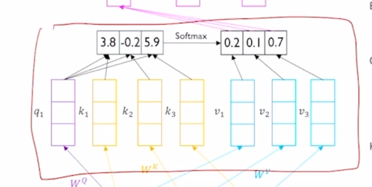
• 여기서 self-attention 모듈을 수행한 후

  

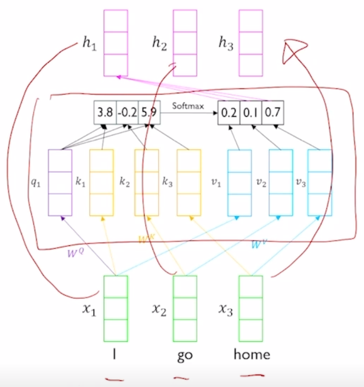
• 좀전의 말했던 전체의 block 을 다 수행한 이후 각 word 별 encoding vector 가 나오게 됨

  

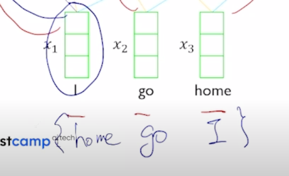
• 그런데 여기서 순서의 측면에서 “I go home” 이 아니라 가령 “home go I” 라는 순서로 encoding 을 했을 때를 생각해보자.

  

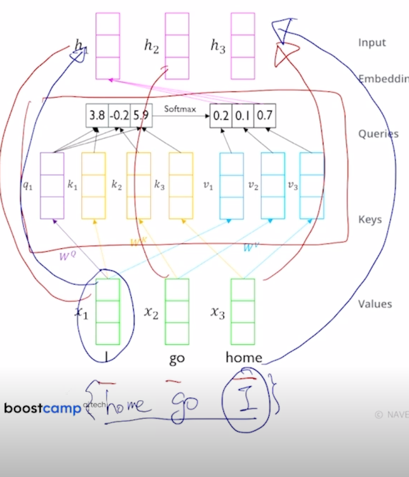
• 원래 순서에서 가지던 이 “I” 의 최종 encoding vector output 과 순서를 뒤집었을 때의 동일한 word “I” 에 해당하는 encoding vector output 은 동일하게 vector 결과가 나옴

• 이는 attention 모듈을 수행할 때 Key, Value pair 들은 순서에 전혀 상관없이 각 Key 별로 주어진 Query 와의 attention 유사도를 구하고 결국 그 해당 Value vector 의 가중치를 부여해서 가중합을 함으로써 주어진 Query vector 에 대한 Encoding vector 를 얻어내는데 주어진 가중평균을 낼 때에 이 Value vector 들이 당연히 교환법칙이 성립이 되기 때문에 최종 output vector 는 전혀 차이가 없이 첫번째 위치에 있었을 때나 세번째 위치에 있었을 때의 결과가 동일하게 됨

• 그러면 이러한 순서를 무시한다는 이 특성은 입력문장을 sequence 정보를 고려해서 encoding 을 하지 못하고 이것을 마치 순서를 고려하지 않는 집합으로 보고 각 집합에서의 원소의 encoding 을 얻는 과정으로 생각할 수 있음

  

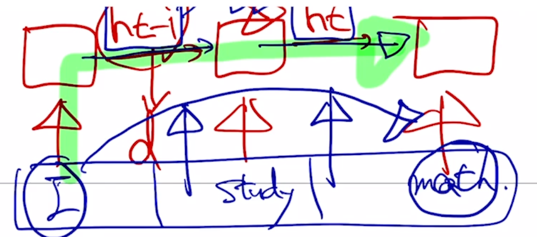
• 이 경우, RNN 과는 다른 차이점이 생기게 되는데 RNN 에서는 여기서 가령 이 3개의 단어가 이 특정한 순서가 아니라 이 순서가 바뀌어서 가령 “math study I” 가 되는 이런 방식으로 encoding 이 되면 각 word 에 대한 hidden state vector 는 당연히 순서가 달라지면 정보가 적층되는 순서가 달라지기 때문에 encoding vector 들도 달라지게 됨

• RNN 은 자연스럽게 sequence 를 인식하고 그를 구별해서 vector encoding 을 얻어낼 수 있는 기법이지만 Trnasformer 혹은 self-attention 모델은 그 순서정보를 반영할 수가 없는 그런 한계점을 가지게 됨

• 그래서 나오는 것이 Transformer 에서 쓰이는 Positional Encoding 임

  

• 가령 “I go home” 에서 “I” 가 가지는 입력 벡터가 3차원 벡터로서 [3 -2 4] 라는 벡터라고 생각하자.

• 그러면 입력벡터 “I” 에 해당하는 벡터를 이 “I” 라는 단어가 전체 sequence 에서 첫번째로 등장했다 혹은 첫번재 위치에 등장했다는 것을 이 벡터의 어떤 형태로 정보를 포함시켜줌

  

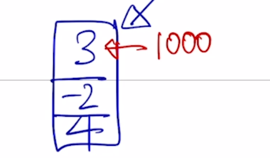
• 간단한 예는 첫번째 위치에서 발견된 word 인 경우 첫번째 dimension 에 1000 이라는 숫자를 더하는 것임

  

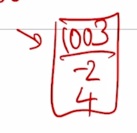
• 그러면 이 경우 이 벡터는 [1003 -2 4] 가 됨

  

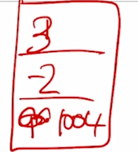
• 그랬는데 이 벡터가 가령 3번째 위치에 나타난 경우라면 두번째 세번째 dimension 에서 이 sequence 의 위치가 세번째인 경우 첫번째 dimension 이 아닌 세번째 dimension 에 1000을 더해주게 되면 그 해당 벡터는 [3 -2 1004] 가 됨

  

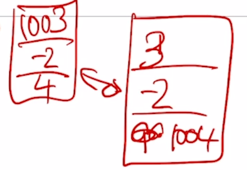
• 이 2개의 벡터는 명확하게 차이가 나게 되고 같은 입력벡터 시작했다고 하더라도 그 위치에 따라 서로 다른 값을 가지게 됨
• 즉, 여기서 핵심 아이디어는 각 순서를 규정할 수 있는 각 순서를 특정지을 수 있는 Unique 한 지문과도 같은 그래서 서로 다른 순서간의 구별이 되는 특정한 상수 벡터를 각 순서에 등장하는 word 입력 벡터에 더해주는 것임

• 이것을 Positonal Encoding 이라고 부름

• 그런데 이 더해주는 벡터를 어떻게 결정하느냐는 위에서 말한 simple 한 예로 하지는 않고 위치에 따라 구별할 수 있는 벡터를 $sin$ 과 $cos$ 등으로 이루어진 주기함수를 사용하고 그 주기를 서로 다른 주기를 써서 여러 $sin$ 함수를 만든 후 거기서 발생된 특정 $x$ 값에서의 함수값을 모아서 위치를 나타내는 벡터로 사용하게 됨

• Use sinusoidal functions of different frequencies

  

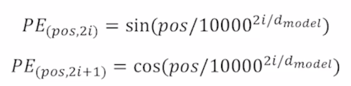
• 가령 각 dimension 별로 $sin$ 혹은 $cos$ 함수를 이렇게 만듦

• 가령 첫번째 dimension 에 해당하는 함수는 $sin$ 을 택하고 주기는 위치 정보에 따라 주기가 변하는 그런 형태의 함수를 가짐

• Easily learn to attend by relative position, since for any fixed offset $k$, $PE_{(pos+k)}$ can be represented as linear function of $PE_{(pos)}$

  

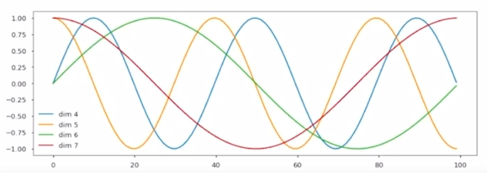
• 여기서는 1, 2, 3 번의 dimension 이 생략되고 4번째 dimension 을 예를 들면 4번째 dimension 은 $sin$ 그래프로 어떤 특정한 주기를 가지고 5번째 dimension 은 여기서는 $sin$, $cos$ 이 번갈아가면서 $cos$ 이 되고 $cos$ 에서의 특정 주기를 가지는 함수 그리고 6번째 dimension 에서는 또 이번엔 $sin$ 이 되고 아까의 $sin$ 그래프와는 주기가 다른 형태의 $sin$ 그래프를 얻어내게 됨
• 그러면 이렇게 dimension 개수만큼의 서로 다른 주기 그리고 $sin$ 혹으 $cos$ 이 번갈아가면서 그래프가 생성되는 이런 패턴을 만들어 놓은 후

• 첫번째 위치를 0 베이스의 index 로 삼아서 첫번째를 0번 인덱스라고 하면 0번 에서의 position encoding vector 입력 벡터에 더해주는 그 첫번째 위치를 나타내는 unique 한 지문과도 같은 그 벡터를 바로 4번째 dimension 에서는 파란색의 그래프에서 얻고 5번째는 주황색의 그래프에서 다섯번째 dimension 의 값을 얻는 식으로 dimension 개수만큼 $sin$ 혹은 $cos$ 그래프가 있기 때문에 첫번째 위치 혹은 position 을 나타내는 vector 를 $sin$ 혹은 $cos$ 으로 얻어내게 됨

  

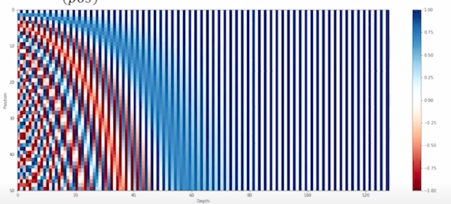
• 위 그림은 위의 방식을 통해 만들어진 $sin$, $cos$ 그래프를 통해 총 128 차원의 입력벡터를 기준으로 해서 만들어진 position encoding vector 를 나타내고 있음

  

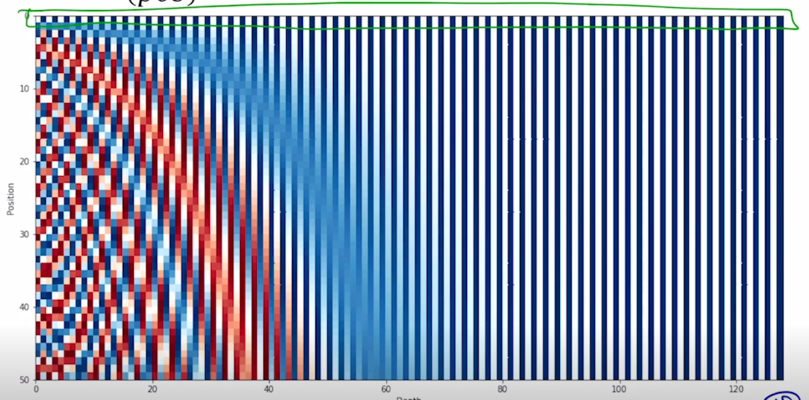
• 0번째 position 에서는 첫번째 row vector

  

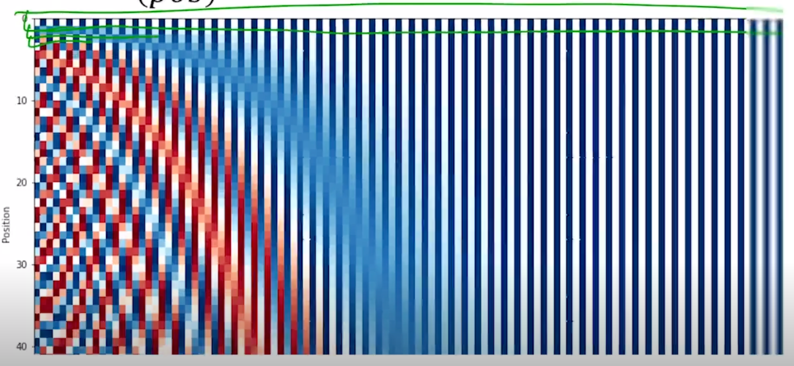
• 두번째 row vector 그리고 세번째 row vector 이렇게 이 행렬에서의 각각의 row vector 를 그 해당 postion encoding vector 로 사용하여 마치 위에서 [1000 0 0] 이라는 벡터를 넣어줬듯이 이 벡터 대신 여기 있는 해당 포지션의 row 번째의 벡터를 더하여 줌

• 이러한 방식에 따라 순서를 구별하지 못한다는 self-attention 모듈의 기본적인 한계점을 이렇게 위치별로 서로 다른 vector 가 더해지도록 함으로써 위치가 달라지면 결국 출력 encoding vector 도 달라지도록 하는 방식으로 그 순서라는 정보를 이 Transformer 모델이 다룰수 있도록 함

Transformer: Warm-up Learning Rate Scheduler

• 다음으로 Transforemr 모델에서 사용된 학습상에서의 learning rate scheduling 이라는 기법을 살펴보자.

• learning rate = $d_{model}^{-0.5} \cdot $ min(#$step^{-0.5}$, #$step \cdot warmup_steps^{-1.5}) $

• learning rate scheduling 은 일반적으로 gradient descent 및 그에 대한 다양한 좀 더 진보된 알고리즘인 Adam 등의 과정을 통해 최적화를 수행하는 과정에서 사용되는 learning rate 라는 하이퍼파라미터를 학습 전 과정동안 하나의 고정된 값으로서 사용을 하게 되는데 그렇지만 학습을 좀 더 빠르게 하고 최종 수렴하는 모델의 성능도 어느정도 고정된 값에서 하이퍼파라미터로서의 learning rate 를 썼을 때 보다 더 최종 수렴 모델의 성능을 올릴 수 있도록 하는 목적으로서 이 learning rate 값도 학습중에 적절히 변경해서 사용하게 되는 것이 learning rate scheulding 방식이라고 부름

  

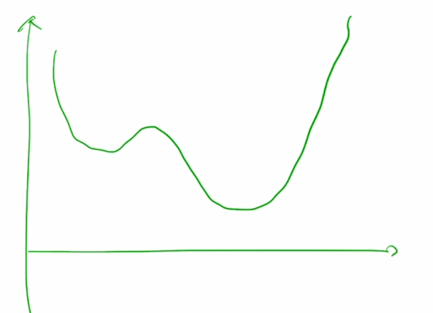
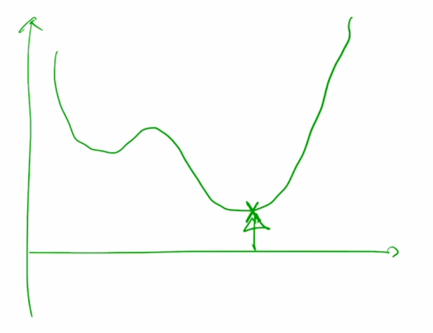
• objective function 이 최적화하고자 하는 파라미터에 대해서 이러한 식으로 그려져 있는 경우

  

• 여기서 가장 minimum 값에 해당하는 지점으로 도달하는 것이 gradient descent 에서 일어나는 일임

  

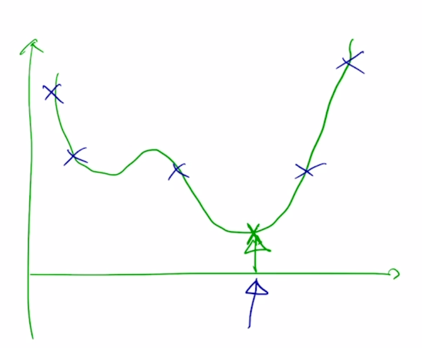
• 이 경우 최적화에 참여하는 파라미터 값을 랜덤하게 초기화를 하는데 도달하고자 하는 점과는 상대적으로 거리가 굉장히 먼 임의의 위치에서 시작을 할 가능성이 높음

  

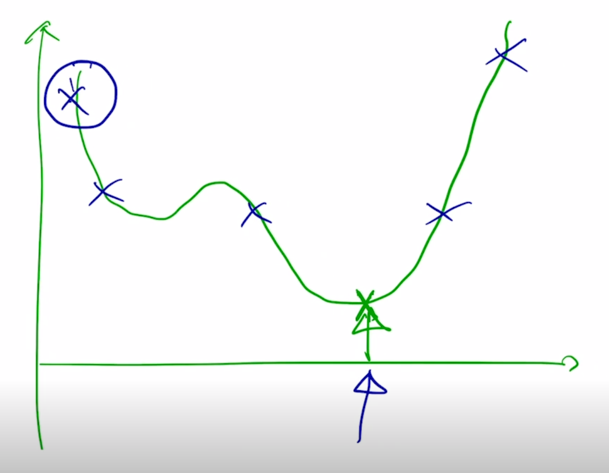
• 가령 가장 왼쪽에서 시작한 경우 이 경우는 아마도 objective function 의 형태를 보면 이 때의 gradient 값은 굉장히 가파른 곳에 위치해 있을 가능성이 높음

  

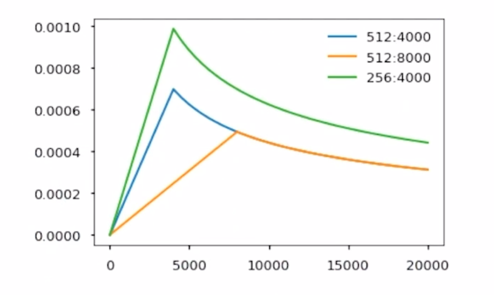
• 여기서 x 축이 iteration 숫자가 되고 그래서 초반에는 learning rate 를 굉장히 작은거로 사용을 하게 됨

• 작은 값을 사용해서 원래 해당 gradient 값이 클 때 적절하게 작은 learning rate 값이 곱해짐으로써 너무 큰 보폭이 발생되는 것을 방지함

  

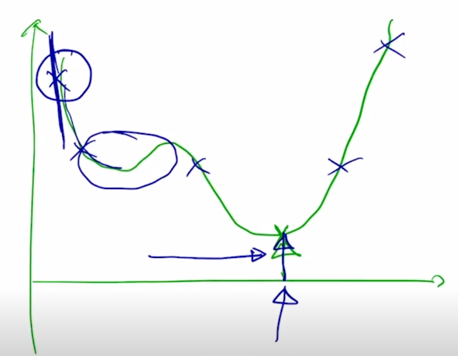
• 그러다가 어느 정도 iteration 이 진행되면 뭔가 완만한 구간에 도달할 수 있는데

  

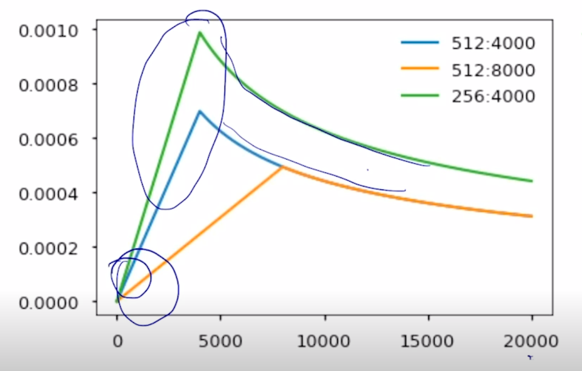
• 이 경우는 아직 우리가 도달해야 하는 optimal point 가 아직은 멀리 있을 수 있기 때문에 그래서 좀 더 동력을 주는 차원에서 점차로 learning rate 를 iteration 에 비례해서 올려주게 됨

  

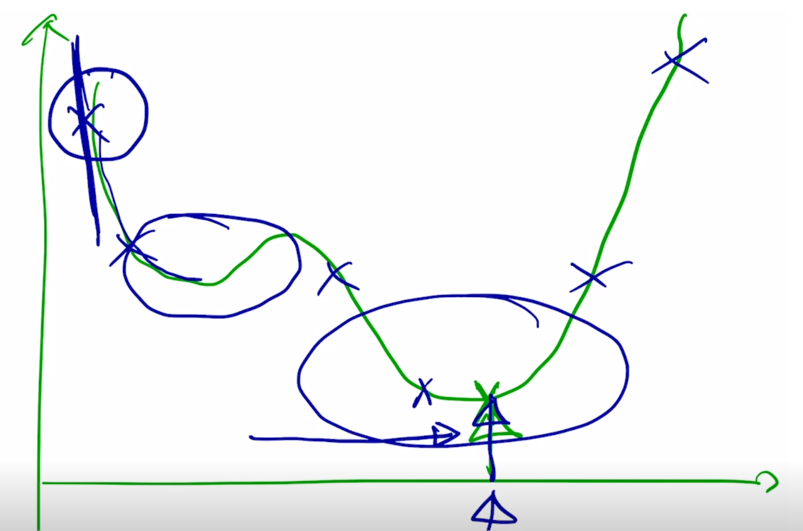
• 그 전에 큰 learning rate 를 통해서 빨리 왔다면 혹은 적은 iteration 을 통해 global minimum 바로 왼쪽에 도달한 경우라면

  

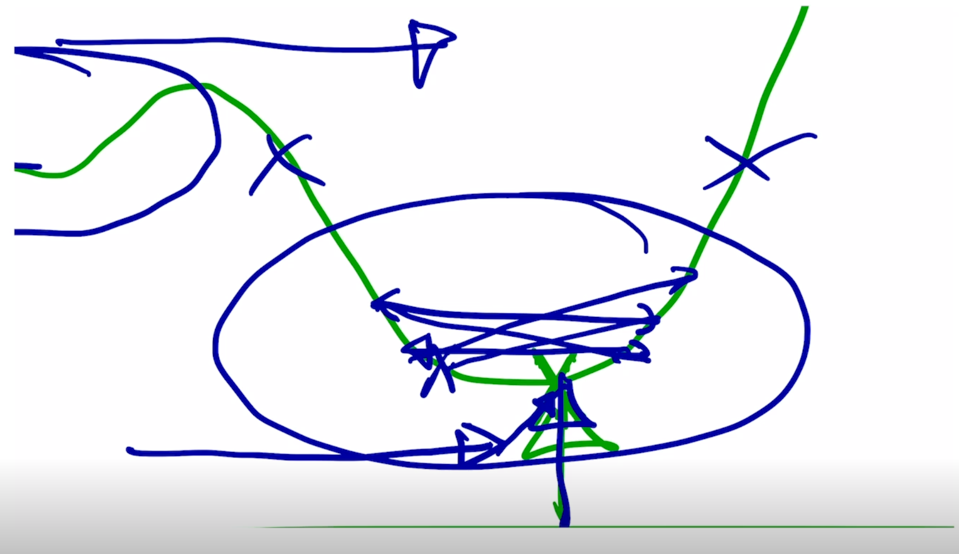
• 여기서는 learning rate 를 크게 쓰면 보폭이 큼으로 인해서 정확한 point 에 도달하지 못하고 그 주변을 맴도는 objective function 값을 낮출 수 있음에도 큰 learning rate 때문에 그러지 못하는 상황이 벌어짐

• 그래서 근처까지 다 온 이런 상황에서는 정확한 point 에 잘 도달할 수 있도록 learning rate 를 점차로 줄여주는 그런 형태로 learning rate 의 값을 iteration 이 진행됨에 따라 동적으로 바꿔 주게 됨

• 그래서 이러한 방식의 learning rate scheudling 을 사용했을 때 경험적으로 transformer 모델이 여러 task 에서 좀 더 좋은 성능을 내는 것이 알려져 있음

Transformer: High-Level View

• Transformer 모델에서 encoder 부분을 다 얘기했음

• Attention is all you need, NeurIPS’ 17
  • No more RNN or CNN modules

  

  

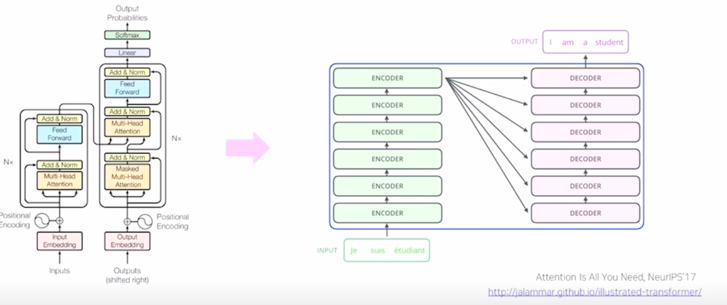
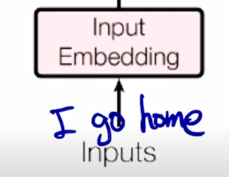
• 기본적으로 “I go home” 이라는 문장이 주어지는 경우 각각에 해당하는 embedding vector 를 입력으로 주고

  

• 각 position 별로 그 해당 poistional encoding vector 를 더해주고

  

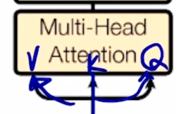
• 자기 자신 sequence 를 encoding 을 Multi-Head attention 을 통해서 하기 때문에 Value, Key, Query 의 동일한 vector set 를 입력으로 주고

  

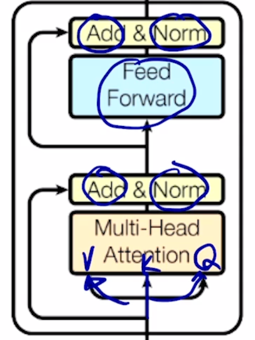
• 위에서 말했던 residual connection, layer normalization 그리고 추가적인 feed forward layer 그 다음에 또 residual connection 그리고 layer normalization 그래서 이 하나의 block 으로 이루어진 이 block 을 다 수행한 후에는

  

• “I go home” 에 대한 벡터가 2차원 벡터였으면 역시 또 sequence 길이와 동일한 개수의 vector 가 최종적인 encoding output 으로 나오게 됨

  

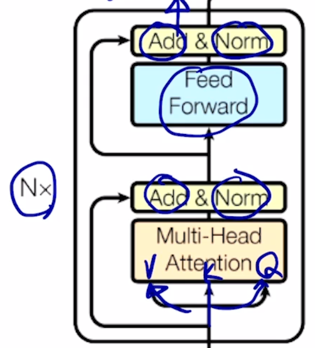
• 여기서 N x 라고 쓰여진 것이 있는데 이 encoding block 을 총 N 번 여기서 N 은 6, 12, 24 등의 값을 주로 사용

• 가령 6 인 경우 동일한 block 을 6번을 쌓아서 각 block 간에는 파라미터가 제각각 독립적인 파라미터를 가지게 됨

  

• 그러면 아까 encoding output 이 다시 동일한 encoding block 으로 들어가면서 sequence 의 각 word 에 해당하는 encoding vector 가 점차로 좀 더 high-level 의 vector 로 encoding 이 진행됨

  

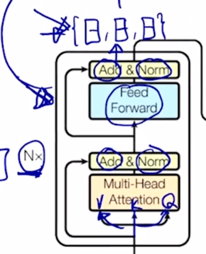
• 그렇게 해서 다 쌓고 나면 최종 마지막 layer 의 output 으로 나오는 각 word 별 encoding vector 를 얻게 됨
• 그래서 이게 encoding 과정의 전부가 됨

Transformer: Encoder Self-Attention Visualization

• 그러면 encoding 모듈이 하는 흥미로운 패턴을 살펴보면 어떤 특정한 encoding 당시의 layer 에서의 attention 모듈에서의 패턴을 보면 다음과 같음

• Words start to pay attention to other words in sensible ways

  

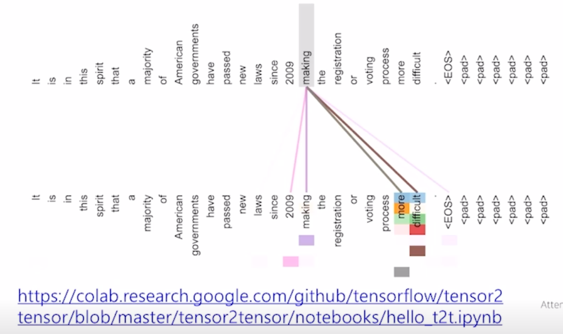
• 여기서 위쪽과 아래줄이 모두 동일한 문장인 것으로 보이고 그래서 주어진 각 word 의 입력 벡터가 attention 모듈을 한 번 수행하면서 나타나는 각 word 가 Query 로 사용됐을 때 이 주어진 입력 벡터들 Key 와 Value 벡터들을 사용해서 어떤 식으로 정보를 가져가는 것인지를 패턴을 보여줌

  

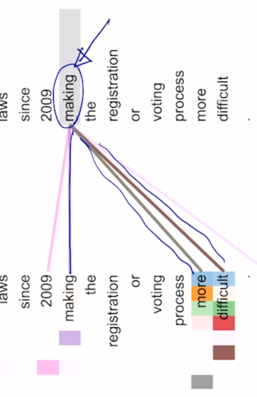
• making 이라는 Query 자격의 vector 가 자기 자신의 정보를 어느정도 가져가는 것을 알 수 있고 more, difficult 에 해당하는 정보를 많이 가져가는 것을 알 수 있음

• 그리고 동시에 since 다음에 2009 시기를 나타내는 making 이라는 어떤 형태의 action 이 언제 혹은 언제부터 일어났는지에 시기 정보를 가져가고 있는 것으로 보임

  

• 그 다음에는 화살표의 두께 그리고 색깔 뿐만 아니라 자세히 보면 같은 word 라고 하더라도 여러 grid 형태가 보여지는 것을 알 수 있음

  

• 여기서의 grid 는 각각 첫번째 부분이 첫번째 head 에서의 attention vector 를 의미하고 2번째 줄이 2번째 head 에서의 attention vector 를 의미

• 그래서 처음 4~5개 정도의 head 에서는 making 의 목적보어에 해당하는 more difficult 한 상황으로 만들었다 라는 이 부분을 주로 많이 attention 을 가하고 있으면서 그 정보를 가져가는 것을 알 수 있음

  

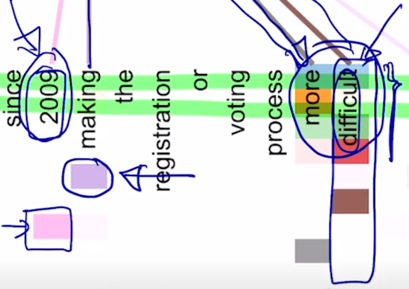
• 동시에 자기 자신을 attention 하는 특정 head 가 존재하고 역시 마찬가지로 2009 년 이라는 시기 정보를 주로 해당정보로 가져가고 있는 head 가 별도로 존재하는 것을 알 수 있음

  

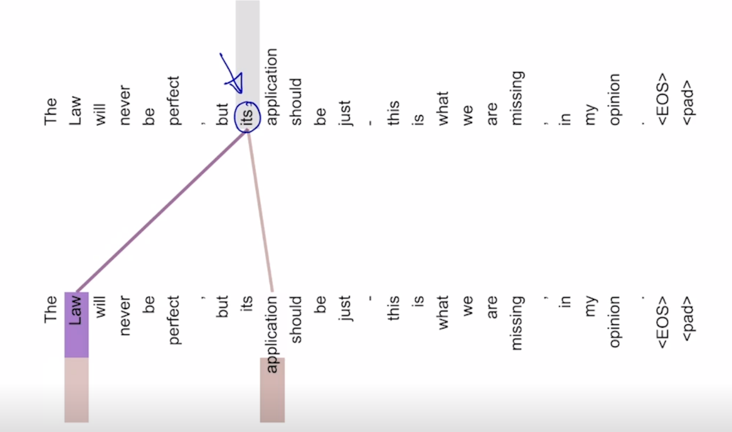
• 또 다른 단어를 Query 로 사용했을 때 attention 의 시각화 패턴을 보면 its 라는 단어에서 볼 때, 주로 Law 라는 단어 application 이라는 단어에 가령 첫번째 head 에서의 attention 은 Law 에 많은 가중치를 부여하고 있고 두번째에 대해서는 application 에 많은 가중치를 부여하는 것을 알 수 있음

• 그래서 첫번째 head 는 its 에서 it 이 가리키는 단어를 의미하는 것을 알 수 있음

• 두번째 head 에서의 application 은 its 가 한정해주는 그 해당 명사의 정보를 가져오는 것을 알 수 있음

• 이런 다양한 의미있는 패턴들이 보여지는 사례들이 있음
• 아래쪽에 있는 website 에 가시면 intearctive 하게 특정 layer 와 특정 head 그리고 특정 word 들을 Query 로 혹은 Key 로 사용했을 때 해당 attention 패턴이 동적으로 시각화되는 것을 볼 수 있음
• https://colab.research.google.com/github/tensorflow/tensor2tensor/blob/master/tensor2tensor/notebooks/hello_t2t.ipynb

Transformer: Decoder

• Two sub-layer changes in decoder

• Masked decoder self-attention on previously generated output

  

• Encoder-Decoder attention, where queries come from previous decoder layer and keys and values come from output of encoder

  

• 그 다음에는 Transformer 에서의 Decoder 부분을 살펴보자.

  

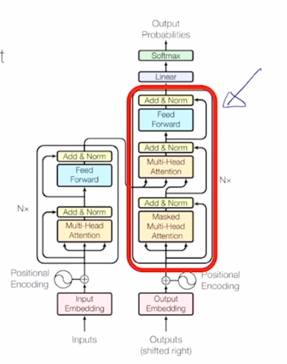
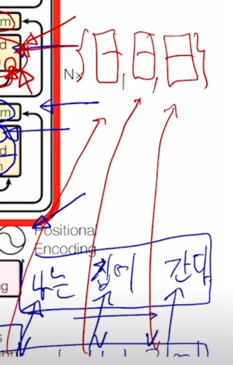
• 여기서 decoder 에서 “I go home” 이라는 문장이 주어졌을 때

  

• 이를 encoding 하고 그 다음에 이를 “나는 집에 간다” 라는 문장으로 번역하는 경우를 생각해보자.

  

• 그 경우 seq2seq with attention 모델을 학습한 과정을 살펴보면 처음에 우리가 주는 입력은 나는 집에 라는 단어가 학습 당시에 decoder 에 입력 sequence 로 주어지고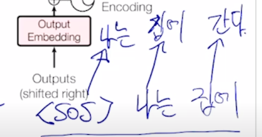

  

• 그 다음에 나오는 단어인 “나는 집에 간다” 라는 단어로 출력 word 가 예측 단어로서 나와야 함

• 그러면 decoder 상에서 원래 ground-truth 문장인 “나는 집에 간다” 그리고 이 부분을 오른쪽으로 한 칸 밀어서 “ 나는 집에" 라는 입력 sequence 를 각각의 embedding vector 로 주게 됨

  

• 그러면 이는 positional encoding 을 거친 후 그 다음엔 주어진 sequence 를 앞서 배운 Multi-Head attention 으로 encoding 을 한 후 그 다음엔 residual connection 그리고 layer normalization 을 거쳐서 주어진 이 output sequence 를 encoding 하는 과정을 거치게 됨

  

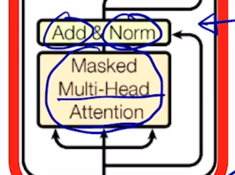
• 이 과정은 seq2seq with attention 모델에서 decoder 에서의 hidden state vector 를 뽑는 그 과정에 해당한다고 볼 수 있음

• 그런데 여기서 Masked 라는 추가 적인 단어가 들어가 있는 것을 알 수 있음

• 이 부분은 뒤에서 설명하기로 하고 위의 연산들에 대해서 더 살펴보자.

  

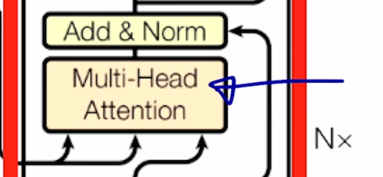
• 각각의 “ 나는 집에" 에 해당하는 encoding vector 가 decoder 의 hidden state vector 로 얻어졌다면 그 다음에는 다시 Multi-Head attention 에 입력으로 주는 것을 알 수 있음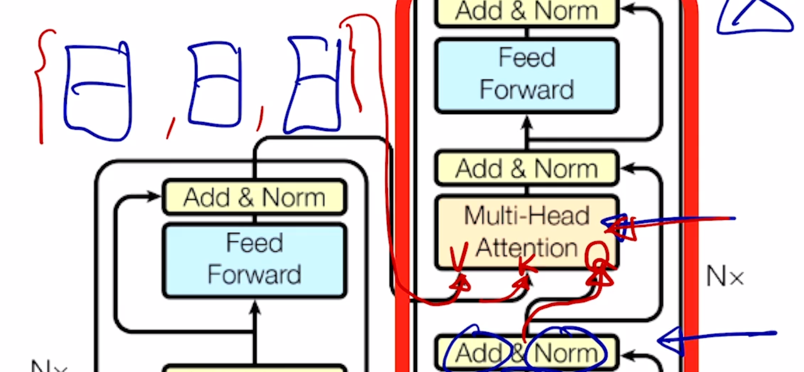

  

• 그렇지만 여기서는 Value, Key, Query 각각의 입력에 대해서 decoder 에서 만들어진 hidden state vector 가 Query 로 사용되고 encoding 단의 최종 출력 벡터가 Key 와 Value 로 들어가서 attention 이 수행됨

  

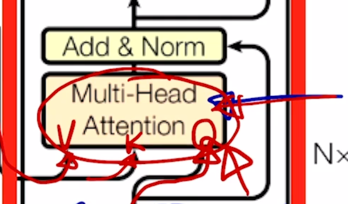
• 그러면 Multi-Head attention 이 부분이 seq2seq with attention 에서 추가적인 attention 모듈로서 여기에 들어가는 decoder hidden state vector 를 Query vector 로 해서 encoder 의 hidden state vector 중 어느 vector 를 가중치를 걸어서 해당 정보를 서로 다른 decoder 의 timestep 에서 가져올 지 그렇게 정보를 가져오는 encoder-decoder 간의 attention 모듈이 이 부분에 해당

  

• 그 이후에는 다시 residual connection 과 layer normalization 을 통해 그리고 추가적으로 feed forward layer 그 다음엔 residual connection 그리고 layer normalization 을 통해 “ 나는 집에" 에 해당하는 각각의 vector 가 decoder 의 최종 encoding vector 로서 나오게 됨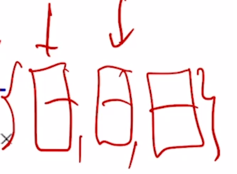

  

• 그러면 이 각각의 정보는

  

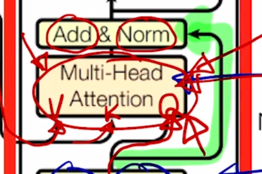
• 초록색 줄인 residual connection 에 의해서 decoder 의 문장에 대한 정보를 가지고 있음과 동시에

  

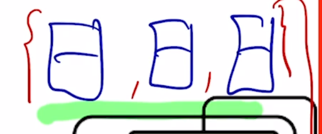
• encoder 에서 주어진 이 3개의 vector 에 대한 정보를 각각의 decoder 에 해당하는 매 timestep 마다 다른 정보를 가져와서 그 정보를 잘 결합한 vector 가 됨

  

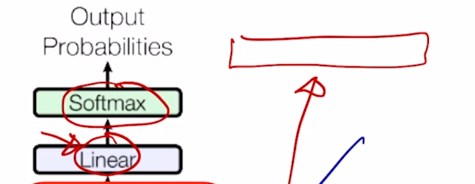
• 그러면 최종적으로 각각의 vector 에 linear transformation 을 걸어서 target language 에 해당하는 vocabulary size 만큼의 vector 를 생성
• 가령 한글 언어에서 vocabulary size 가 총 10만개가 있다고 하면 10만개의 vector 로 2차원의 vector 를 변환해주는 linear transformation 을 거친 후 거기에 softmax 를 취하고 특정한 한글 word 에 대한 확률값을 뽑아서 다음 word 즉, 첫번째에서는 “나는” 두번째에서는 “집에” 세번째에서는 “간다” 라는 단어에 대한 예측을 수해

• 그렇게 해서 나오는 한글단어의 대한 확률분포는 ground-truth 단어와의 softmax 를 통해서 backpropagataion 에 의해서 이 전체 네트워크가 학습이 진행됨

  

• 그러면 이제 Masked decoder 내에서 쓰이는 해당하는 부분에 대해서 알아보자.

Transformer: Masked Self-Attention

• Those words not yet generated cannot be accessed during the inference time

• Renormalization of softmax output prevents the model from accessing ungenerated words

  

  

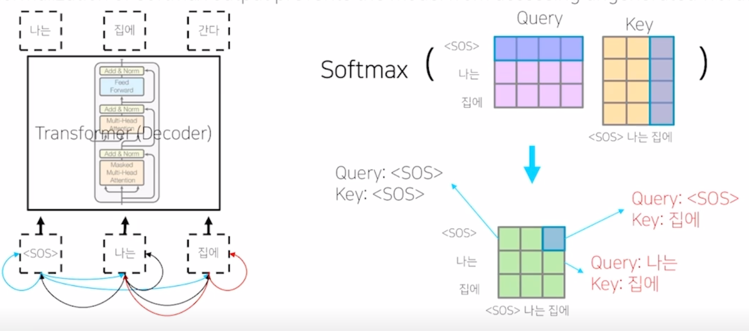
• Masked Self-Attention 의 기본 아이디어는 decoding 과정 중에 입력으로서 “ 나는 집에" 라는 단어들을 주고 다음 단어를 예측하는 과정에서 주어진 sequence 에 대해서 self-attention 을 통해 sequence 의 각 word 를 encoding 하는 과정에서 정보의 접근에 가능여부와 관련이 됨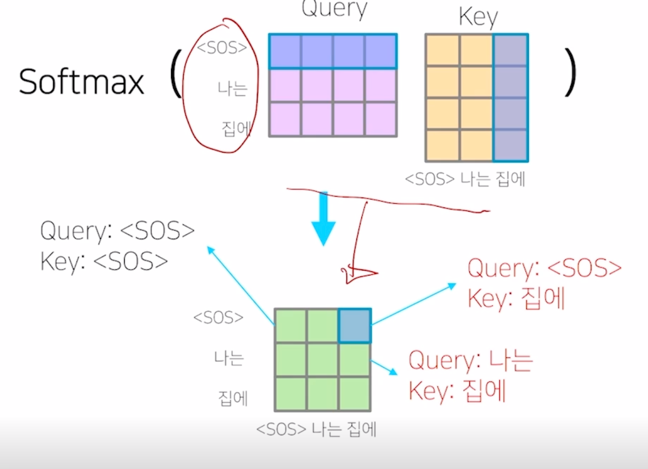

  

• “ 나는 집에" 라는 단어에 대해서 이를 Query 및 Key, Value 로 사용하는 self-attention 모듈을 수행하는 경우 이 Query, Key 에 해당하는 $QK^T$ 를 계산하게 되면

• 이 경우, “" 를 Query 로 했을 때 자기 자신 "" Key 를 얼마정도 유사도로 볼 지 그리고 "" 를 Query 로 했을 때, "나는" 에 해당하는 단어를 얼마정도의 유사도 혹은 "집에" 에 해당하는 단어를 어느정도의 유사도로 볼지를 결정해 주는 그런 정보를 담고 있음

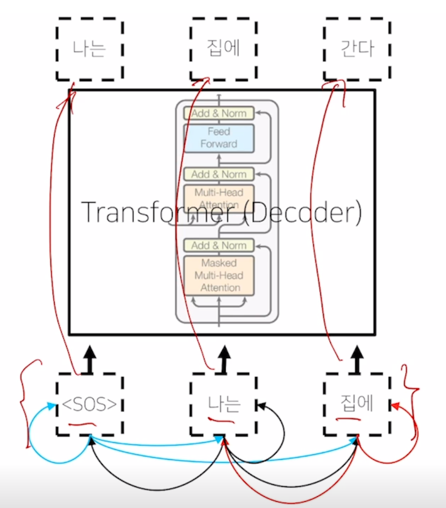
• 그런데 이렇게 해서 각 단어가 나머지 모든 단어들에 대해서 정보를 다 접근을 허용하게 되면 “" 라는 단어까지만 첫번째 timestep 에서 주어졌을 때 이 경우 물론 학습데이터에서 입력으로 주어야 하는 단어들이 "나는" 과 "집에" 라는 단어들이 주어져야 하는 것을 알지만 예측과정을 생각해보면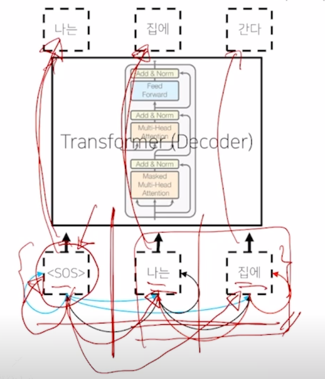

  

• “" 만 주어져있고 거기서 "나는" 이라는 단어를 예측해야 하고 " 나는" 까지의 단어가 주어져있을 때 "집에" 라는 단어를 예측하는 즉, 뒤에 나오는 단어를 학습 당시에는 배치 프로세싱을 위해서 입력으로 동시에 주긴 하나 이 "" 를 Query 로 사용해서 attention 모듈을 수행할 때는 접근 가능한 Key, Value 에서 "나는" 과 "집에" 라는 단어는 제외해 주어야 함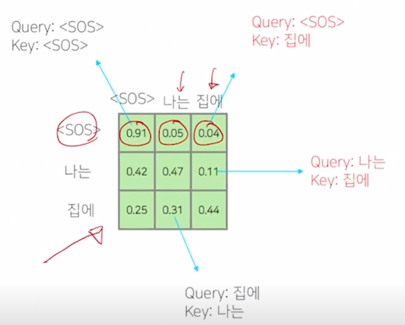

  

• 그렇게 되면 softmax 이후에 확률값이 계산이 된 이후에는 결국 “" 가 자기자신에 91% 두번째, 세번째로 나타나는 단어를 근소하지만 작은 확률로 본다고 할 때, 여기서 정보를 가져올 수 있는 것은 차단해주어야 함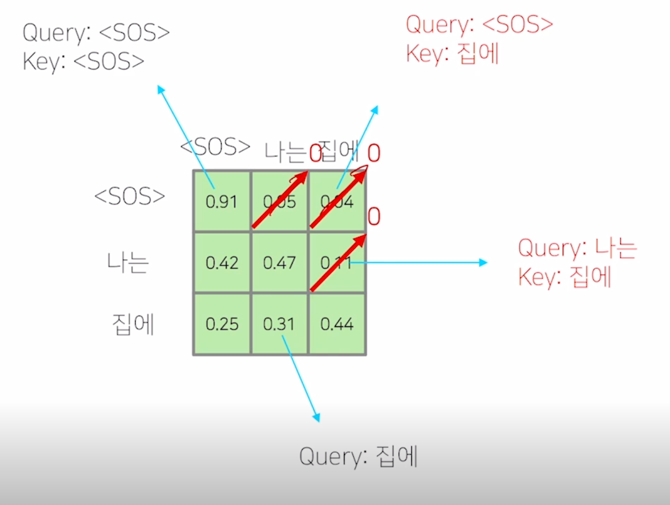

  

• 그래서 softmax 까지 구한 다음에는 이 값을 다 0으로 후처리 적으로 만들어 주게 됨

  

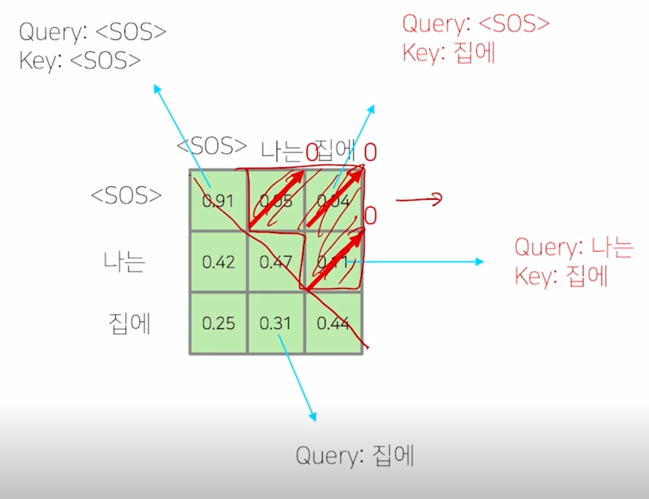
• 그 다음엔 이 softmax 에서 일부 (대각선 라인을 기준으로 윗부분에 해당하는 정보)를 모두 다 0으로 만들어주는 과정을 수행하게 됨)

• 그 다음엔 다시 row 별로 합이 1이 되도록 normalize 를 하게

  

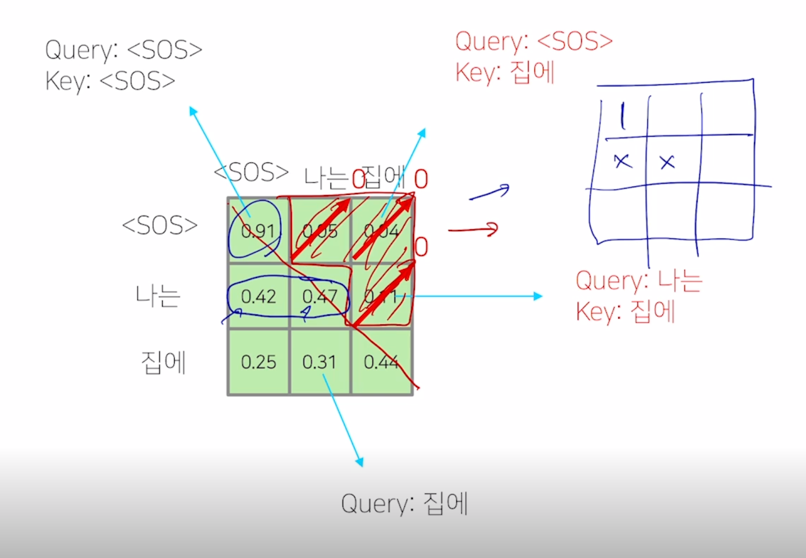
• 그래서 첫번째 row 에서 0.91 이 합을 0.91 로 나눠서 1이 되고 그리고 두번째 row 에서 0.42, 0.47 이 두 값을 합해서 그 값으로 각각의 값을 나눠주는 식으로 두개의 값의 합이 1이 되어서 주어진 Value vector 에 대한 가중평균 형태가 되도록 하는 방식으로 추가적인 후처리를 진행해주게 됨

  

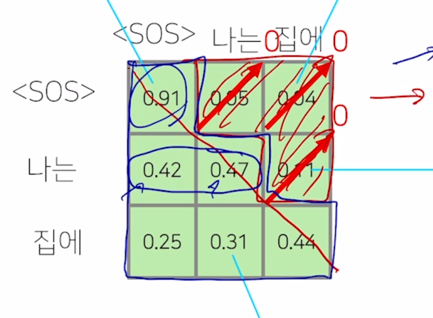
• 그래서 Masked self-attention 의 masking 이라는 의미는 여기서 보이는 것처럼 attention 을 모두가 모두를 볼 수 있도록 허용한 후 후처리 적으로 보지 말아야 하는 뒤에서 부터 나오는 단어에 대한 attention 의 가중치를 0으로 만들어주고 그 이후 Value vector 와 가중평균을 내는 방식으로 attention 을 변형한 그런 방식이 decoder 에서 사용되는 masked self-attention 이 됨

Transformer: Experimental Results

• Results on English-German/French translation (newstest2014)

  

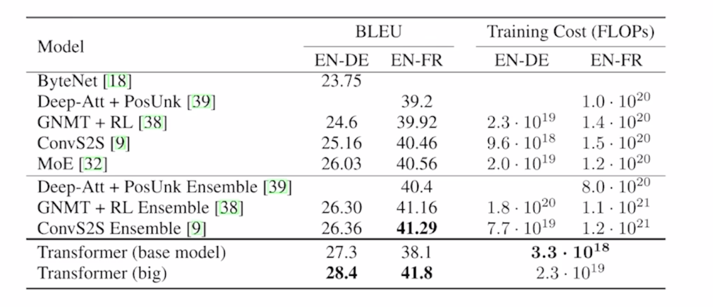
• 최종적으로는 자연어처리에서 가장 활발하게 연구되고 있는 기계번역 분야의 Transformer 라는 모델이 처음 제안 됐고 기계번역 분야는 굉장히 많은 사람들이 오랫동안 연구해왔던 그래서 최근까지 성능을 조금이라도 더 올리는데에 만만치 않은 그런 Task 였는데 Transformer 모델이 나오면서 기존의 가장 좋은 성능을 내던 seq2seq with attention 이러한 방법들을 일반적으로 성능을 더 올려준 결과를 내게 됨
• 여기서의 성능 measure 는 BLEU score 그리고 가령 학습 때 걸리는 계산량이나 시간등을 보여주고 있음
• BLEU score 는 앞서 배운 precision 을 기반으로 한 score 가 되고 transformer 기반의 모델이 가장 좋은 성능을 내는 것을 알 수 있음
• 여기서 BLEU score 값들의 경우 대략 20~40% 정도의 값을 가지는데 이 경우에는 BLEU score 의 최대 값이 100% 라는 것을 감안하면 번역성능이 대략 26% 40% 정도에 머문다는 것을 알 수 있음
• 그렇지만 보기보다는 훨씬 더 좋은 성능을 내는 결과에 해당이 됨
• 가령 “나는 수학을 열심히 공부한다” 라는 문장이 ground-truth 문장이고 “나는 열심히 수학을 공부한다” 라는 번역문장이 예측값으로 주어지는 경우에는 이 두 문장이 동일한 문장이긴 해도 2-gram, 3-gram, 4-gram 을 따졌을 때는 해당 precision 값은 굉장히 낮아짐
• 그래서 미처 50%가 안되는 BLEU score 라고 하더라도 실질적으로는 체감하는 번역성능은 실제로 google translate 나 네이버 파파고 등의 상용화된 기계번역 서비스에 필적하는 그런 정도의 성능이 됨