Day_30 01. Transformer (1)

Transformer (1)

Transformer: High-level view

• Attention is all you need, NeurIPS’17
  • No more RNN or CNN modules

  

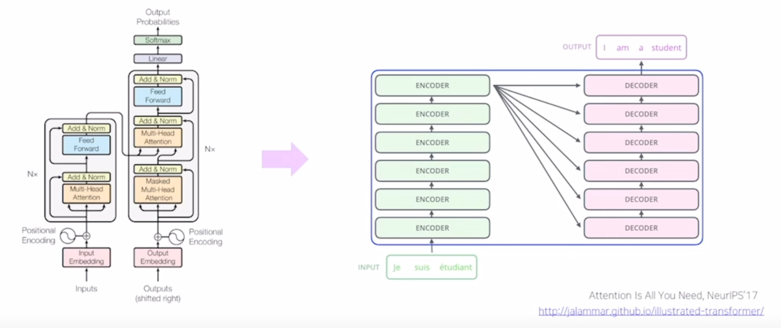
• Transformer 모델은 논문제목이 애초에 Attention is all you need 라는 논문이름으로 제안
• attention 이라는 모듈은 이전에는 LSTM 이나 GRU 기반의 seq2seq 모델의 추가적인 add one 모듈로서 attention 모듈이 사용되었다면 아예 sequence 데이터를 입력 혹은 출력으로 처리할 때 필요로하는 LSTM 이나 GRU 혹은 전반적인 RNN 모델 자체를 전에는 어떤 add one 모듈로서만 사용되던 attention 만을 사용해서 이 RNN 을 통채로 걷어내고 대체할 수 있다라는 그런 뜻을 가지고 있음
• 순수하게 attention 만으로 sequence 데이터를 입력으로 받고 또 sequence 형태의 데이터를 예측할 수 있는 모델구조

RNN: Long-term dependency

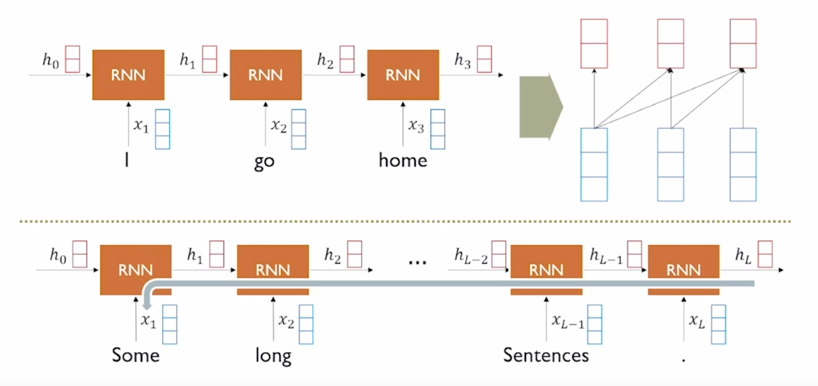
• RNN 구조를 통해서 sequence 데이터를 매 timestep 마다 인코딩하는 과정을 다시한번 살펴보자.

  

• “I go home” 이라는 문장이 주어졌을 때, 각 timestep 에서 RNN 모듈은 $x_t$ 와 $h_{t-1}$ 을 받아서 매 timestep 마다 그때그때의 $h_t$ 를 만들어내고 RNN 의 방향으로 보면 왼쪽의 단어서부터 오른쪽의 나오는 또는 그 이후에 등장하는 단어들에 대해서 이 정보를 계속적으로 축적해가면서 $h_1$, $h_2$ 등의 hidden state vector 를 인코딩하게 됨

  

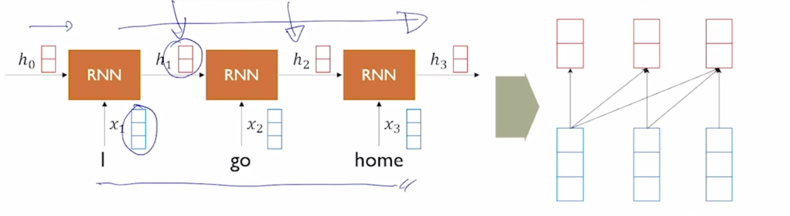
• 그러면 attention 을 사용했을 때, encoder level 에서 각각의 입력 word 에 대한 해당 timestep 의 hidden state vector 가 해당하는 timestep 의 각 word(“I”, “go”, “home”)를 적절하게 인코딩한 형태의 vector 로서 attention 의 재료로서 사용됨

  

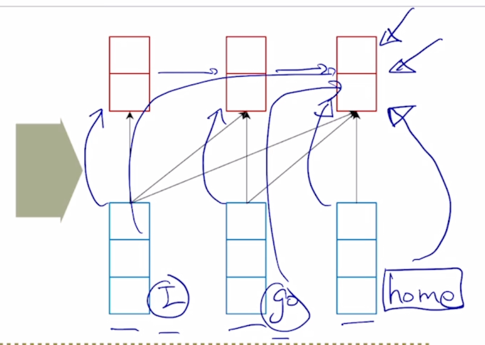
• “home” 의 경우는 마지막 timestep 에서 그때 당시에 들어온 입력단어인 “home” 이라는 정보를 주된 재료로서 encoding 을 하고있지만 그 연결관계를 입력으로 주어진 2개의 나머지 단어와 같이 생각을 해볼때에는 이런 RNN 의 계산 과정을 통해서 그리고 hidden state vector 의 흐름을 통해 “I” 라는 정보는 파란 화살표방향으로 그리고 “go” 라는 정보도 파란 화살표방향으로 “home” 이라는 encoding hidden state vector 에 담겨지는 것을 알 수 있음

  

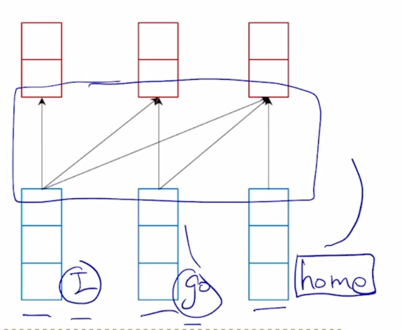
• 그러면 정보가 어디서 어디로 담겨져 있는가의 dependency 를 화살표 관계로 나타내면 파란박스로 나타낼 수 있음

• 그러면 3번째 timestep 에서의 “home” 이라는 단어가 멀리 떨어진 “I” 라는 단어를 적절히 포함하고 있으려면 그 “I” 로부터의 정보는 RNN 을 timestep 개수만큼 통과를해서 그 정보가 전달이 되게 되고 이경우 앞서 설명했던 gradient vanishing, exploding 혹은 Long-term dependency 이런 issue 에서 처럼 멀리 있는 timestep 에서의 정보를 배달을 해주기까지는 여러가지 정보의 손실, 유실, 혹은 변질 등의 issue 가 RNN 을 어쩔수없이 여러번의 걸쳐서 통과하게 됨으로써 일어날 수 있음

Bi-Directional RNNs

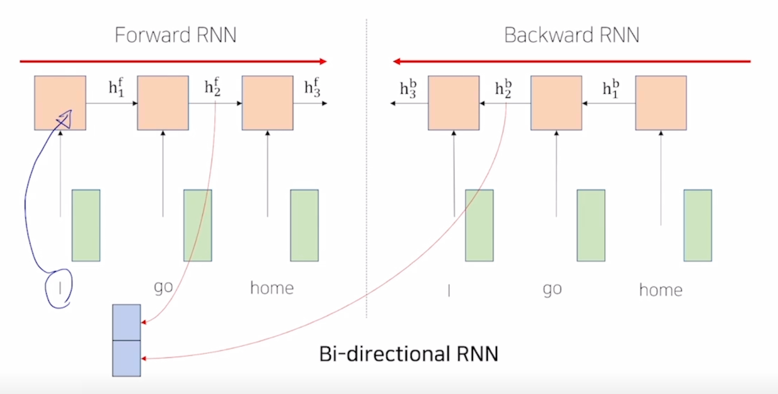
• 그러면 앞서 봤던 RNN 의 경우는 항상 그 정보가 왼쪽에서 오른쪽으로 흘러가는 왼쪽에서 나타나는 단어에서는 오른쪽에서 등장하는 단어의 정보를 참조해서 필요한 정보가 있다면 그 정보를 “I” 에 해당하는 encoding vector 에 담을수는 없게됨

• 이는 왼쪽에서 오른쪽으로 주어진 sequence 를 encoding 한 우리가 사용한 RNN 모듈의 특성 때문

  

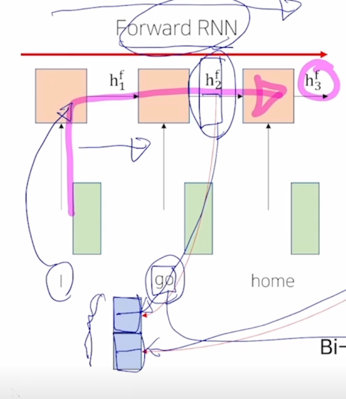
• 그런데 정보의 진행방향 혹은 sequence 의 방향을 왼쪽에서 오른쪽을 Forward RNN 이라고 할 때, 주어진 동일한 sequence 에 대해서 정보를 오른쪽에서 왼쪽으로 encoding 을 하는 이런 방식도 생각할 수 있음
• 그러면 여기서는 보통 Forward RNN 에서 사용되는 모델 혹은 모듈의 파라미터와는 다른 별개의 파라미터를 독립적으로 가지는 또다른 RNN 을 구성하게 됨

• 여기서 방향이 오른쪽에서 왼쪽으로 정보가 흐르는 방향이기 때문에 이를 Backward RNN 이라고 부름

  

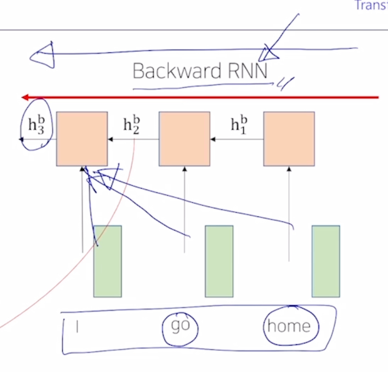
• 그러면 여기서는 “I” 에 대한 hidden state vector 는 결국 오른쪽에서부터 주어진 단어였던 “home” 그리고 “go” 에 해당하는 그런 정보들을 담을 수 있게됨

  

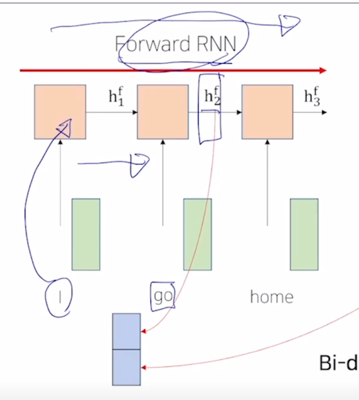
• 그러면 “go” 라는 단어의 경우 Forward RNN 에서는 “go” 의 왼쪽에 등장했던 단어들의 정보까지를 encoding 한 그런 hidden state vector 를 만들어낼수 있음

• 그걸 2차원 벡터라고 하겠음

  

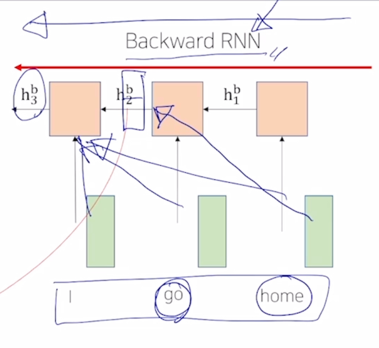
• 그다음 Backward RNN 에서는 “go” 라는 단어에 해당하는 hidden state vector 는 오른쪽에 등장했던 단어 “home” 의 정보를 포함한 vector 로 생각 할 수 있음

  

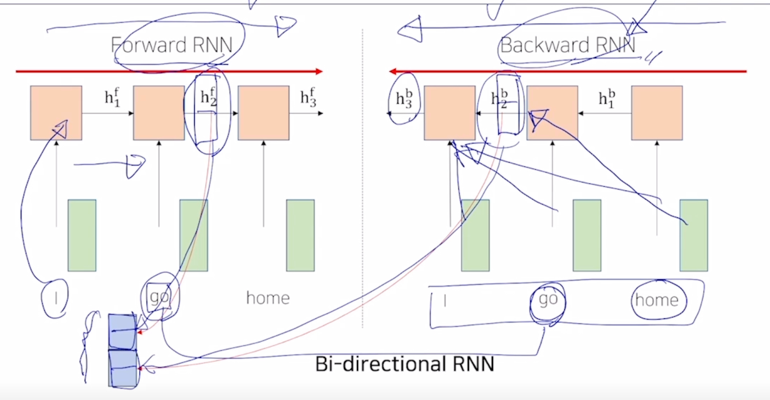
• 그러면 우리는 단어별로 encoding vector 를 구할 때 encoding vector 가 항상 왼쪽에 있는 정보 뿐만 아니라 오른쪽에 있는 정보도 같이 포함할 수 있도록 Forward RNN 과 Backward RNN 이 2개의 모듈을 병렬적으로 만들고 거기서 나타난 특정한 timestep 의 hidden state vector 가령 “go” 라는 동일 단어에 대해서 Forward RNN 에서 만들어진 hidden state vector 를 가져오고 Backward RNN 에서 만들어진 hidden state vector 를 가져와서 이 두 vector 를 concat 해줌으로써 hidden state vector 의 dimension 에 2배의 해당하는 vector 를 이 “go” 가 가지는 sequence 전체적으로 정보를 반영해서 encoding 한 vector 라고 볼 수 있음

Transformer: Long-Term Dependency

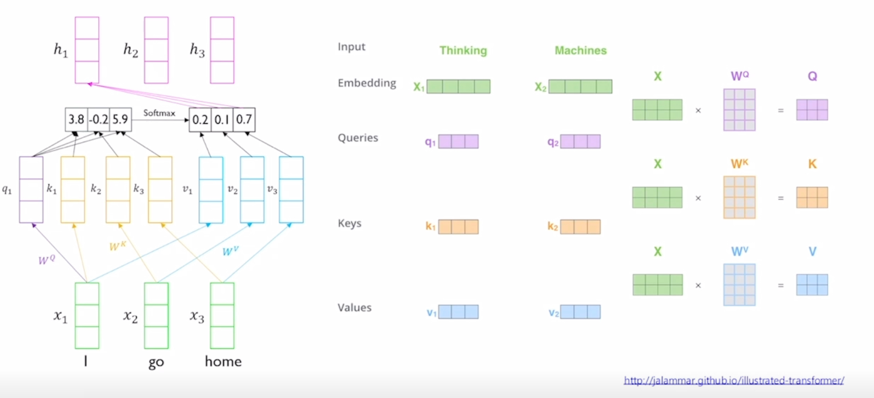
• 주어진 sequence 에 대해서 각 단어별로 이러한 전체 sequence 내의 문맥을 잘 반영한 encoding vector 를 단어별로 만들어내는 RNN 모델을 대체하는 용도로서의 Transformer 에서의 attention 모듈의 구조와 작동방식을 알아보도록 하자

  

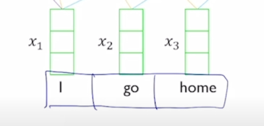
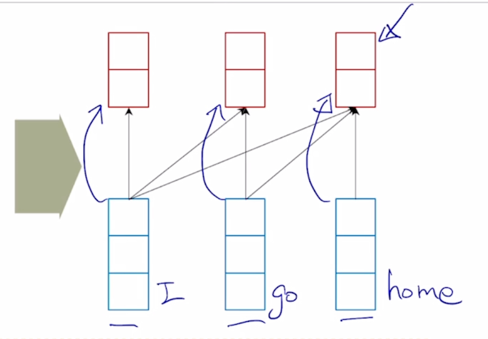
• “I go home” 이라는 동일한 세 단어로 이루어진 sequence 가 주어졌다고 할 때

  

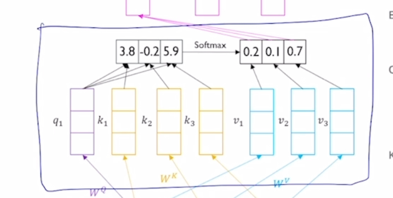
• 이 부분을 attention module 로서 본다면

  

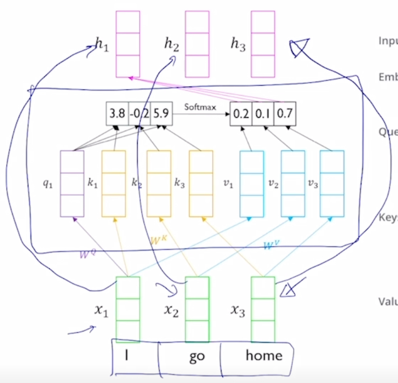
• 결국 이 입력 세 단어에 대한 input vector 가 주어진다면 출력으로서 나오는 이 vector 들은 역시 input sequence 에서 주어진 각 단어들로 sequence 전체 내용을 잘 반영하고 encoding 한 encoding vector 가 output 으로 나오게 됨

• 이런 측면에서는 RNN 에서 주어진 sequence 내의 각 word 들이 sequence 주변의 발견되는 정보를 발견해서 encoding 한 vector 를 역시 단어별로 생성해주는 것처럼 attention 모델에서도 입력과 출력의 setting 은 동일하게 유지된다는 것을 알 수 있음

• 그러면 구체적으로 어떤 방식으로 attention 을 적용해서 각각의 단어를 sequence 전체 내용을 보고 encoding 한 vector 를 만들어내는지를 알아보도록 하자

• attention 이 적용되는 방식은 앞서 배운 seq2seq with attention 에서 사용되는 방식과 거의 동일함

  

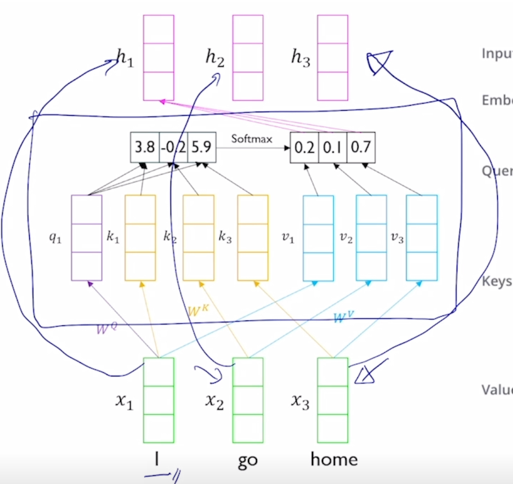
• “I” 라는 단어에 대한 encoding vector 를 만든다고 하면 “I” 에 대한 input vector 가 seq2seq with attention 에서 decoder 에서의 어떤 특정 timestep 의 hidden state vector 처럼 역할을 해서 이 vector 가 우리가 찾고자 하는 정보를 나타내고 있는 vector 가 되고 그 다음에 encoder 단에서 만들어진 hidden state vector 들의 set 가 주어져있을 때 각각의 vector 와 내적을 수행해서 유사도를 구하고 거기에 softmax 를 취해서 합이 1인 형태의 확률값을 만들어 준 후 그걸 가지고 다시 encoding vector 의 가중치로 부여를 해서 가중평균을 내는 방식으로 최종적인 attention module 의 output vector 혹은 context vector 를 계산했음

  

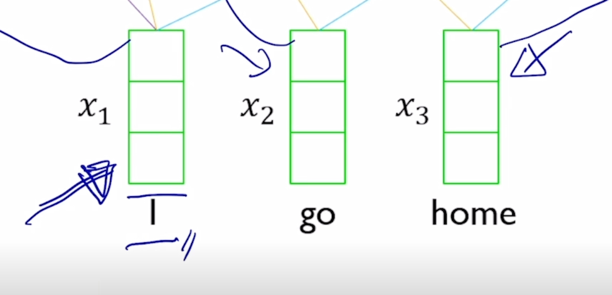
• 그러면 그 과정을 동일한 sequence 에 대해서 적용을 해보면 decoder timestep 의 hidden state vector 라고 생각을 할 때

  

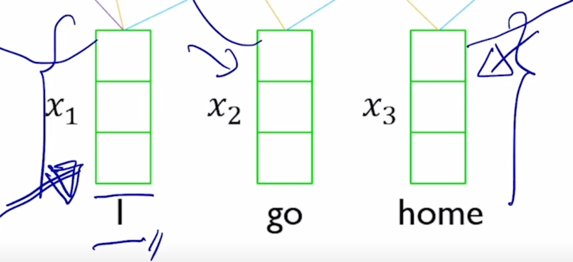
• encoder hidden state vector 의 set 는 3개의 vector 가 동일하게 사용되는 상황이 됨

  

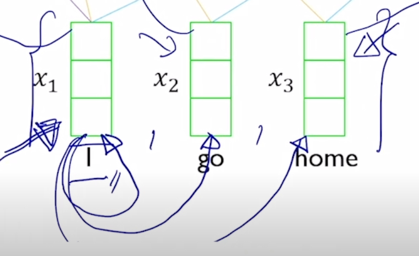
• 그러면 결국 “I” vector 가 자기 자신과 내적이 한번 되고 2번째, 3번째 vector 와 내적이 됨으로써 주어진 3개의 vector 와의 내적의 기반한 유사도를 구하게 됨

  

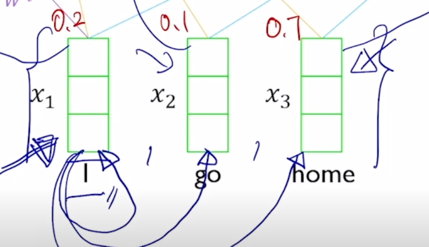
• 그러면 가령 거기서 나타난 내적의 기반한 유사도를 softmax 를 취해서 얻어진 가중치가 [0.2, 0.1, 0.7] 로 구성되었다면

  

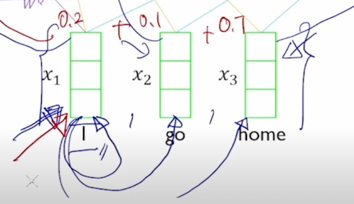
• 그러면 이 3개의 vector 에 해당 가중치를 걸어서 입력 vector 에 대한 선형결합 혹은 가중평균을 주어진 “I” 에 대한 word 의 encoding vector 로 생각할 수 있음

  

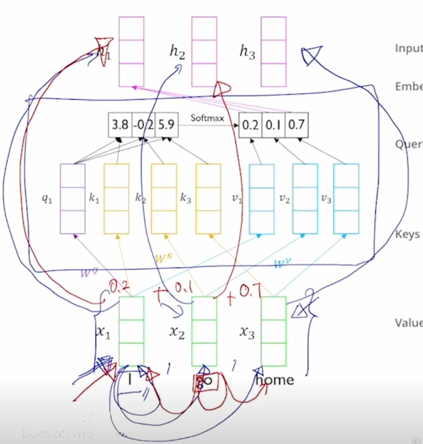
• 그렇게 되면 역시 또 2번째 word 인 “go” 에 대한 입력 vector 를 가지고도 이걸 decoder timestep 의 2번째 hidden state vector 처럼 사용해서 내적을 자기자신과 수행하고 나머지 2개의 vector 들과 내적을 수행하고 거기서 나온 유사도 값을 softmax 를 통해서 새로운 가중치를 얻어서 이 3개의 vector 의 가중평균을 구해서 그걸 “go” 에 대한 encoding vector 로 계산할 수가 있게 됨

• 그래서 기본적으로는 decoder hidden state vector 와 이 vector 를 통해서 유사도를 구하게 되는 encoder hidden state vector 들 간의 구별이 없이 동일한 set 의 vector 들 내에서 이렇게 적용이 될 수 있다는 측면에서 이를 self-attention 모듈이라고 부름

  

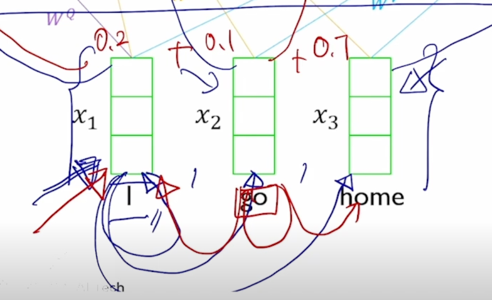
• 이 과정에서 좀 더 자세히 살펴보면

• “I” 라는 vector 가 decoder hidden state vector 로 쓰였을 때 자기 자신과 내적이 될 경우에는 보통 유사도가 서로 다른 vector 와의 내적을 했을 때 보다는 훨씬 더 큰 값으로 도출 됨

  

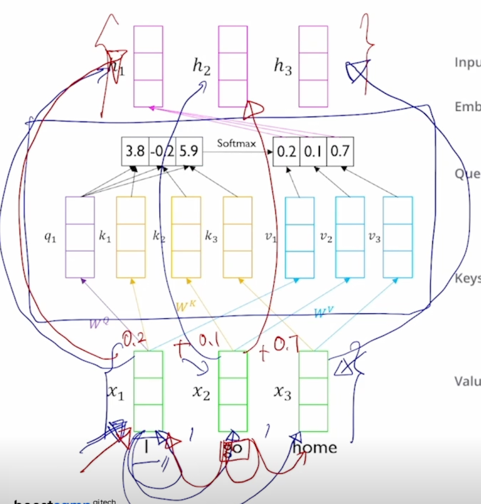
• 그러면 결국 자기자신에게 큰 가중치가 걸리는 그런 형태로 attention vector 의 양상이 나타날 것이고 그렇게 encoding 을 수행한 결과 vector 들도 자기 자신의 원래 정보만을 주로 포함하고 있는 vector 들 만으로밖에 나오지 않을 것임

• 그러면 가장 기본적인 형태의 attention 의 작동과정을 좀 더 유연하게 확장해서 이러한 문제를 개선하는 그러한 형태의 모델로 개선하게 됨

• 그러면 attention 이 수행되는 과정을 좀 더 자세히 보면 주어진 입력 vector 에서의 각 word 에 해당하는 vector 가 그때 그떄 서로 다른 역할을 하고 있는 것을 알 수 있음

• 가령 “I” 라는 word 에 대한 encoding vector 를 얻어내기 위해서는 “I” 가 가지는 입력 vector 가 decoder hidden state vector 인 것처럼해서 우리에게 주어진 vector set 들의 가중치(유사도)를 구하는 그런 형태의 vector 로서 사용이 되었음

  

• 그 경우 주어진 vector 들 중에 어느 vector 를 선별적으로 가져올지에 대한 기준이 되는 vector 로서 역할을 하는데 그 경우를 Query 라고 표현 함

  

• 그 다음엔 Query vector 가 주어진 encoder hidden state vector 의 각 vector 와 내적을 통해서 유사도가 구해지는데 그러면 그 유사도가 구해지는 혹은 계산되는 Query vector 와 내적이 되는 각각의 재료 vector 들을 Key vector 라고 부름

• 결국 Query vector 를 통해서 주어진 여러개의 Key vector 들 중에 어느 해당하는 Key vector 가 높은 유사도를 갖고 있는지 그 유사도 및 어느 것을 가져올지에 대한 정보를 결정해주는 그 역할을 하는 것이 Key vector 에 해당

  

• 마지막으로 그렇게해서 나온 유사도 각각의 Key 와의 유사도를 구한 후 그걸 softmax 를 취한 후 거기서 나온 가중치를 실제로 적용해서 가중평균 혹은 선형결합을 했을 때에 사용하는 재료 vector 들은 앞서 말한 Key vector 와 동일한 vector 로 취급해서 사용하고 있었는데 그렇지만 동일한 vector 였음에도 한번은 유사도를 구하는 Key vector 로 사용됐고 지금은 여기서 구해진 유사도를 바탕으로 그 가중치가 실제 적용되어서 가중평균이 구해지는 재료 vector 로서 사용되는 3번째의 역할을 하는 것으로 생각을 할 수 있음

• 그 3번째 역할을 하는 vector 들을 Value vector 라고 부름

• 그러면 결국 어떤 한 sequence 를 attention 을 통해 encoding 하는 과정에서 Query 로 Key 로 Value 로 이 3가지 역할을 모두 다 하고 있는 것을 볼 수 있음

  

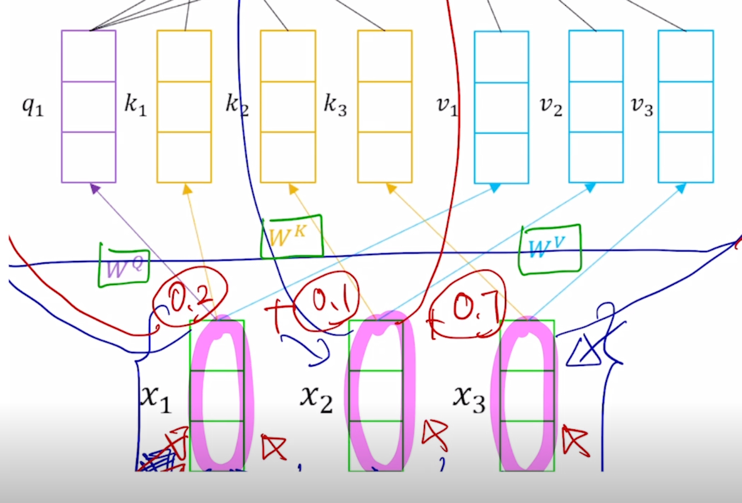
• 이 Transformer 에서 제안된 self-attention 모듈은 동일한 set 의 vector 에서 출발했다고 하더라도 각 역할에 따라 vector 가 서로 다른 형태로 변환할 수 있도록 해주는 별도의 linear transformation matrix 혹은 주어진 vector 가 Query 로 변환될 때의 사용되는 linear transformation matrix $W^Q$ 그리고 주어진 vector 가 Key 로 사용될 때($W^K$) 그리고 Value 로 사용될 때($W^V$)의 적용되는 선형변환 matrix 가 각각 따로 정의되어 있음

• 그렇게 되면 같은 vector 내에서 3가지 역할이 모두 공유가 되는 제한적인 형태가 아니라 주어진 같은 vector 에서라도 Query 로 쓰일 때와 Key 로 쓰일 때와 그리고 Value 로 쓰일 때의 서로 다른 vector 로 변환될 수 있는 확장된 형태가 만들어지게 됨

• 그러면 그렇게 Query, Key, Value 로의 각각의 해당하는 linear translation matrix 를 통해서 변환된 그런 vector 를 생각하고 여기서 다시 attention 모듈을 적용해보도록 하자

  

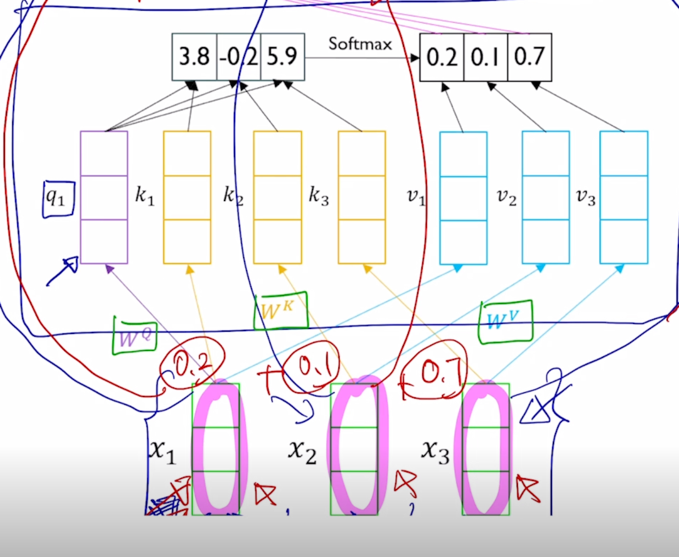
• “I” 라는 word 를 encoding 한다고 생각하면 그 “I” 에 해당하는 입력 vector 가 $W^Q$ 라는 matrix 에 의해서 Query vector($q_1$) 로 변환 됨

• 그리고 이 3개의 vector 들은 Key 그리고 Value vector 들로 변환 됨

  

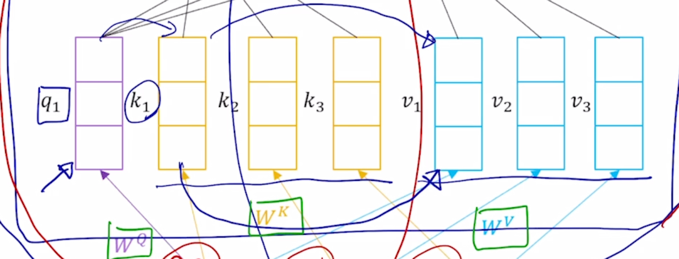
• 그리고 Key 와 Value vector 가 주어졌을 때 한가지 주의할 사실은 첫번째 Key 는 첫번째 Value vector 에 대응하는 즉, 이 Query 가 이 Key 에 적용이되서 유사도 및 softmax 에 의한 가중치가 구해졌을 때 첫번재 Key 에서의 유사도가 적용되는 해당하는 매칭되는 그 Value vector 가 존재

  

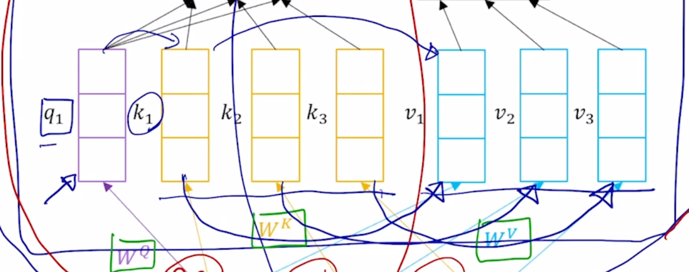
• 2번째 Key vector 에 대해서도 거기서 나오는 유사도가 그래서 나오는 가중치가 적용되는 Value vector 가 또 1대1로 존재한다는 사실을 알 수 있음

• 그래서 Query 는 여기서 하나로 고정되어 있다고 하더라도 Key vector 와 Value vector 는 분리는 되어져 있지만 그 개수는 정확하게 동일해야 한다라는 조건이 만족이 되어야 함

  

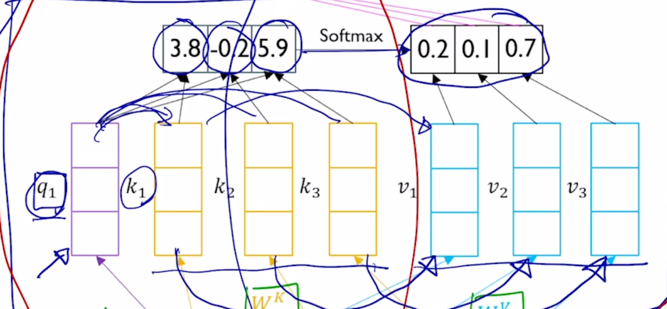
• 이 다음에는 실제로 Query vector 와 각각의 Key vector 를 우리가 알고있는 attention 의 연산과정을 통해서 내적값이 구해지고 그러면 이 내적값을 softmax layer 를 통과를 시켜줌으로써 합이 1인 형태의 확률값을 얻어내게 됨

• 그게 상대적인 가중치가 됨

  

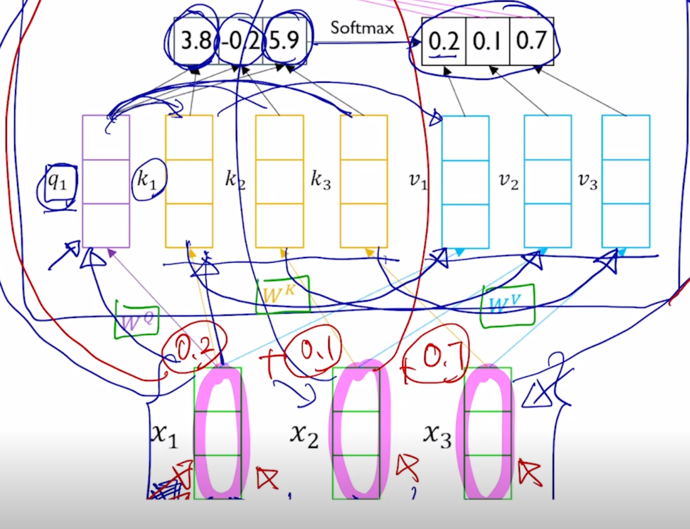
• 그러면 여기서는 보면 첫번째 단어로부터 Query 를 만들었고 첫번째 Key 도 역시 또 첫번째 단어로부터 나온 동일한 단어로부터 만들어진 Query vector 와 Key vector 임에도 불구하고 해당하는 내적값이 다른 Key 와의 내적값보다 더 작을수도 있게 됨

• 이게 Query 와 Key 로의 서로다른 변환이 존재하고 그렇기 때문에 같은 vector 를 가지고 Query 와 Key 를 만들었을 때에도 좀 더 유연한 유사도를 얻어낼 수 있게 됨

  

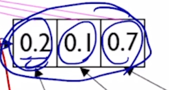
• 그러면 여기서 구해진 20%, 10%, 70% 에 해당하는 가중치는 Value vector 에 부여되는 가중치가 되어서 결국은 Value vector 의 가중평균의 결과로서 최종적인 vector 나오고 그 vector 는 결국 첫번째 word 인 “I” 에 해당하는 word 의 vector 를 Query 로 사용해서 저희에게 주어진 sequence 내에서 필요로하는 가중치를 sequence 내의 다른 단어에 적절히 분배함으로써 각 단어들이 가지는 Value vector 를 가중평균을 해서 결과적으로 얻어낸 vector 라고 할 수 있음

  

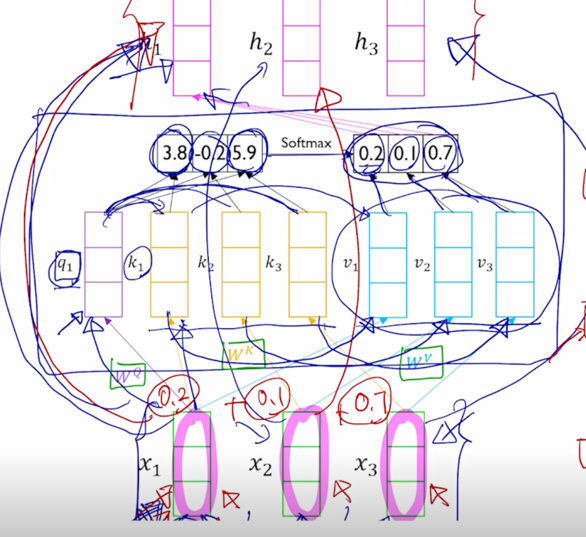
• 이러한 방식으로 “I” 라는 단어에 대한 sequence 전체의 모든 단어들을 적절하게 고려한 형태로의 encoding vector 를 얻어낼 수 있음

• 마찬가지로 두번째 word “go” 에 해당하는 encoding vector 를 얻어낼 때에는 Key 와 Value 는 동일하되 이번에는 Query vector 가 바로 입력 vector $x_2$ 를 $W^Q$ 로 변환한 두번째 단어에 대한 Query vector 가 이번에는 쓰여서 동일한 Key vector 에서의 유사도를 구하고 거기서 나온 새로운 가중치를 바탕으로 Value vector 에 대한 선형결합을 통해서 최종적인 attention output vector 를 얻어낼 수가 있고 그게 결국 “go” 에 해당하는 vector 의 encoding vector 가 됨

  

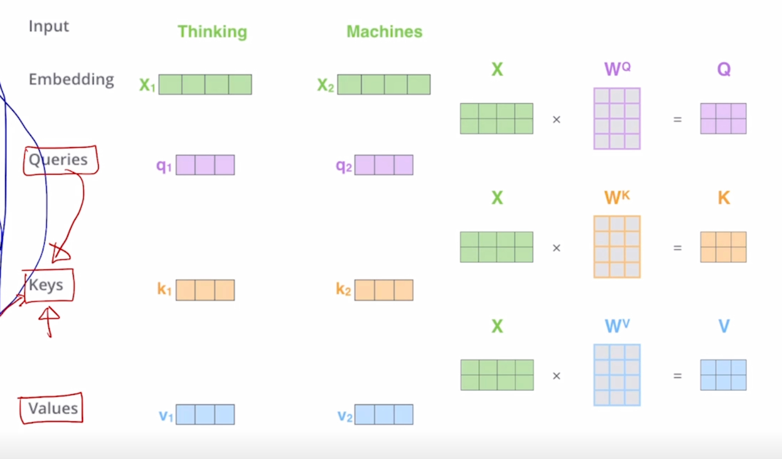
• 여기 보이는 것은 또 다른 예시를 보다 행렬 연산의 관점에서 보여주고 있음

  

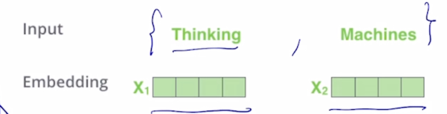
• 입력이 이번에는 2개의 단어로 이루어진 “Thinking”, “Machines” 라는 두 단어로 이루어진 이런 형태에서 각 단어의 입력 vector 가 4차원 vector 이자 이런 row vector 로 나타내어져 있을 때

  

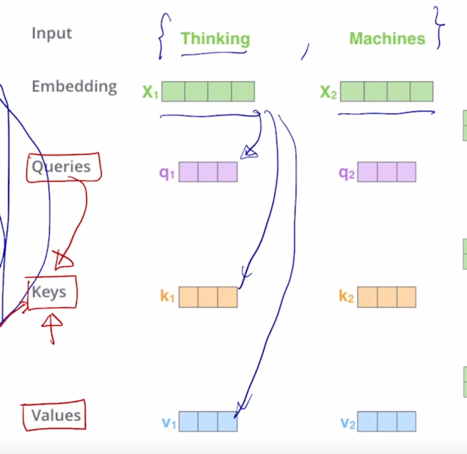
• 각각의 단어들이 Query, Key, Value 로 변환되는 각각의 vector 들을 생각할 수 있음

  

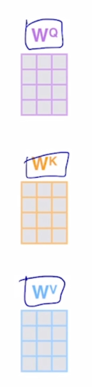
• 그리고 vector 들로 변환되는 과정에서 사용되는 linear transformation matrix 가 $W^Q$, $W^K$, $W^V$ 라고 생각한다면

  

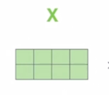
• $X_1$ 과 $X_2$ 이 2개의 vector 를 이러한 방식으로 concat 을 하면

  

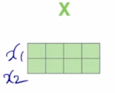
• 첫번째 row 가 $x_1$ 이 되고 두번째 row 가 $x_2$ 가 됨

  

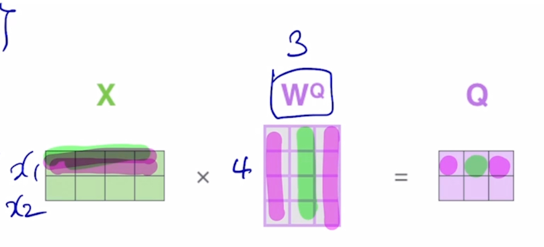
• 그러면 결국 첫번째 word 에 해당하는 4차원 vector 를 $W^Q$ 에 해당하는 vector 와 곱하면 $Q$ 가 나옴

  

• 이 때 $W^Q$ 는 4 x 3 의 사이즈를 가지는 행렬이고 왼쪽에서 입력 word 의 input vector 를 row vector 로 형성해서 matrix 와 곱하게 되면 출력으로 나오는 matrix 의 첫번째 row 는 첫번째 word 에 대한 Query vector 가 됨

  

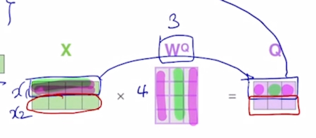
• 마찬가지로 2번째 입력 word 에 대한 embedding vector 가 주어지면 그거를 다시 $W^Q$ 와 곱하면 결과 행렬에서 2번째 row vector 를 형성하게 됨

  

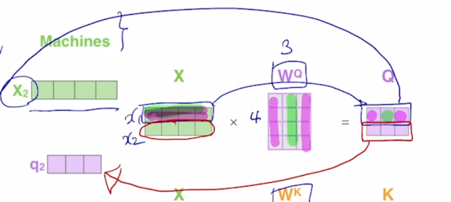
• 그러면 그 row vector 가 바로 두번째 word 에 대한 Query vector 로의 변환결과가 됨

  

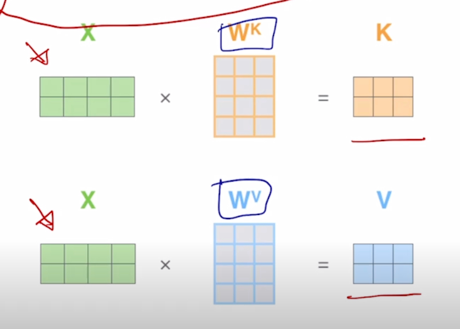
• 마찬가지로 동일한 입력 vector 들을 이렇게 row vector 로 쌓아서 행렬을 구성한 후 그 행렬을 왼쪽에서 $W^K$, $W^V$ 로의 선형변환 matrix 와 곱했을 때 나오는 vector 들이 동일한 set 에서 출발한 vector 들을 서로다른 역할을 하는 Query, Key, Value 로 변환한 그런 결과로 생각할 수 있음

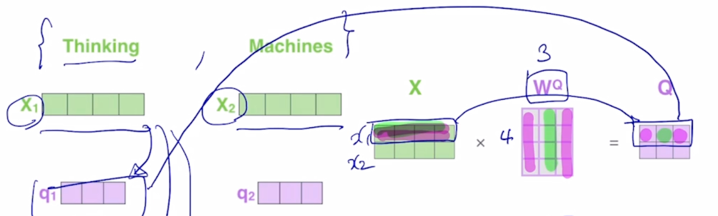
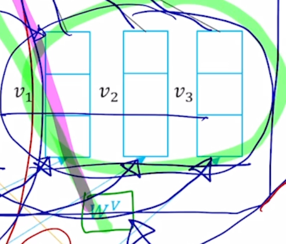
• 그러면 앞서 RNN 의 구조에서 정보의 흐름의 측면에서 말했던 것처럼 여기서도 각각의 단어들에 대한 encoding vector 를 구할 때 정보가 어떤 방식으로 반영이 되는지에 대한 패턴을 생각해보자.

  

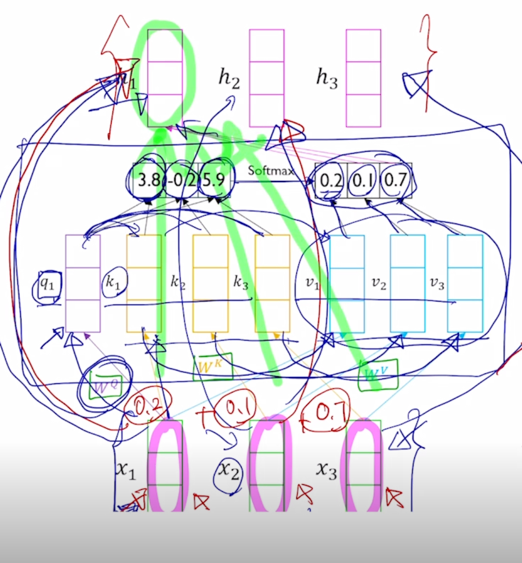
• 첫번째 word 에 대한 encoding vector 는 초록색 부분인데 내부적인 attention 과정에서 봤던것처럼 3개의 단어가 모두다 참여하는 것을 알 수 있음

• Value vector 로의 변환 그리고 이 Value vector 에 대한 가중평균으로서 encoding vector 가 계산이 됨

  

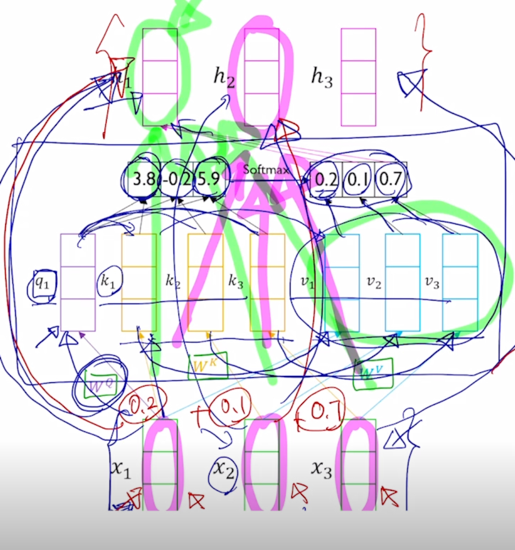
• 마찬가지로 2번째 word 의 encoding vector 의 결과값도 모든 단어로부터의 정보를 고려해서 적절하게 잘 정보를 결합하는 vector 를 만들어내는 것을 알 수 있음

• 여기서 중요한건! sequence 길이가 굉장히 길다고 하더라도 self-attention 모듈을 적용해서 sequence 내 각각의 word 들을 encoding vector 로 만들게되면 그 tiemstep 의 gap 이나 그 차이가 굉장히 멀었음에도 불구하고 이 경우에도 이들이 다 동일한 Key 와 Value vector 들로 변환이 되고 Query vector 에 의한 내적에 의한 유사도만 높다면 timestep 의 차이가 멀다고 하더라도 멀리있었던 정보를 손쉽게 가져올 수 있음

  

• 이것이 기존의 RNN 에서 보이던 한계점 즉, 분홍색의 위치의 정보를 encoding 하기 위해서 멀리서의 정보를 가져오려고 하면 RNN 모듈을 timestep 의 차이만큼 연속적으로 혹은 반복적으로 통과해줘야 한다는 그래서 정보의 손실이나 변질이 많이 일어날 수 있는 이런 한계점을 근본적으로 개선한 형태의 모듈로 볼 수 있음

• 그래서 결론적으로 self-attention 모듈은 Long-Term Dependency 의 문제를 근본적으로 깔끔하게 해결을 한 그런 형태의 sequence encoding 기법으로 생각할 수 있음

Trnasformer: Scaled Dot-Product Attention

• attention module 의 수식적인 과정을 살펴보자.

• Inputs: a query $q$ and a set of key-value ($k$, $v$) pairs to an output
  • attention module 의 입력은 하나의 query vector 인 $q$ 가 있을 것이고 그 다음은 key 와 value vector 의 쌍으로 이루어진 다수의 key-value pair 들이 존재 함
• Query, Key, Value, and output is all vectors
• Output is weighted sum of values
  • 그러면 기본적으로 Query vector 를 encoding 을 한 output vector 는 결국 Value vector 에 대한 가중평균이 됨
• Weight of each value is computed by an inner product of query and corresponding key
  • 그 가중평균에서 쓰이는 가중치는 Query vector 와 그리고 Value vector 에 해당하는 Key vector 와의 내적값을 통해서 구해짐
• Queries and keys have same dimensionality $d_k$, and dimensionality of value is $d_v$
  • Query vector 와 Key vector 는 기본적으로 내적연산이 가능해야 되기 때문에 같은 dimension 혹은 같은 차원의 vector 여야 함
  • 그래서 그 vector 의 차원을 $d_k$ 라고 하고 Value vector 의 경우는 Query 나 Key vector 와의 차원과는 꼭 같지 않아도 됨

  • 여기서 보시면

    

    

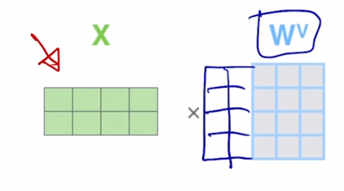
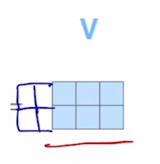
  • $W^V$ 를 통한 변환이 가령 $W^V$ 의 사이즈가 2줄이 더 있다라고 하면 그러면 Value vector 의 최종적인 차원도 5차원 vector 가 됨

    

  • 그러면 여기에 주어지는 Value vector 가 5차원이 되면 결국 5차원 vector 3개의 대해서 상수배를 해서 가중평균을 내는 것이기 때문에 애초에 Query 와 Key vector 의 차원과는 꼭 같지 않아도 attention 모듈이 실행되는데는 아무 문제가 없음
  • 그래서 일반화된 표현으로서 Value vector 의 dimension 은 $d_v$ 라고 생각할 수 있음

\[A(q, K, V) = \sum_{i} \frac{exp(q \cdot k_i)}{\sum_{j} exp(q \cdot k_j)} v_i\]

• Attention 모듈의 입력은 Query vector 하나, 그리고 Key 와 Value vector 들의 pair 들의 집합이 됨

• 그러면 여기서 K, V 라고 대문자로 나타낸 것은 앞서 보여드린 예시처럼 대문자로 쓰여진 것이 하나의 행렬을 나타낼 때 그 행렬의 각각의 row vector 가 가령 Query vector 혹은 Key vector 혹은 Value vector 인 이런 형태로 되서 각각의 vector 들을 row 형태로 쭉 합쳐놓은 하나의 행렬을 의미

  

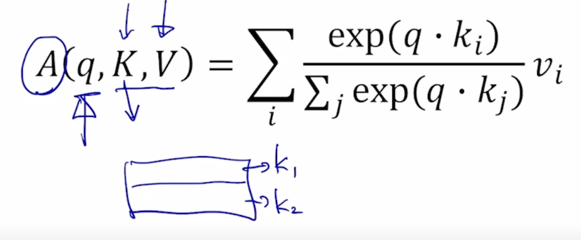
• 그러면 이 $K$ 가 “Thinking”, “Machines” 같은 경우 2줄의 row vector 가 있음

  

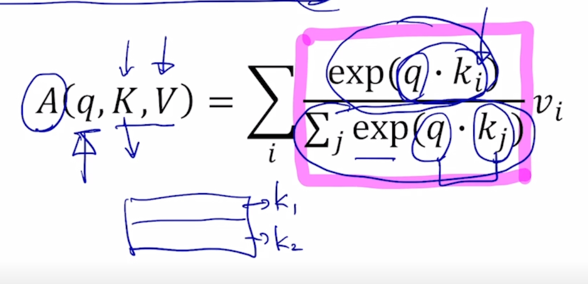
• Query vector 와 Key vector 각각과의 내적을 구한 후 그걸 모두 exponential layer 를 통과한 후 그걸 다 더하고 그 다음에 i 번째 Key 에 해당하는 유사도에서 가지는 exponential 을 취한 값 그 상대적인 비율을 구하면 i 번째 Key 로 부터 구해진 softmax 를 통과하고 나서의 유사도 값이 됨

  

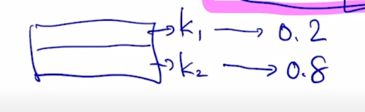
• key 가 1일 때는 유사도 값이 0.2 그리고 두번째 key 에서의 유사도는 0.8 이렇게 나올 수 있음

  

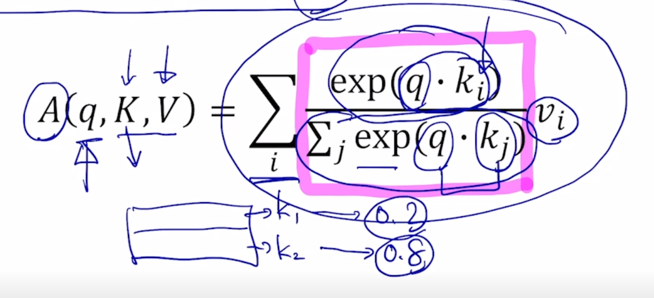
• 그 다음에 0.2 와 0.8 이라는 값에 그에 해당하는 매칭되는 Value vector 를 곱해서 그걸 다 더해주고 나면 이게 value vector 에 대한 가중평균 으로서 최종 결과가 나오게 됨

• 그러면 당연히 Query 를 attention 모듈을 통해서 encoding 한 vector 는 최종적인 차원으로는 $d_v$ 차원 만큼의 vector 가 나옴

• 그러면 앞서 이해했던 attention 모듈의 입력과 출력간의 관계를 좀 더 확장한 형태로 생각해보자.

• When we have multiple queries $q$, we can stack them in a matrix $Q$:

  \[A(q, K, V) = \sum_{i} \frac{exp(q \cdot k_i)}{\sum_{j} exp(q \cdot k_j)} v_i\]

• Becomes:

  \(A(Q, K, V) = softmax(QK^T)V\)

  • 여기서 확장은 Query vector 가 단일한 하나의 vector 가 아니라 Query vector 자체도 다수의 Queyr 가 주어지는 어떤 입력을 받은 attention 모듈이 확장된 형태가 됨
  • 앞서 말한것과 비슷하게 $Q$ 라고 하는 Query vector 를 각각의 row 로 가지고 있는 matrix 가 주어져 있다고 생각을 하자

  

  • 그러면 이 행렬의 크기는 $\mid Q \mid$ 로 나타내면 Query 의 개수와 각각의 Query 이 차원이 열의 개수가 될 것임

  

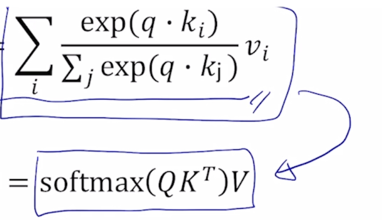
• 그다음은 이 식을 이해해보고자 함

  

• Q 는 ($\mid Q \mid \times d_k$) 가 되고

  

• Key matrix 는 원래는 key vector 들이 row 형태로 담겨져 있는 형태였을 건데 transpose 라는 연산을 통해서 행렬이 대각선으로 대칭된 형태로서 주어져서 $K^T$ ($d_k \times \mid K \mid$)가 주어지는 형태가 됨

  

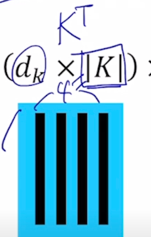
• $K^T$ 의 사이즈를 볼 때 기본적으로 Key 가 4개가 있는 상황이고 이게 key 의 개수이고 $d_k$ 는 key vector 가 가지는 vector 의 dimension 이 됨

  

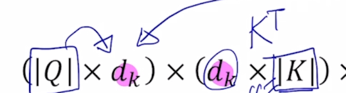
• 당연히 key vector 의 dimension 과 query vector dimension 은 같아야 함

• 그 다음엔 $Q$ 와 $K^T$ 라는 matrix 연산을 한번 생각해보자

  

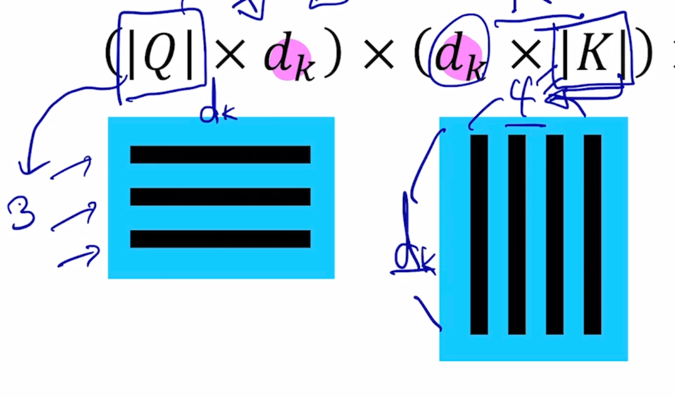
• 두 행렬이 곱해지면 (3 x $d_k$) ($d_k$ x 4) query 가 3개고 key 는 4개인 상황

  

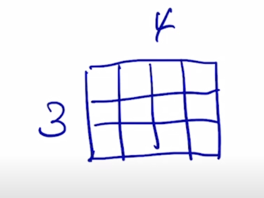
• 여기서 나타나는 행렬곱의 결과 matrix 는 3 x 4 의 행렬로 나타남을 알 수 있음

• 여기서 각각의 element 가 어떤식으로 계산되는지 보자

  

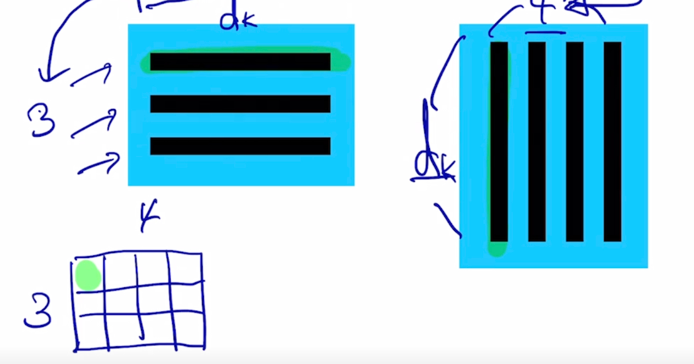
• 첫번째 query vector 에 대해서 각각의 key vector 와 내적을 수행해 보면 이 값이 나오게 되고

  

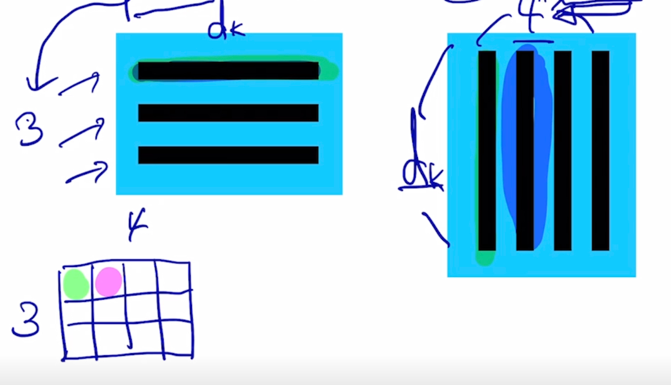
• 그리고 또 동일한 query vector 에 대해서 이번엔 두번째 key vector 를 또 내적을 하게 되면 두번째 vector 가 나올 것이고

  

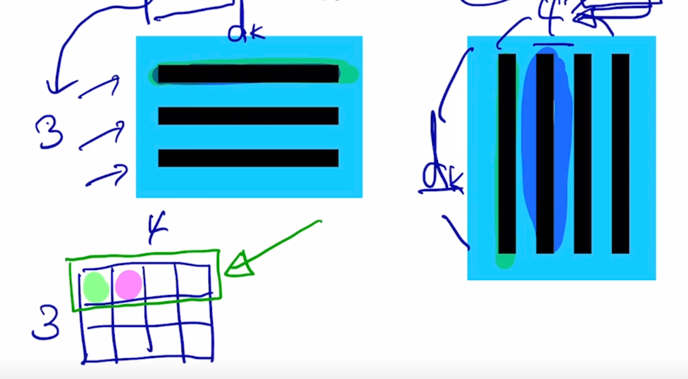
• 그러면 마찬가지로 내적값을 각각의 key vector 들과 수행한 후에는 첫번째 query 에 대한 내적에 기반한 key vector 들과의 유사도는 결과 matrix 의 첫번째 row 에 형성되는 것을 알 수 있음

  

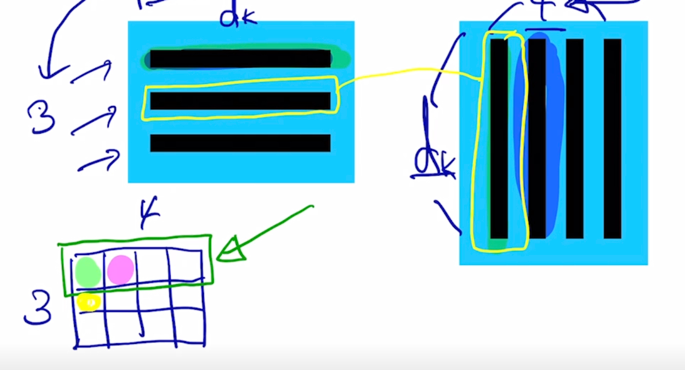
• 마찬가지로 2번째 query 를 사용한 경우에는 2번째 query 와 첫번째 key 를 내적을 해서 나오는 scalar 값은 바로 노란색점이 될 것이고

  

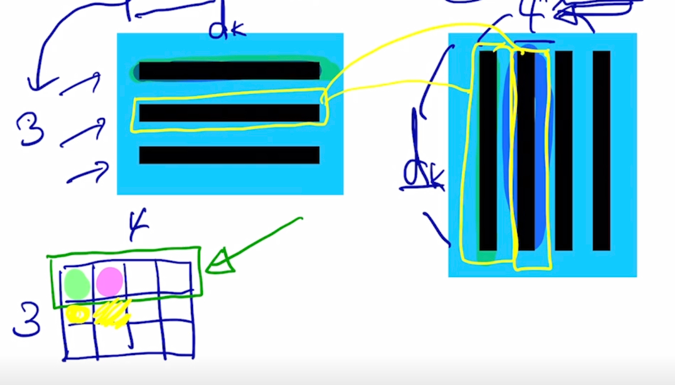
• 마찬가지로 2번째 key 와 내적을 수행하게된 그때의 scalar 내적값은 바로 옆자리가 될 것임

  

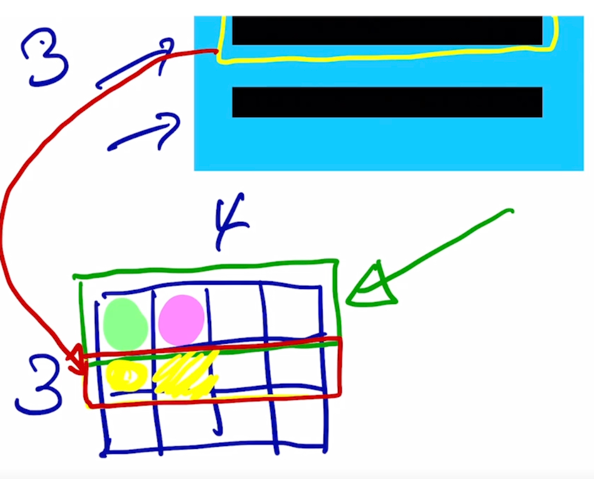
• 결국 그러면 마찬가지로 결과 matrix 에서 2번째 row 는 2번째 query 가 각각의 key vector 와 내적이 되어서 나오는 유사도 값을 담고 있는 것으로 생각할 수 있음

  

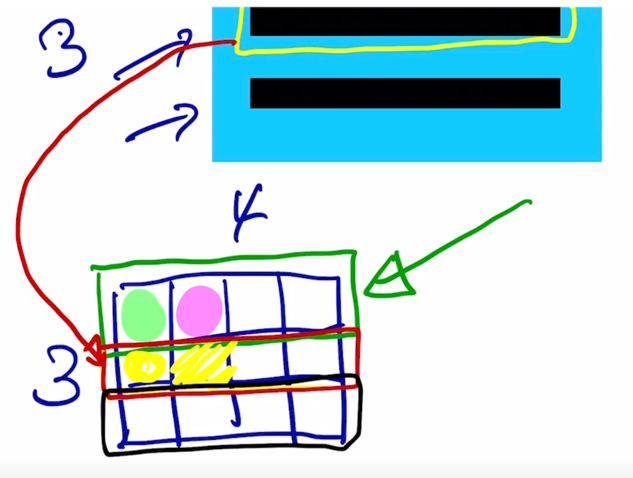
• 그리고 마찬가지로 3번째 row 도 3번째 query 에 대한 내적에 기반한 유사도를 담고 있게 됨

  

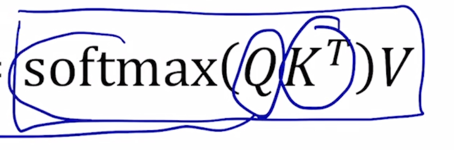
• 여기에 다음으로 적용해 줄 연산은 바로 softmax 연산임

  

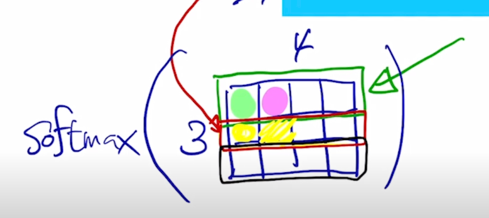
• 이 softmax 를 이 행렬에 걸어주게 됨
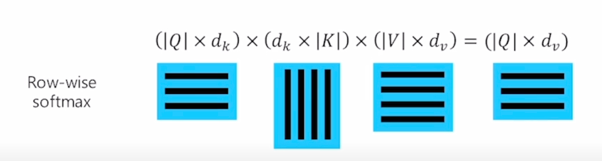
• softmax 는 행렬이 주어졌을 때에는 default 로 Row-wise softmax 를 생각함
• 결국 행렬이 주어지면 각각의 row vector 들에 대해서 softmax 연산 혹은 변환을 수행함

• 자 그러면 softmax 를 각각의 row 별로 수행한 다음의 결과 matrix 는 첫번째 query 에 대한 4개의 key 에 대한 합이 1인 형태의 가중치가 나오게 됨

  

• softmax 까지 계산했을 때 나오는 행렬값이 이런 식으로 첫번째 query 에 대한 합이 1인 형태의 가중치가 나오게 될 것임

• 두번째, 세번째 row 도 마찬가지임

  

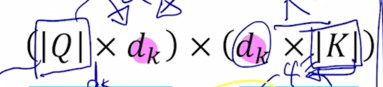
• 이게 여기까지의 결과임

  

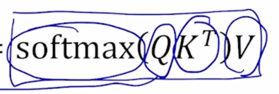
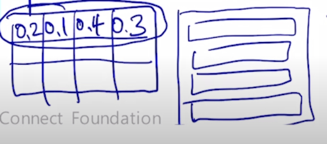
• 또 Value matrix 를 옆에 또 곱해주게 되면 이 경우에 또 어떻게 계산이 되는지 살펴보자

  

• Key 개수도 4개고 Value 개수도 4개가 됨

  

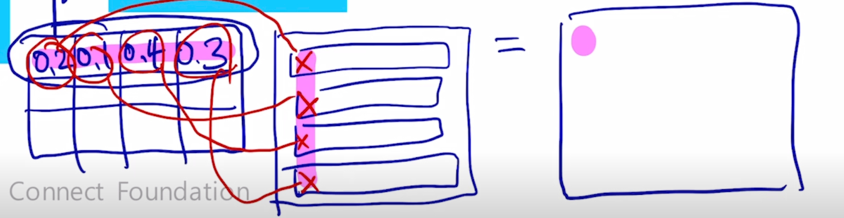
• 여기서 계산되는 행렬을 계산해보면 첫번째 query 에 대해서 나온 attention 가중치 혹은 attention vector 의 값과 Value vector 의 첫번째 column 과 곱해서 첫번째 element 를 만들게 됨

• 마찬가지로 동일한 가중치 vector 를 Value vector 의 2번째 row 에 적용해보자.

  

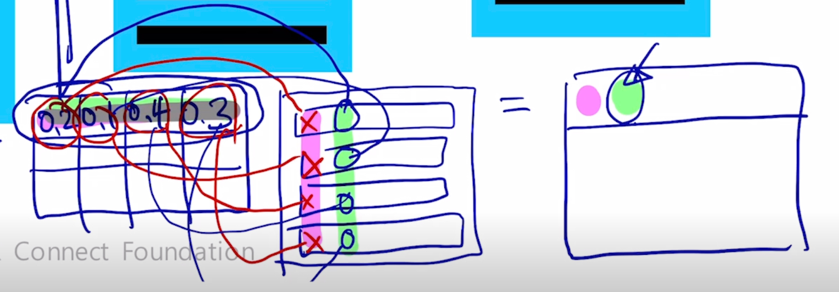
• 그렇게해서 만들어진 내적값은 결과 matrix 에 첫번째 row 에 2번째 element 를 구성하게 됨

  

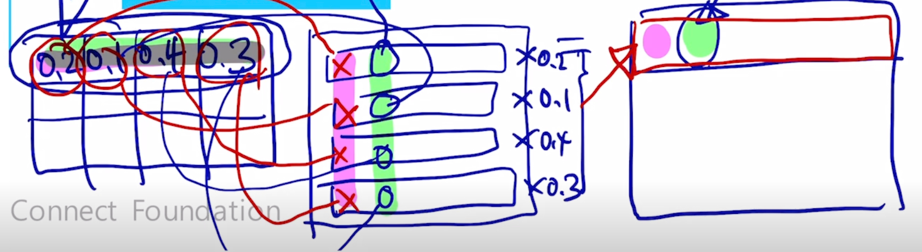
• 결국 이를 확장해보면 첫번째 row vector 에 0.2, 두번째 row vector 에 0.1, 세번째 row vector 에 0.4, 네번째에 0.3 이러한 row vector 별로 각각 가중치를 다 곱한 후 이를 다 더해서 만들어지는 vector 가 여기 결과 matrix 의 첫번재 row vector 를 형성한다는 것을 알 수 있음

  

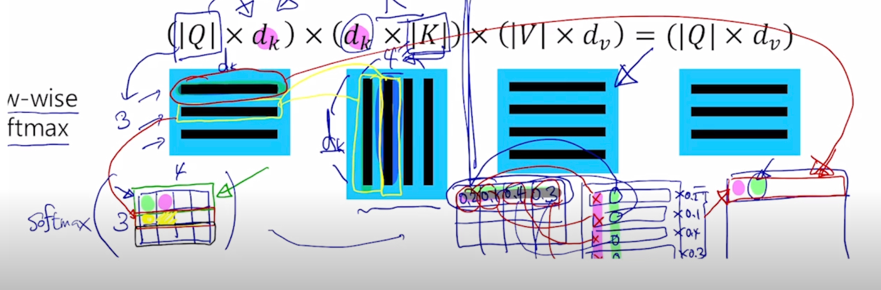
• 그러면 결국 결과 matrix 의 첫번째 row vector 는 맨처음에 주어졌던 Query matrix 의 첫번째 row vector 이자 첫번째 query vector 에 대한 attention 모듈의 output vector 를 의미하게 됨

  

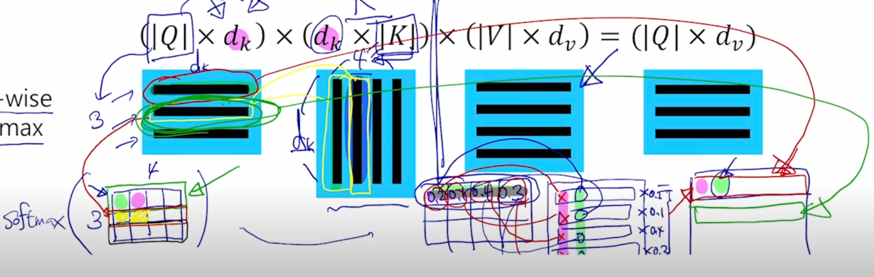
• 마찬가지로 여기서 생성되는 결과 matrix 의 2번째 row vector 는 2번째 query vector 를 사용해서 만들어진 attention 모듈의 output vector 로 계산되게 됨

• 이러한 행렬곱을 통해서 Key - Value 가 다수의 pair 로 주어졌을 때 뿐만 아니라 Query vector 도 여러개가 주어져서 각각의 Query 에 대한 attention 모듈의 output 을 계산해야하는 이런 상황을 Query 를 한데모아서 row vector 로서 행렬을 구성한 후 결국 이러한 $ softmax(QK^T)V $ 수식으로 이루어진 행렬연산을 수행하면 결국 모든 각각의 Qeury vector 에 대한 attention 모듈의 output vector 를 한번에 계산할 수 있음
• 이렇게 여러 query vector 에 대한 attention 모듈의 계산을 행렬연산으로 바꿔두면 행렬연산을 빠르게 병렬화해서 계산할 수 있는 GPU 를 활용해서 이러한 계산을 효율적이고 빠르게 수행할 수 있음

• 이러한 병렬적인 행렬연산이 가능하다는 특성을 통해서 이전의 RNN 모델등의 비해서 상대적으로 학습이 굉장히 빠른 그런 특성을 가지게 됨

• 실제 Transformer 구현 상으론 동일한 shape 로 mapping 된 Q, K, V 가 사용되어 각 matrix 의 shape 는 모두 동일

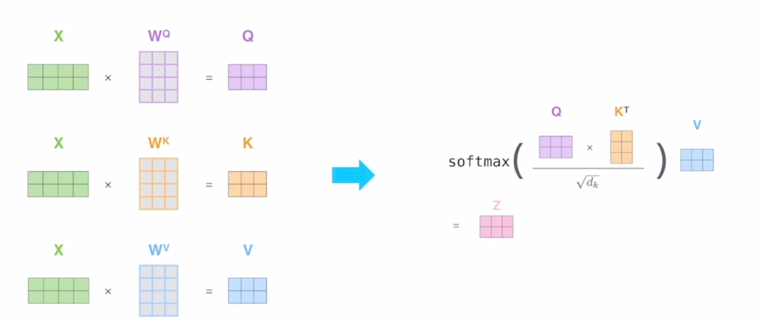
• 앞서 나왔던 “Thinking”, “Machines” 라는 2개의 단어로 이루어진 sequence 를 encoding 하는 과정을 도식화된 그림으로 다시 살펴보자.

• Example from illustrated transformer

  

  

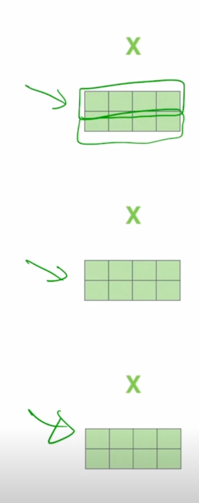
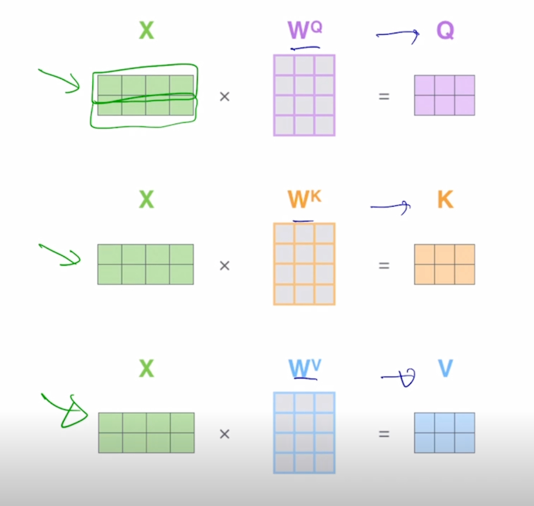
• 동일한 입력벡터가 각각의 word 가 row vector 인 형태로 행렬을 구성해서 입력 matrix 를 형성했을 경우에

  

• 동일한 matrix 가 $W^Q$, $W^K$, $W^V$ 로 변환되면서 각각의 Query, Key, Value matrix 로 변환이 됨

  

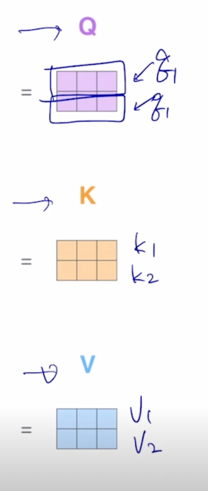
• 여기서는 구체적으로 각 matrix 에서의 row vector 가 입력 sequence 에서 주어진 2개의 word 각각에 대한 Query vector 가 되고, Key vector 가 되고 Value vector 가 된다는 것을 알 수 있음

  

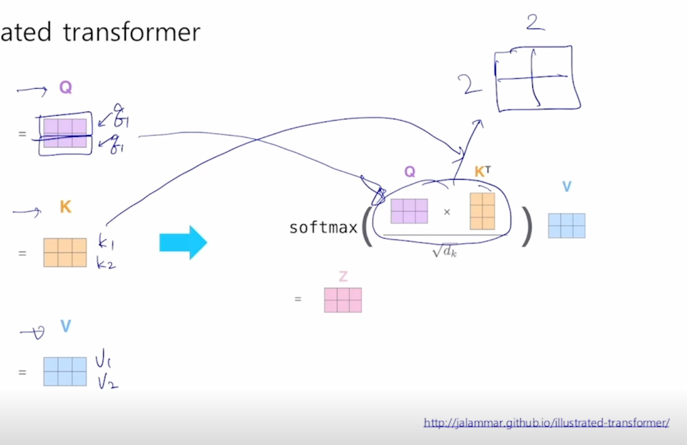
• attention 모듈의 output 을 계산해보면 Query 로 변환된 행렬을 가져오고 Key 행령를 Transpose 를 해서 계산하면 이 부분은 결국 2 x 2 짜리의 행려이 나옴

  

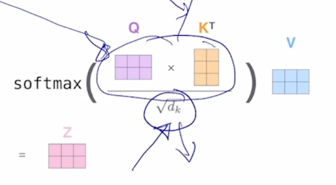
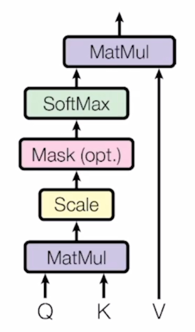
• 여기서 Square root $\sqrt{d_k}$ 로 나눠주는데 이 부분은 attention 을 수행할 때 Query, Key 에 대한 내적연산을 수행함으로써 attention 을 계산하는데 상수로서 나타나는 $d_k$ 의 root 로 행렬의 모든 원소들을 나눠준 후 softmax 를 적용하게 됨

  

• Scaled 에 해당하는 이 부분은 밑에서 설명하기로 하고 지금은 무시하도록 함

  

• 그러면 이게 첫번째 Query vector 와 두번째 Query vector 가 각각의 Key vector 와의 내적을 통한 유사도가 되고

  

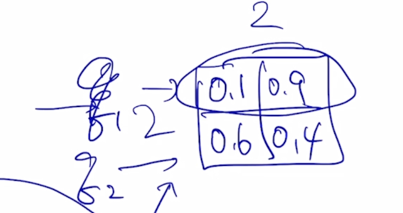
• 거기에 row-wise softmax 를 계산하면 결국은 각각의 row 들이 합이 1인 형태로 바뀌게 됨

  

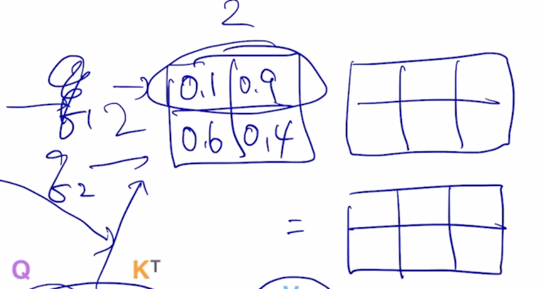
• 그러면 이 vector 에 Value vector 가 row vector 로 나타내어지는 행렬을 오른쪽에서 곱하게 되면 동일한 2 x 3 matrix 가 나타나고

  

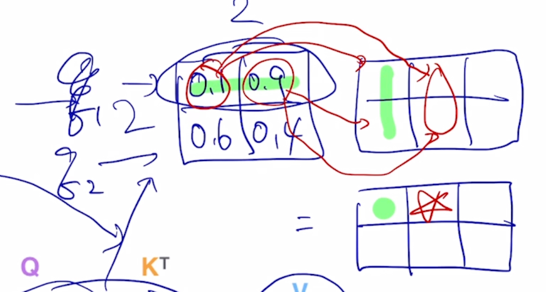
• 내적을 수행해보면 초록색 라인을 따라서 내적을 통해 값을 만들어내게 되고 별을 만들어내는 형태가 됨

  

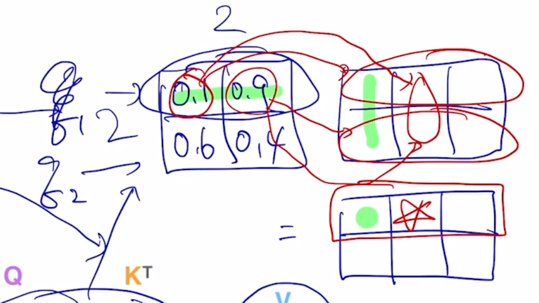
• 마찬가지로 여기 있는 2개의 row vector 에 가중치를 0.1 과 0.9를 적용해서 만든 가중평균 vector 가 여기에 추가 되는 것을 알 수 있음

• 두번째 Query 에 대한 attention vector 를 사용해서도 새로운 가중평균된 vector 즉, Value vector 의 가중평균 vector 가 나오게 됨

• 다음으로는 앞서 말한 Query 와 Key 내적을 계산할 때 추가적으로 붙는 Scaling 과정인 $\sqrt{d_k}$ 로 내적값을 나누어주는 이 부분이 어떤 역할을 하는지 설명해보자.

• Problem
  • As $d_k$ gets large, the variance of $q^Tk$ increase
  • Some values inside the softmax get large
  • The softmax gets very peaked
  • Hence, its gradient gets smaller
• Solution
  • Scaled by the length of query / key vectors:
  \[A(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]

  

• 기본적으로 $QK^T% 에서 나오는 각각의 element 들은 특정 Query vector 하나와 Key vector 내적의 형태로 계산됨

• Query 와 Key vector 가 가지는 공통된 dimension 수가 2차원이라면 내적 값은 언제나 내적값이 scalar 로 나오긴 하지만 scalar 값을 계산하는데 참여하는 Query 와 Key vector 의 차원수는 가령 2차원일수도 있고 100차원의 vector 일 수도있고 다양한 차원수가 정의될 수 있음

  

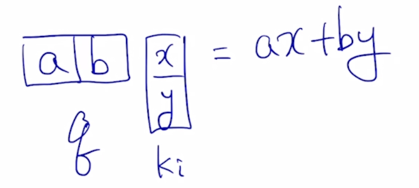
• 그러면 현실적으로 2차원 vector 의 Query 와 Key vector 를 생각하면 위의 형태로 나타내어질 수 있음

  

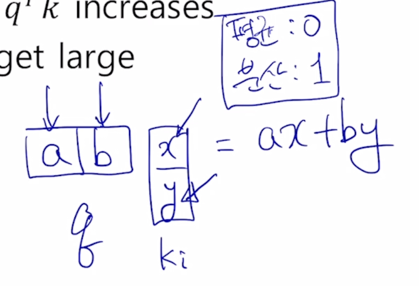
• 통계적으로 혹은 평균적으로 볼 때, Query vector 와 Key vector 의 각각의 원소의 값이 특정한 평균과 분산을 가지는 확률변수로 생각해보자.

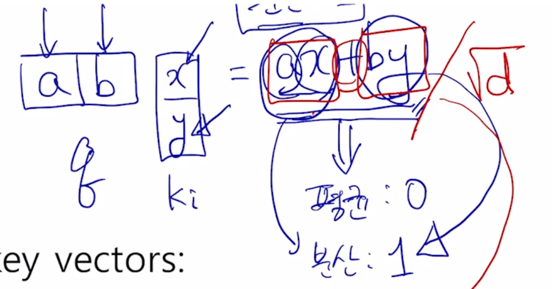
• a, b, x, y 가 각각 통계적으로 독립인 평균이 0이고 분산이 1인 형태로 생각해보자.

  

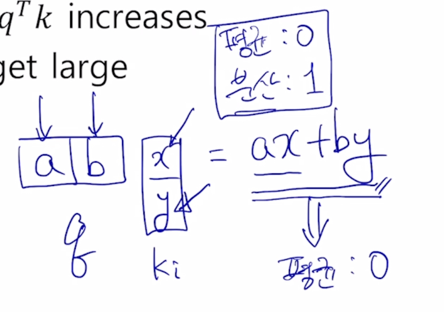
• 2차원에서 적용되는 vector 의 내적의 평균과 분산이 어떻게 되는가를 보면 ax, by 각각의 평균이 모두 0이기 때문에 내적값의 평균도 역시 0이 됨

  

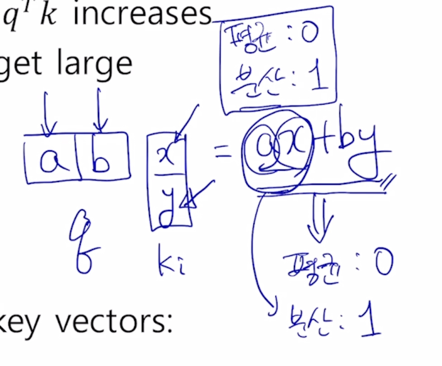
• 다음은 분산이 중요한데 a 와 x 가 각각 통계적으로 독립인 분산이 1인 그런 random variable 이 곱해지면 ax 에 대한 분산은 역시 1이 나오게 됨

• 이에 대한 자세한 증명은 생략하기로 하고 확률통계쪽에 관련 교재나 과목에 증명이 나타나 있음

  

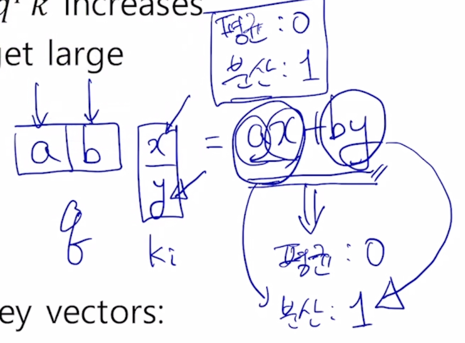
• by 도 역시 둘이 통계적으로 독립인 random variable 이 곱해졌을 때 나오는 분산이 또 1이됨

• 두 부분이 각각 분산이 1인 형태의 random variable 이라고 하면 이 2개가 결국 더해지는 형태의 새로운 random variable 은 각각의 random variable 의 분산의 합과 동일하다는 것이 알려져 있음

  

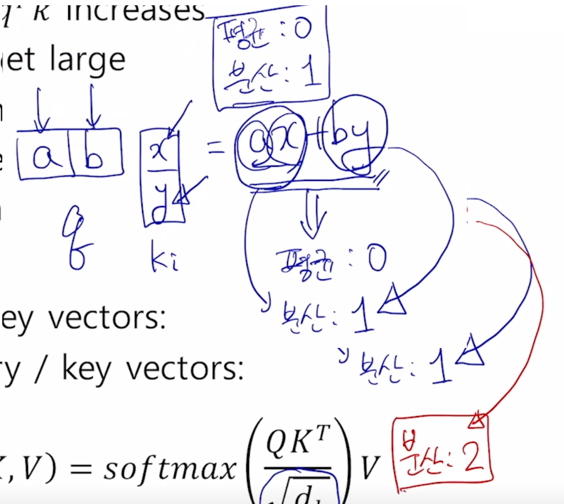
• 이 경우 최종적인 분산은 2가 되는 형태가 됨

  

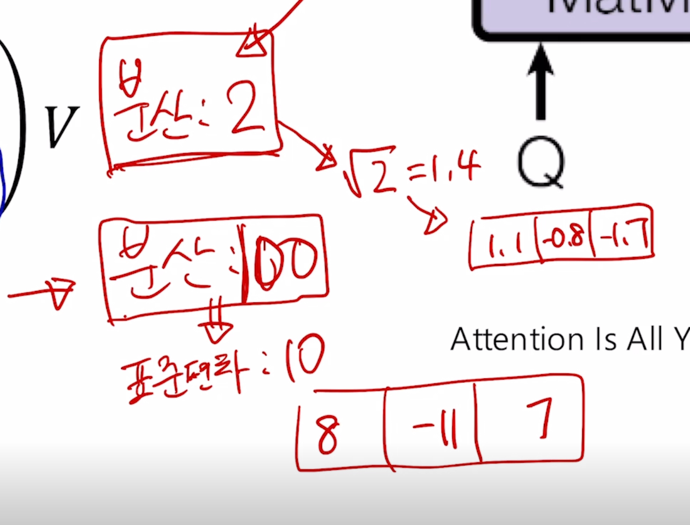
• 가령 Query 와 Key vector 의 차원이 100 차원으로 구성된 vector 의 내적을 수행했을 때를 생각해보자.
• 100차원 vector 둘 그리고 각각의 vector 의 원소가 통계적으로 독립이고 평균과 분산이 0, 1 인 경우를 가정하면
• 그 때는 분산이 내적에 참여하는 dimension 이 이번엔 2차원이 아니라 100차원이 되기 때문에 이 경우 분산이 100이 됨

• 가령 Qeury vector 하나에 대해서 Key vector 가 총 3개로 주어진 경우에는 dimension 이 10 인 Query 와 Key vector 에 대해서 내적으로 계산되는 유사도가 기본적으로 표준편차를 생각해볼 수 있고 이 때 표준편차는 10 정도가 되니까 그 때 나오는 값이 평균은 0이어야 하고 이 때 나오는 내적값의 기반한 유사도는 가령 8 그리고 -11 그리고 7 이정도의 3개의 Key 에 대한 내적값이 이렇게 나타날 수 있고 가령 분산이 2인 경우는 표춘편차가 $/sqrt{2}$ 밖에 안되기 때문에 이 경우 Key vector 가 3개가 있을 경우 내적에 기반한 특정 Query 에 대한 유사도는 가령 1.1, -0.8, -1.7 이런식으로 표준편차가 대략 1.4 정도가 되는 그런 값들로 분포가 나오게 됨

  

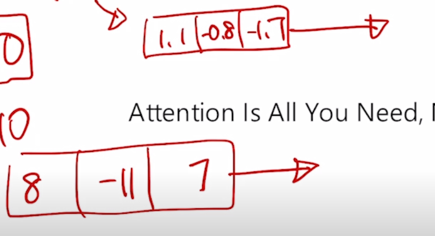
• 그러면 이때, 100 dimension 으로의 내적값으로 나온 유사도를 softmax 의 입력으로 주고 2 dimension 에서의 내적으로부터 나온 유사도를 softmax 로 주게되면 기본적으로 분산 혹은 표준편차가 클수록 softmax 의 확률분포가 큰 값에 몰리는 패턴이 나나탐을 알 수 있음

• 거꾸로 분산이 작은 경우에는 확률분포가 좀 더 고르게 각 3개의 Key 들에 대한 확률값이 평균적으로 30 ~ 50% 사이의 Uniform distribution 의 형태로 나타나게 됨

  

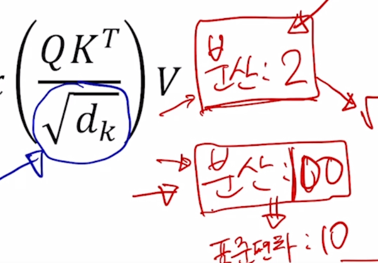
• 그래서 내적에 참여하는 Query 와 Key vector 의 dimension 이 몇이냐에 따라 내적값의 분산이 크게 좌지우지 될 수 있고 또 이에따라 softmax 로 부터 나오는 확률분포가 굉장히 어떤 한 Key 에만 100% 에 가까운 확률이 몰리는 극단적인 형태의 확률이 나올지 혹은 전반적으로 모든 Key 가 고른 확률값을 부여받은 형태로 나올지 이런 softmax 의 확률분포의 패턴이 의도치않게 Query 와 Key 의 dimension 때문에 영향을 받게 됨

  

• 그래서 이 내적값에 분산을 일정하게 유지시켜 줌으로써 학습을 안정화 시켜주기 위해서 이렇게 나온 내적값에 $\sqrt{d_k}$ 값으로 나눠주는 연산을 추가적으로 넣게 됨

• 여기 d 는 2가 될 것이고

  

• 100 dimension 에서 나온 내적값은 $\sqrt{100}$ 혹은 10으로 내적값을 나눠주게 되면

• 특정한 상수로 주어진 Random variable 을 나눠줬을때는 그때는 분산 혹은 표준편차가 분산인 경우는 이 값의 제곱으로 나눠지는 것을 알 수 있고 그래서 결국은 분산의 측면에서는

  

• $\sqrt{2}$ 의 제곱인 2 그리고 $\sqrt{100}$ 의 제곱인 100으로 분산이 줄어들기 때문에 결국은 최종적으로 $QK^T$ 의 각 element 가 실제로 Query, Key 의 dimension 이 몇이었든지간에 샹관없이 분산이 일정하게 1인 형태로 유지되는 그런 값이 나오게

  

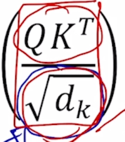
• 그래서 softmax 의 output 에서의 확률분포였던 한쪽으로 몰리는 정도가 의도치 않게 dimension 에 영향을 받지않도록 scaling 을 추가적으로 attention 모듈에 내적기반 유사도를 구할때에 추가를 해주게 됨

• 결과적으로는 softmax 의 값이 한쪽으로 굉장히 몰리게 되는 경우에는 실질적으로는 그러한 상황에서 학습을 진행할 때 gradient 혹은 backpropagation 이 gradient vanishing 이 잘 발생될 수 있는 위험성이 있음
• 의도치 않게 차원을 크게 설정하고 scaling 없이 attention 모듈을 수행했을 때 종종 학습이 전혀 되지 않는 그런 상황이 벌어지는 경우가 종종 있는데 그런 경우에서처럼 softmax 의 output 을 적절한 정도의 범위로 조절하는 것이 학습에도 실제로 중요한 역할을 하게 됨