Day_81 02. 찾은 모델 잘게 찢기: Tensor Decomposition 실습

찾은 모델 잘게 찢기: Tensor Decomposition 실습

1. 이론 요약

1.1 Tensor notation, operation

Vector Outer Products

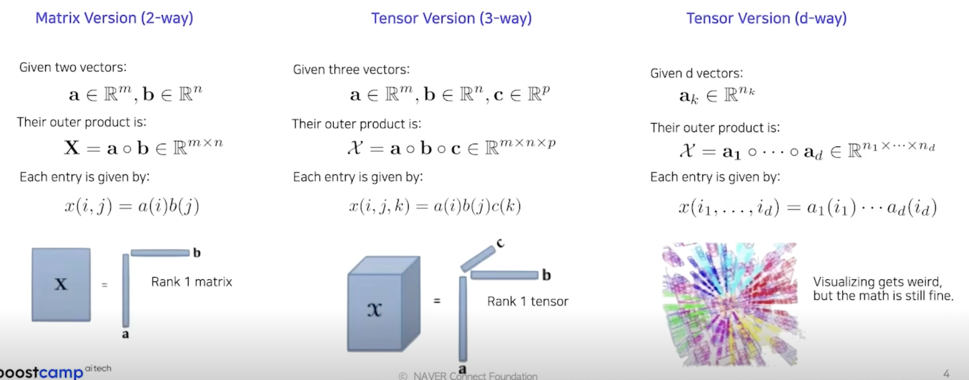
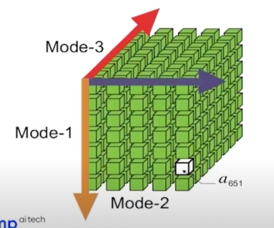
Tensor: multidimensional array

• Mode denotes each dimension
  • axis 라고 봐도 되고 dimension 이라고 봐도 됨
• Fiber: A vector obtained by fixing all but one of tensor’s indices
  • 결국은 vector
• Slice: A matrix obtained by fixing all but two of tensor’s indices
  • 일종의 matrix

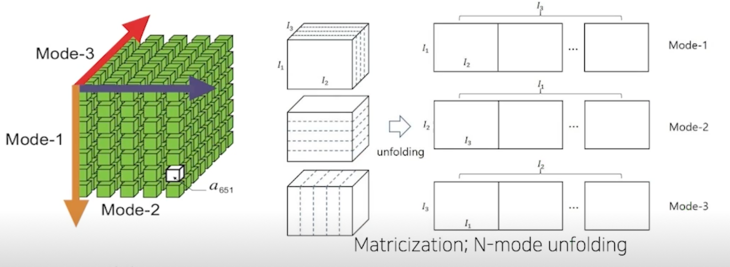
Tensor unfoldings: matricization and vectorization

• Matricization: convert a tensor to a matrix
• Vectorization: convert a tensor to vector
• N-mode unfolding: n-mode dim 을 기준으로 unfolding

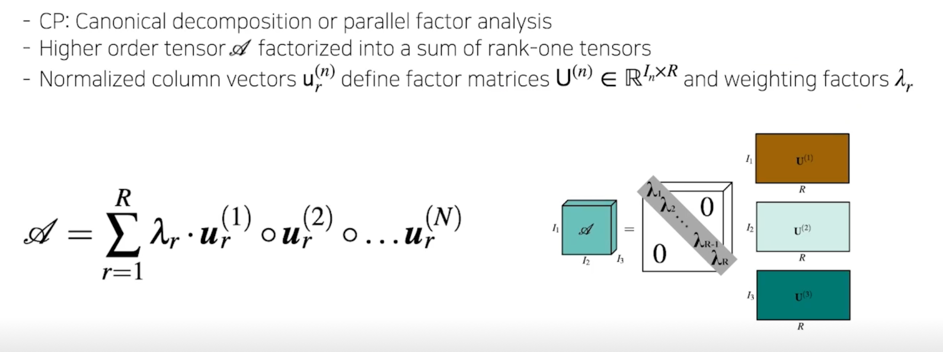
1.2 CP, Tucker decomposition

CP decomposition: concept

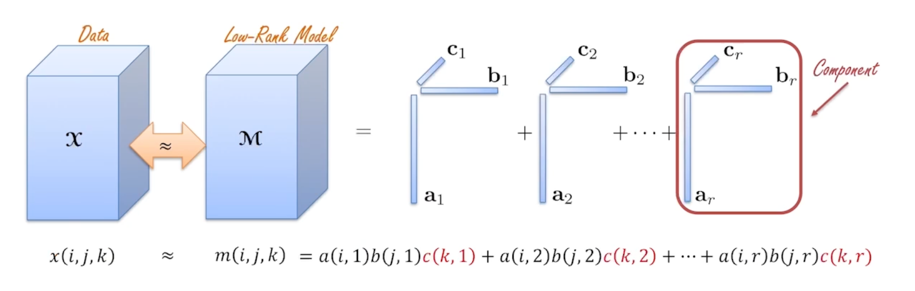
CP decomposition: summary

Tucker decomposition

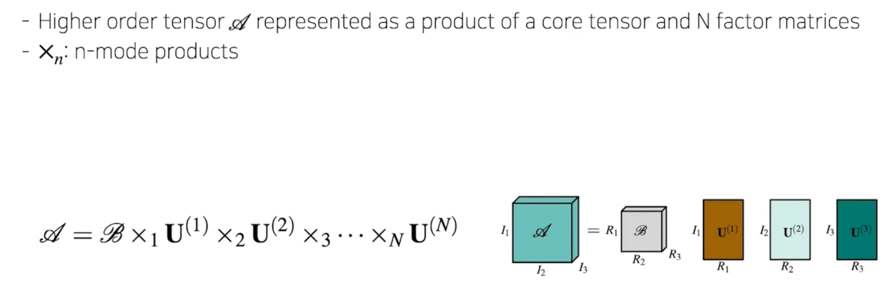
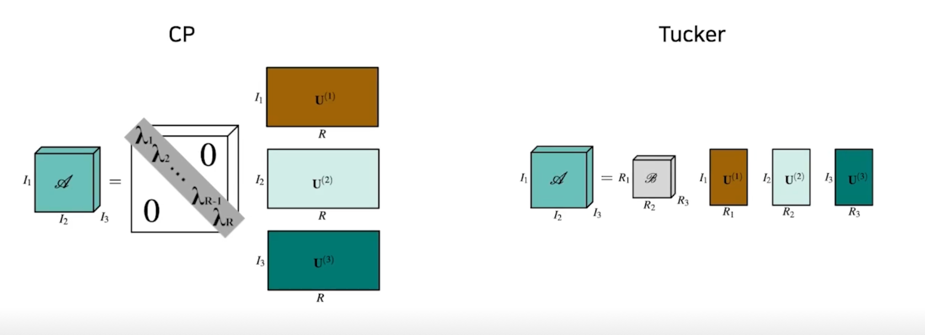
CP is one of special case of Tucker decompostion

2. Tensor operation with TensorLy

2.1 TensorLy 소개

TensorLy

• Tensor decomposition, tensor learning, tensor algebra 등을 수행해주는 Python library
• NumPy, PyTorch, JAX, MXNet, TensorFLow, CuPy 등의 라이브러리 들과 호환하여 활용 가능
• 쉬운 사용성

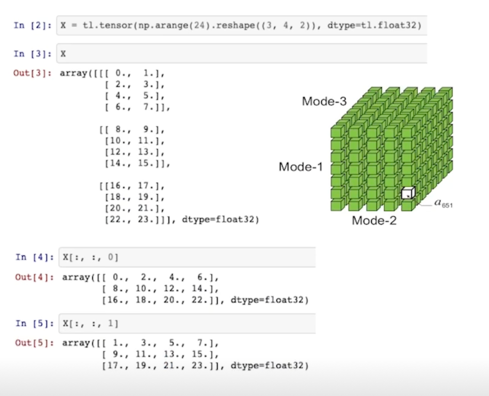
텐소 표현

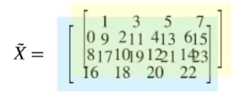
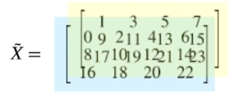
• (3, 4, 2) dim 을 가지는 텐서 $\tilde{X}$
• $\tilde{X}$ 의 frontal slices 를 $X_1, X_2$ 라 할 때,

2.2 Tensor Operation 실습

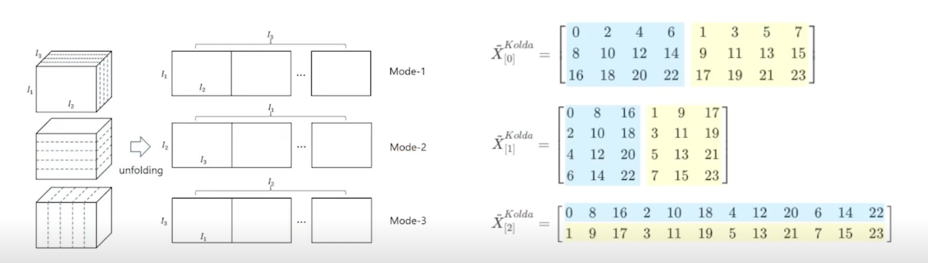
Tensor unfolding; 일반적인 방법

• 정의 과정에서는 1-index 를 사용하여 (1, 2, 3 - mode)로 표현하엿으나, code 에서는 python 0-index 로 표현(0, 1, 2 - mode)
• 앞 슬라이드의 $\tilde{X}$ 에 대하여, 0, 1, 2 - mode unfolding 은 각각 아래와 같이 표현

Tensor unfolding; TensorLy 의 방법

• TensorLy 에서는 n-mode unfolding 의 방향을 다르게 정의함
• 이는 unfolding 과정이 C-ordering 으로 수행되어 더 빠르고 효율적으로 수행되게 함
  (better cache performance)
• 기존의 방법은 Fortran-ordering

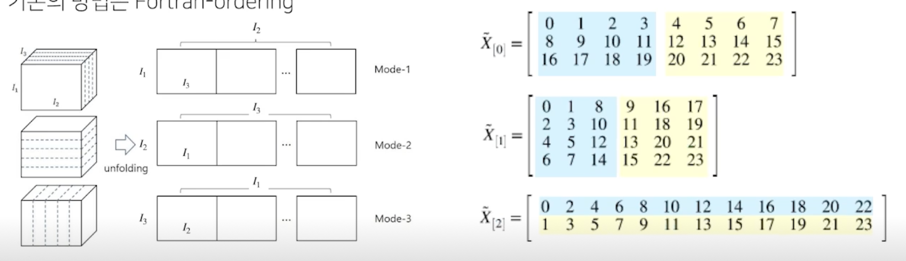
쌓이는 방향이 좀 다름

참고자료

• Numpy 공식문서에서의 C, Fortran order 에 관한 논의
  https://numpy.org/doc/stable/reference/internals.html#internal-organization-of-numpy-arrays
• C vs Fortran memory order
  visitusers.org/index.php?title=C_vs_Fortran_memory_order

• Tensorly 의 unfording 설명
  http://jeankossaifi.com/blog/unfolding.html

• 코드 상에선 unfold 함수로 쉽게 연산 가능

n-mode product

• Tensor 를 matrix 또는 vector 와 곱할 때, mode n 으로 연산하는 것
• Given a tensor $\tilde{X}$ of size$(I_1, I_2, …, I_N)$, and a matrix $M$ of size $(D, I_n)$, the $n$-mode product of $\tilde{X}$ by $M$ is written $\tilde{X} \times_n M$.
• n-mode 에 대응되는 Slice 로 표현하여 각 matrix multiplication 처럼 연산
• Example) $\tilde{T}$ : (2, 2, 2) tensor, $M$ : (3, 2) matrix

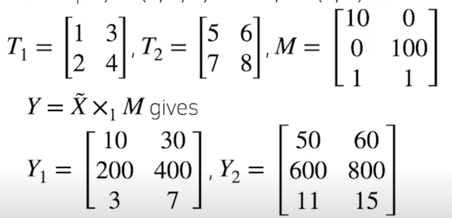
n-mode product; TensorLy

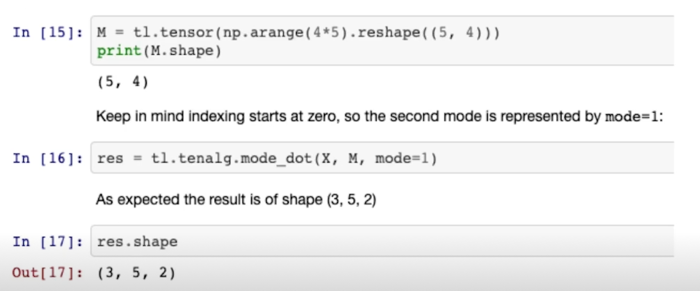
• $X$ 의 size 를 (3, 4, 2)라 하고, size (5, 4)인 matrix $M$ 이 있다고 할 때, 1-mode product 는 아래와 같이 연산 가능

CP decomposition

• TensorLy 내에 parafac 함수

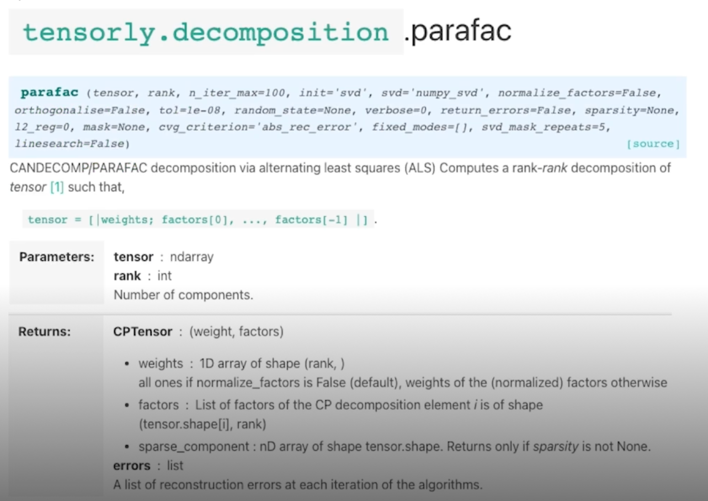
• weights : 앞에서 설명한 $\lambda$ 값들
• factors : tensor shape 와 matrix 들로 tensor 가 나옴

Tucker decomposition

• TensorLy 내에 tucker 함수

2.3 CP, Tucker decomposition 실습

CP, Tucker decomposition; 코드

연산하는 과정을 보여주려 함

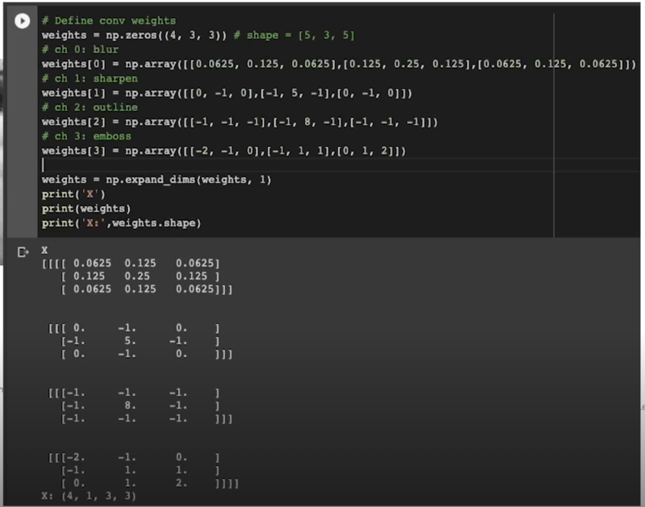
CP decomposition; 코드

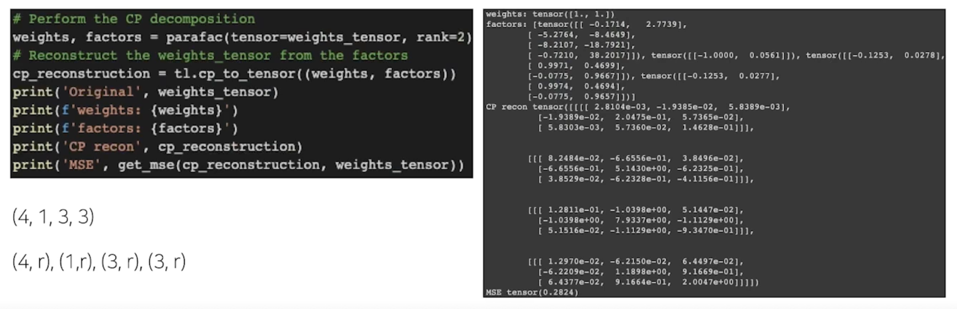
weights 같은 경우는 normalize option 을 주지 않았기 때문에 $\lambda$ 값 자체가 다 그냥 tensor 안에 들어가버렸음

weight 로 normalize 되어서 $\lambda$ 가 빠져나온게 아니라 $\lambda$ 가 곱해져 있는 형태로 되어있음

Tucker decomposition; 코드

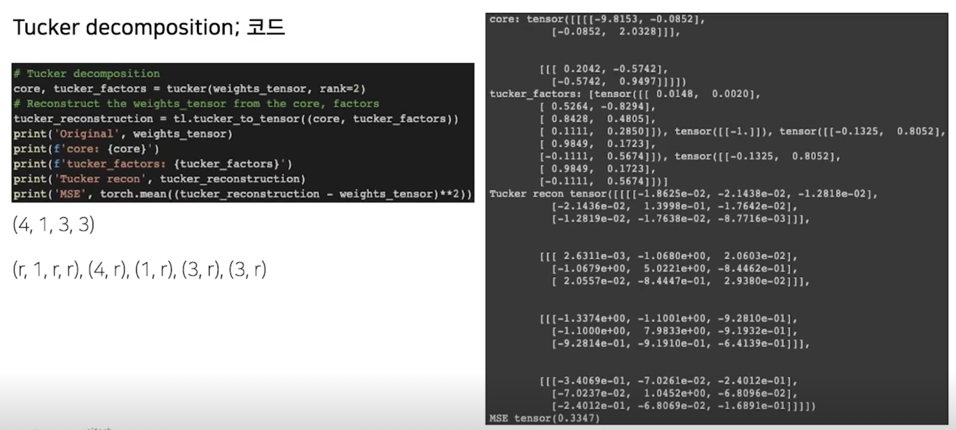
3. Tucker decomposition on Conv layer

3.1 Tucker-2 decomposition

Tucker-2 decomposition

• 참고 논문: Kim, Yong-Deok, et al. “Compression of deep convolutional neural networks for fast and low power mobile applications.” arXiv preprint arXiv:1511.06530 (2015).
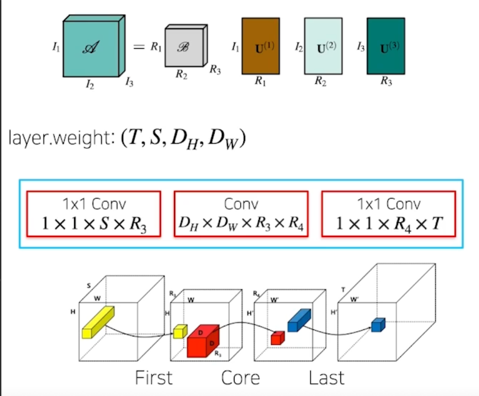
• $D_H \times D_W \times C_{in} \times C_{out}$ dim 을 가지는 conv 의 경우 일반적으로 $D_H, D_W$(kernel size)의 크기가 작으므로 (3, 5), kernel size 에 해당하는 dim 의 경우, core tensor 의 크기를 원 tensor 와 동일하게 유지함

$U^{(3)}$ 의 크기는 $S \times R_3$ 가 되고 $S$ 는 input 의 channel 개수라고 보면 되고 $R_3$ 는 그것에 대해서 approximation 하려는 Rank 의 차원수 혹은 값이 될거고 $T$ 같은 경우는 output channel 의 개수가 될 거고 $R_4$ 같은 경우는 그 output channel 에 대해서 approximation 하려고 하는 Rank 의 개수 혹은 차원수가 될 것이고 $C$ 는 $D \times D \times R_3 \times R_4$ 가 될 것임

Decomposition

• $D_H \times D_W \times C_{(in)} \times C_{(out)}$ dim 을 가지는 Conv 를
  $1 \times 1 \times C_{(in)} \times R_1 \rightarrow D_H \times D_W \times R_1 \times R_2 \rightarrow 1 \times 1 R_2 \times C_{(out)}$ 3단계의 Conv 로 decompose

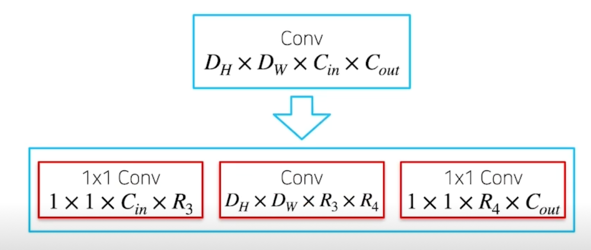
Decomposition; figure

Params, Flops 변화

Params, Flops 변화; 예시

• $3 \times 3 \times 64 \times 128$ dim 을 가지는 Conv 를 rank=32 로 decompose
  $1 \times 1 \times 64 \times 32 \rightarrow 3 \times 3 \times 32 \times 32 \rightarrow 1 \times 1 \times 128 \times 32$
• Params 비교
  Original: $3 \times 3 \times 64 \times 128 = 73728$
  Decomposed: $32 \times 64 + 3 \times 3 \times 32 \times 32 + 32 \times 128 = 15360$
• Flops 비교
  input feature map: (64, 100, 100) 가정
  Original: 1414.94 MFlops
  Decomposed: 40.32 + 176.71 + 162.56 = 379.59 MFlops

Flops 는 GPU 연산에서는 성능 혹은 추론속도에 영향을 주는 major 한 요소가 아닌 것 같음

그렇지만 CPU 상에서 inference 를 돌리는 상황에서는 Flops 가 GPU 대비해서는 더 큰 factor 중 하나이기 때문에 CPU 로 연산을 하는 환경에서는 major 한 영향을 줄 수 있음

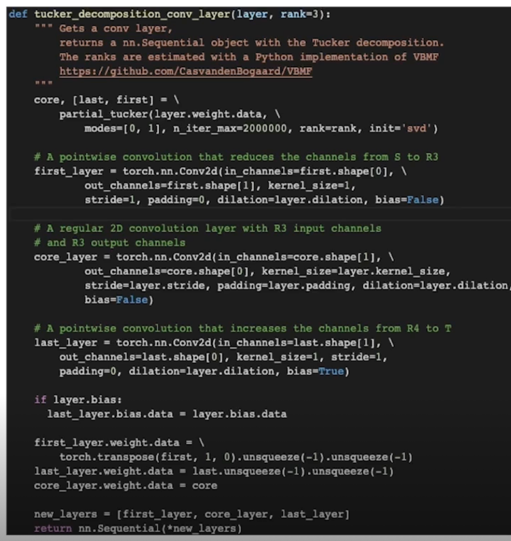
tucker-2 decomposition 을 사용하려면 partial_tucker 함수를 사용해야 함

왜 mode=[0, 1] 이냐고 한다면 layer 의 weight 같은 경우에 PyTorch 의 경우에는 dimension 의 배열이 앞선 예시와 다름

그래서 output channel, input channel, kernel 의 크기로 정의가 되기 때문에 kernel 의 대한 차원은 decompositoin 을 하지 않고 input, output 차원에 대해서만 decomposition 을 한다고 했기 때문에 mode=[0, 1] 이 들어감

4. Finding rank using AutoML

4.1 주어진 모델(vgg16) 잘게 찢기

Rank 설정의 어려움

• Tucker Decomp 를 NN 에 적용하는 경우, 각 레이어(또는 모듈) 갯수 만큼의 파라미터(rank)를 결정해주어야함
• 앞선 논문에서는 Variational Bayesian Matrix Factorization (VBMF)라는 방법을 적용하여 rank 를 추정하였음
  • VBMF 라는 방법이 잘 되지만 항상 잘된다는 보장은 없으니
• AutoML 로도 rank 들을 결정할 수 있음

주어진 모델(vgg16)

• vgg16 을 cifa10 에 맞게 변형

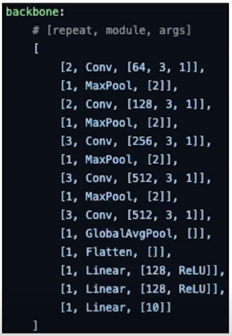
Search space

• 기존의 $R_1, R_2$ 가 아닌 $R$ 단일 파라미터로 decompose 를 수행
  $1 \times 1 \times C_{(in)} \times R \rightarrow D_H \times D_W \times R \times R \rightarrow 1 \times 1 \times C_{(out)} \times R$
• 각 모듈 레벨(conv + repeat)에는 동일한 rank 를 적용
• Output channel 을 기준으로 normalized 된 rank 파라미터를 사용
  ex) in: 64, out: 128, rank=0.25 인 경우, rank = 128 * 0.25 = 32

4.2 구현

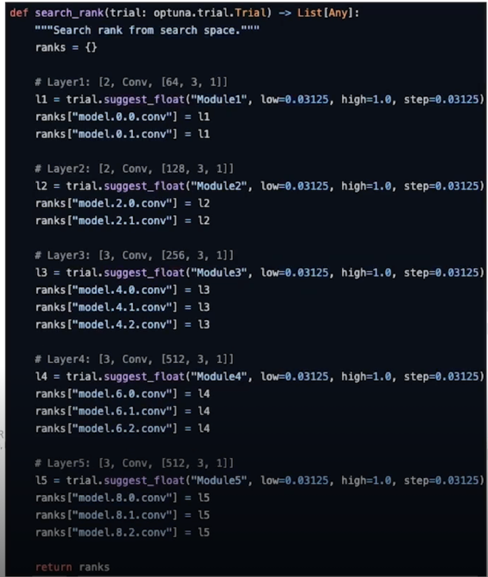
Register buffer

• 각 conv layer 에 rank 값을 register_buffer 를 활용하여 assign

Search space

• 각 rank 는 1/32 ~ 1, step: 1/32 에서 sample

4.3 실험 결과

실험 결과

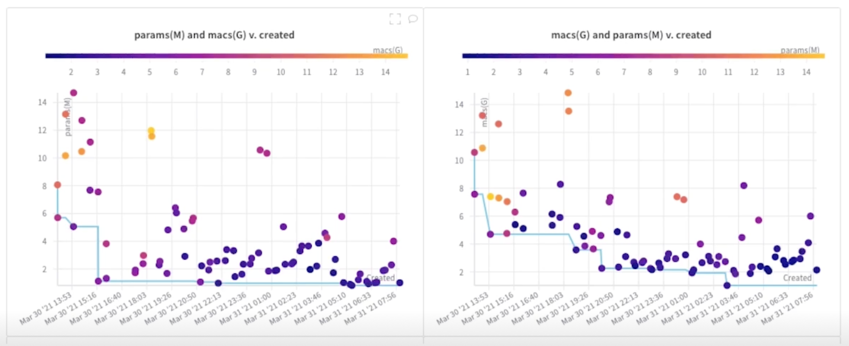
더 적은 Flops 를 찾아가는 걸 볼 수 있음

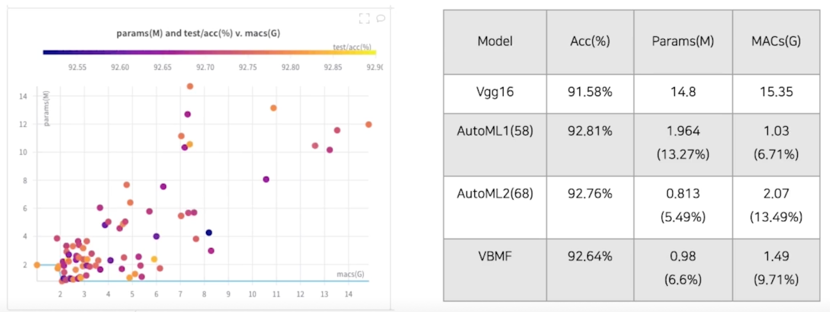
성능도 1% 가량 좋아지고 Params 도 1/10 로 줄어들고 MACs 도 1/10 로 줄어듦

Search 하는게 만능은 아니고 여전히 수학적인 approach 가 많이 유의미하고 이것들에 대해서 많이 숙지하는게 시간을 절약하고 많은 도움이 될 수 있음

4.4 논의

더 이야기 드리고 싶은 내용

• 대회 점수에 큰 영향을 줄 것으로 예상되어, baseline 코드에는 코드를 공개하지 않았습니다
  • A. Rank 를 시도해보는 구현을 다양하게 시도해주세요!(성능을 끌어올리는 search space)
  • B. 다양한 architecture 들에 대해서 일반화하여 적용하려면?
• Architecture search $\rightarrow$ Rank search 의 과정을 꼭 거쳐야 할까?
• Flops 는 속도에 영향을 주는 요소 중 하나일 뿐, indirect 한 metric 에 불과함
  (CPU, GPU 등 device 에 따라 속도에 기여하는 정도도 다름)

Reference

Further Reading

• jacobgil/pytorch-tensor-decompositions
  • PyTorch implementation of [1412.6553] and [1511.06530] tensor decomposition methods for convolutional layers.
• Accelerating Deep Neural Networks with Tensor Decompositions
  • My PyTorch implementation for tensor decomposition methods on convolutional layers. Notebook contributed to TensorLy.
• Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications