Day_81 01. 찾은 모델 잘게 찢기: Tensor Decomposition 이론
작성일
찾은 모델 잘게 찢기: Tensor Decomposition 이론
1. 소개 & 리뷰
1.1 Tensor Decomposition?
Tensor Decomposition 을 검색하면?
간단한 tensor 들에 대해서 연산들의 조합으로 한 tensor 를 표현하는 방법
Matrix decomposition 의 tensor 버전
Tensor utilized in many area[2]
- Chemometrics: Emission x Excitation x Samples
- 화학측정학문분야
- Neuroscience: Neuron x Time x Trial
- Transportation: Pick-up x Drop-off x Time
- Signal Processing: Sensor x Frequency x Time
- Social Network: User x User x Time x Interaction-Type
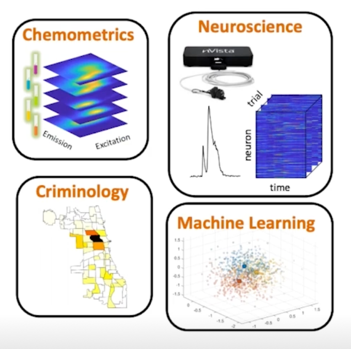
2-dimensional 이상의 데이터들은 Tensor 로 표현된다고 보면 됨
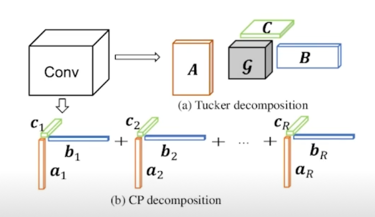
강의에서 살펴볼 두가지 방법
용어를 살펴봅시다
CP decomposition 이라고도 함
SVD 를 Tensor 버전으로 generalize 했다고 봐도 됨

CP decomposition 의 약간의 더 generalize 된 버전임
원래 diagonal tensor 로 표현되던게 일반 core tensor 로 표현되는게 Tucker decomposition 이라고 함
1.2 Review: SVD
Singular Value Decomposition(SVD)
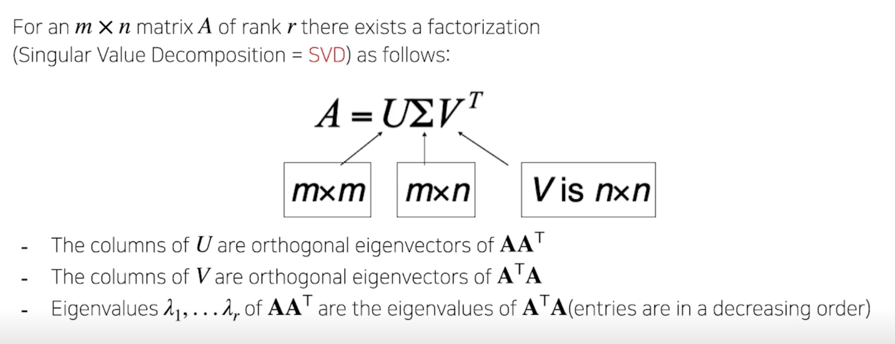
$AA^T$ 와 $A^TA$ 의 eigenvalue 들이 같고 그게 $\sigma$ 에서의 어떤 diagonal matrix 내에서 각 component 들이 됨
가장 큰 값이 첫번째로 들어오고 감소하는 순서로 배열이 되어 있음
A 가 m x n matrix 라고 했을 때, U matrix 는 m x m 이 되고 $\sigma$ 의 경우는 m x n, V 같은 경우는 n x n 이 됨
SVD as Sum of Outer Products
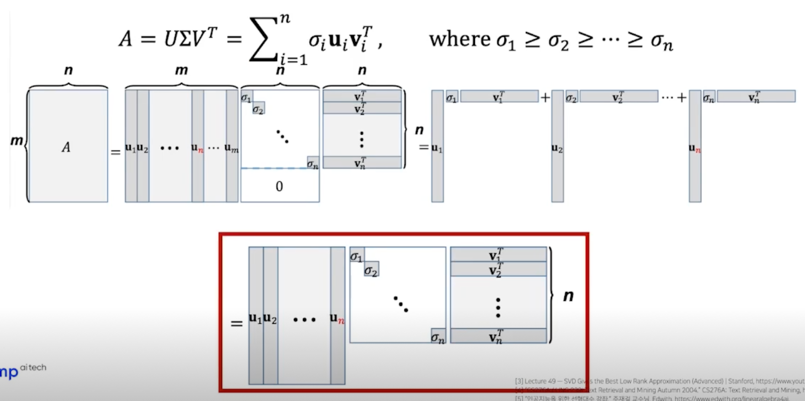
SVD can be used to compute optimal low-rank approximations
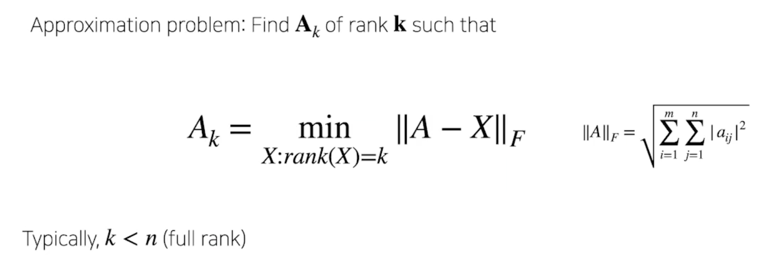
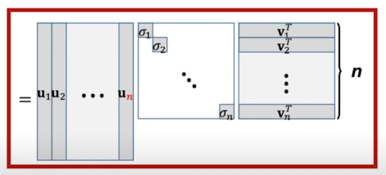
위 그림이 A 의 Full rank matrix 라고 하면 여기에서 k 개 만큼 rank 를 설정하게 되면
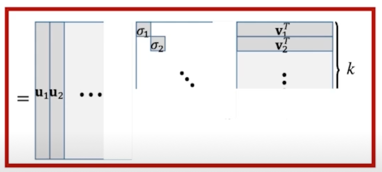
그림처럼 k 개 만큼 잘라서 사용하게되면 그게 approximation 의 해가 됨
SVD 가 이 문제를 해결하는데 solution 으로 활용될 수 있다고 보면됨
1.2 SVD: Application
Image Compressions Example

singular value 들이 크기순으로 배열되어있고 크게 기여하는 상위 몇개들만 사용하게되면 왼쪽에 있는 이미지를 표현할 수 있다라는게 Image Compression 에서의 아이디어임
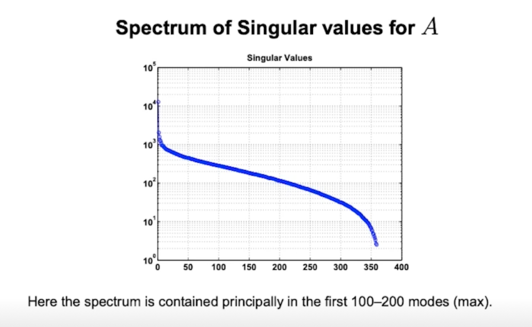
spectrum 이라고 적혀있지만 $\sigma$ 의 값들을 정렬해놓은거라고 봐도 무방함
앞에있는 몇개의 가중치들이 뒤에있는 대부분의 합보다 훨씬 더 dominant 하게 영향을 준다고 보면 됨
100~200개 정도의 eigen value 들만 사용해서 rank k 개만 k 가 100~200개 mode 를 가지는 그정도의 k 만 설정해서 compression 을 수행해도 원래 이미지가 표현하려던 것의 대부분의 정보를 표현할 수 있다라는걸 이야기 하고 싶은 것

맨처음에 rank 1 으로 decomposition 을 해보면 오른쪽 그림과 같은 결과가 나옴
각 칸 안에 숫자들이 있는데 rank 1 만으로는 칸정도만 표현

rank 10 으로 표현하게되면 흐릿흐릿하지만 점점 숫자들이 표현이 되게 됨
10개만 쓰게되면 원래 pixel 개수보다 5%만 사용하게 됨

20개 ~ 30개 갈때 흐릿흐릿하게라도 점점 숫자들이 보임
40개되면 거의 다 식별이 가능한 정도가 됨
50개 정도가 되면 색의 명도차이만 있을뿐 안에들어가는 내용들은 충분히 구별이 가능한 상태임

100개와 200개를 봤을 때 거의 유사한 결과를 보여줌
matrix 에서 가장 큰 영향을 주는 요소들로 SVD 가 정렬이 되어있기 때문에 상위의 mode 들만 선택하더라도 원래 표현하고자 하는 의도의 이미지를 표현할 수 있게되고 이런식으로 이미지를 compression 할 수 있다
2. Tensor Decomposition
2.1 Basic notation
Vector Outer Products
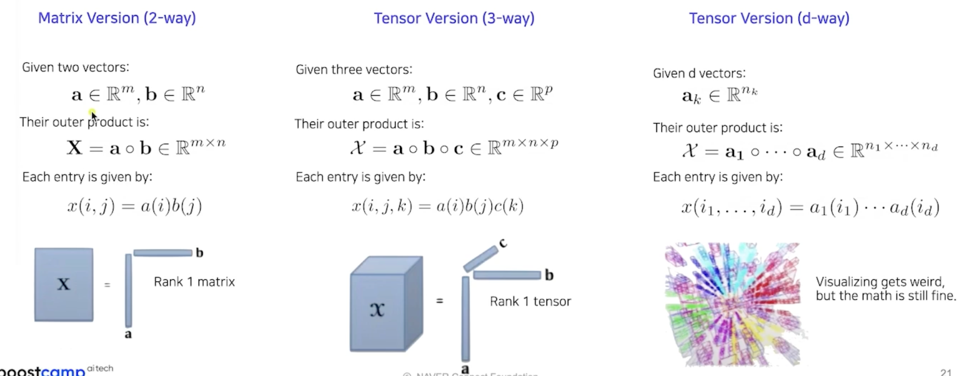

2.2 CP Decomposition
Detecting low-rank 3-way structure(heavily borrowed from [7])
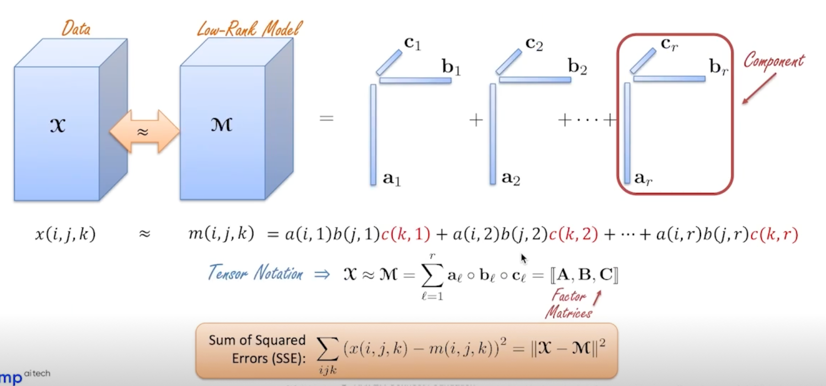
Tensor Decomposition 은 데이터를 low-rank model 로 approximation 할 때 많이 썼던 것임
우리는 weight matrix 를 decompose 하는 것이기 때문에 데이터처럼 dimension 이 크지는 않지만 원래 의도는 데이터였기 때문에 데이터로 표현된걸 볼 수 있음
그렇지만 하는 과정은 동일함
Fitting CP: hardships(heavily borrowed from [7])
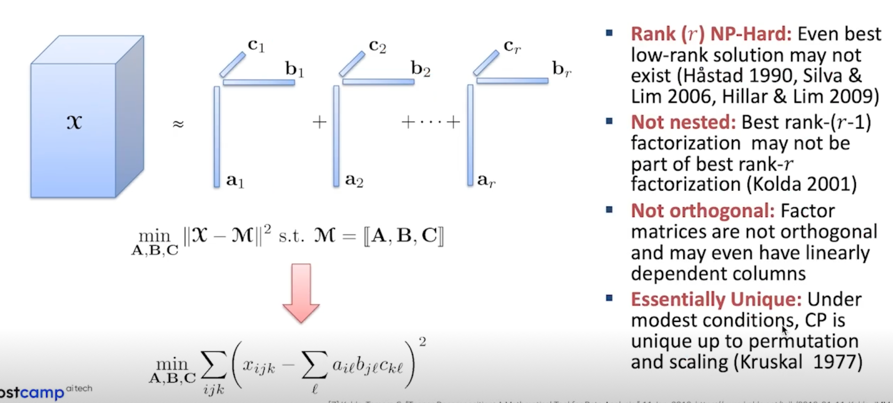
CP 혹은 Tensor 로 넘어오면서 오른쪽과 같은 문제들이 발생
- Best low-rank solution 이 존재하지 않을 수 있다. 존재성이 증명되어있지 않음
- rank r 일 때의 CP Decomposition 을 수행하고 싶은데 더 작은 rank 들에 대해서 계산을 하고나서 거기서 확장시켜서 더 큰 rank 들을 계산해보자
rank r-1 을 계산한다음에 거기서 하나를 추가해서 rank r 을 만들어보자라는 생각을 당연히 할 수 있을텐데 이게 그렇게 되지 않는다라는 것임
rank r-1 에서 Best rank 했던 factorization 은 rank r 의 어떤 부분이 아닐 수 있다라는 것임 - 컬럼들이 orthogonal 하지 않고 linearly dependent 할 수 있음
- CP 는 permutation 과 scaling 에 대해서 unique 한 성질을 가지고 있음
Fitting CP: ALS(Alternating Least Square)(heavily borrowed from [7])
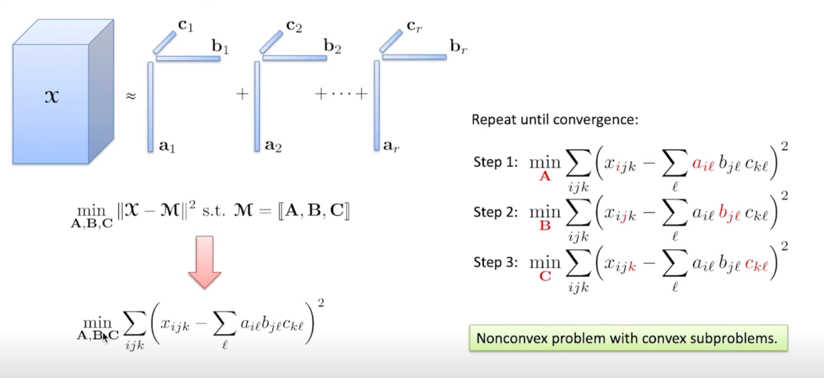
3차원 tensor 같은 경우에는 component 가 3개가 있는데 component 1개를 계산할 때 나머지 2개를 고정시켜놓고 하나에 대해서 Least Square 문제를 풀고 이게 step 1 이 되고 A 빼고 나머지에 대한 matrix 를 고정해놓고 A 를 minimize 하는 방향으로 Least Square 문제를 풀고 그 다음 step 에서는 A 와 C 를 고정시켜놓고 B 를 Least Square 문제 풀고 다음은 A 와 B 를 고정시켜놓고 C 를 minimize 하도록 Least Square 를 풀고 이걸 반복적으로 수행하는게 방법임
안에들어가는 subproblem 들은 Least Square 니까 convex 할테고 이걸 각 component 에 대해서 곱으로 정의가 되어있기 때문에 실제로는 Nonconvex 한 문제임
그렇지만 안에 들어가는 problem 들은 convex 라고 표현하게됨
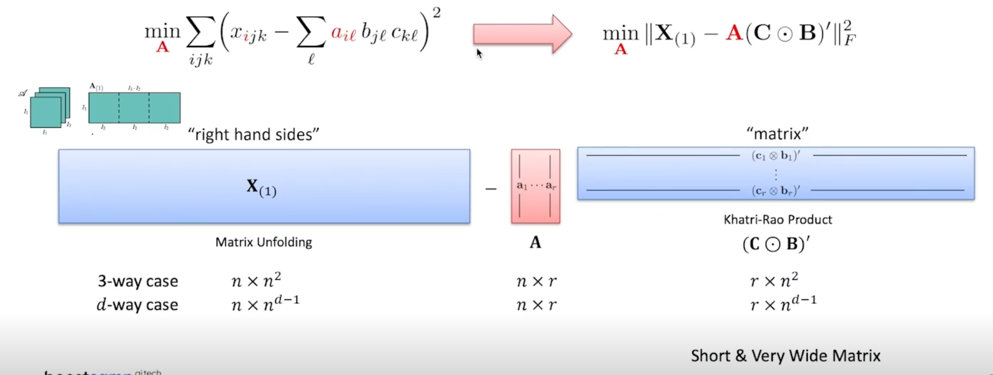
$X_{(1)}$ 은 Matrix Unfolding 을 한 형태
Fitting CP: Simple code with torch
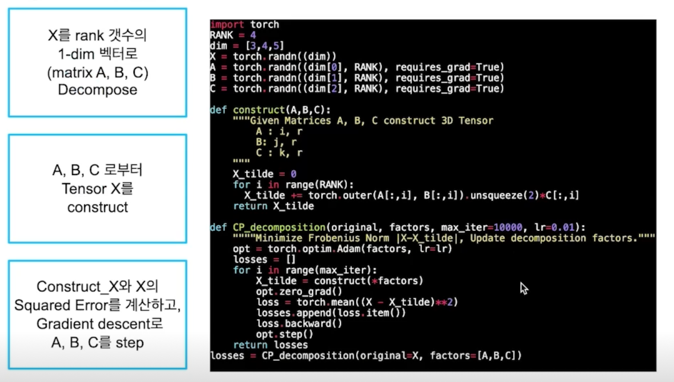
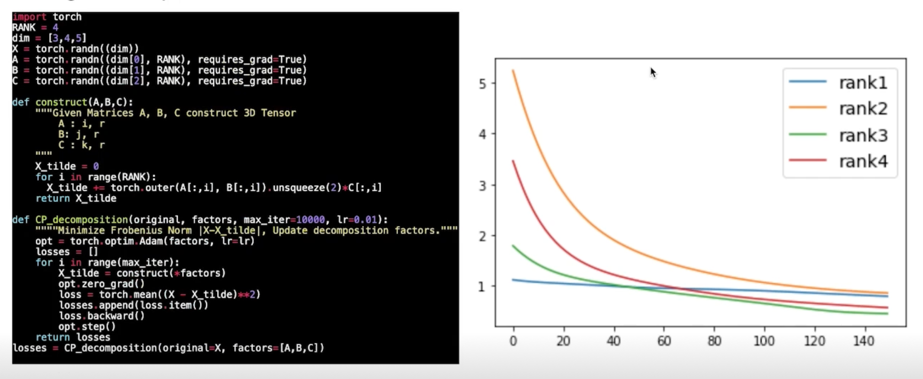
Summary

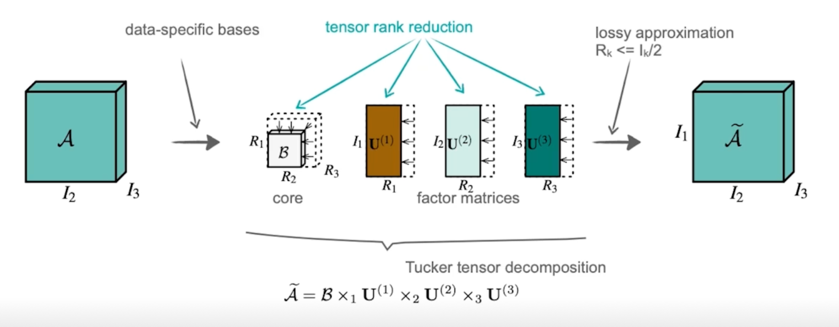
2.3 Tucker decomposition
Summary

diagonal tensor 가 아니라 좀 더 일반화된 core tensor 로 변화가 됨
tensor 와 matrix 의 곱을 정의해야하기 때문에 n-mode products 라는 concept 이 들어옴
mode 를 axis 로 봐도되고 tensor 가 여러 축을 가지고있으니까 축과 matrix 의 어느 축을 연산할건가에 대한 notation 이라고 보면 무방할 것 같음
Rank reduction with Tucker
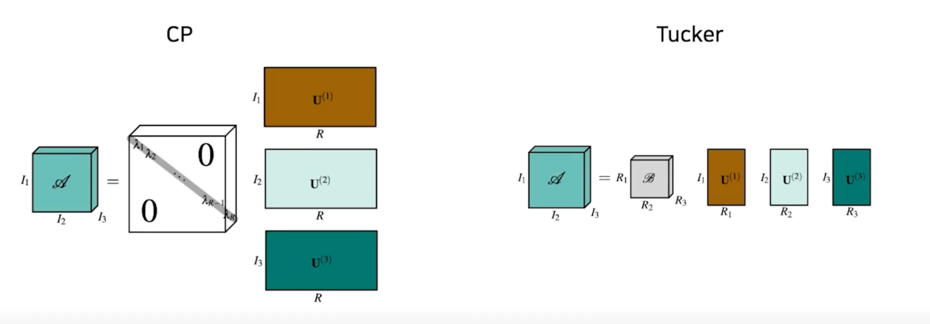
CP is one of special case of Tucker decomposition
3. Tensor Decomposition: 실습 예제
3.1 Toy example: hand-crafted conv weights
Decomposing Conv block: 실습 목적
- DL 에서의 Decomposition 은 데이터를 decompose 하는 것이 아닌, 네트워크의 weight 를 decompose 하는 것
- Conv block(Tensor)를 decompose 했을 때,
- decompose 전의 feature map output 과 decomposed 된 모듈의 feature map output 은 동일할까?
- 다르다면 어떻게 다를까? Rank 는 어떤 식으로 정해야할까? 에 대한 맛보기

3.2 CP decomposition MSE error(Image)

Rank 1 의 경우 차이가 큼
Rank 3 정도되면 거의 비슷함
3.2 CP decomposition MSE error(value range)
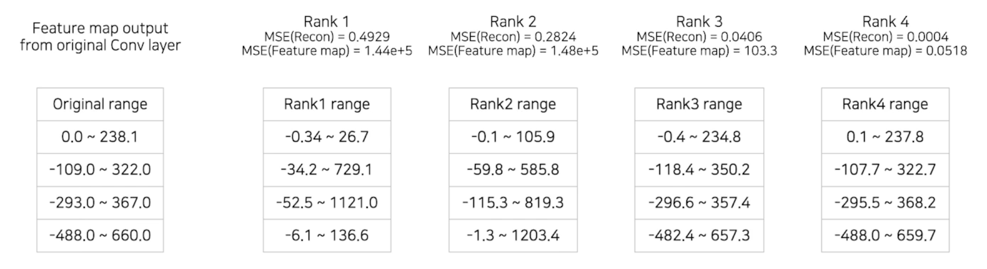
Rank 3 부터는 Reconstruction 값이 비슷하게 mapping 되는 걸 볼 수 있음
3.3 Tucker decomposition MSE error(Image)

Tucker decomposition 에서도 거의 비슷한 결과를 보여줌
3.3 Tucker decomposition MSE error(value range)
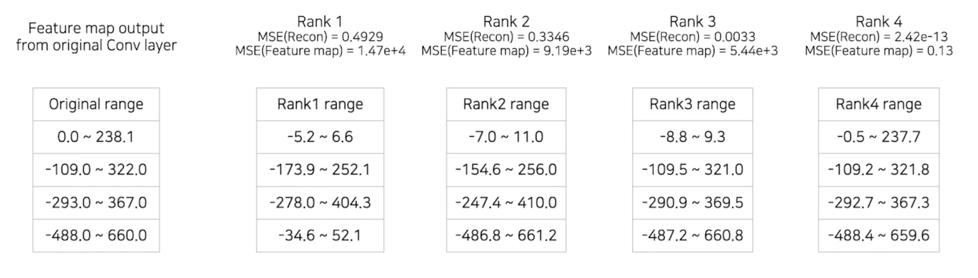
똑같이 value range 가 벌어짐
3.4 CP, Tucker range comparison
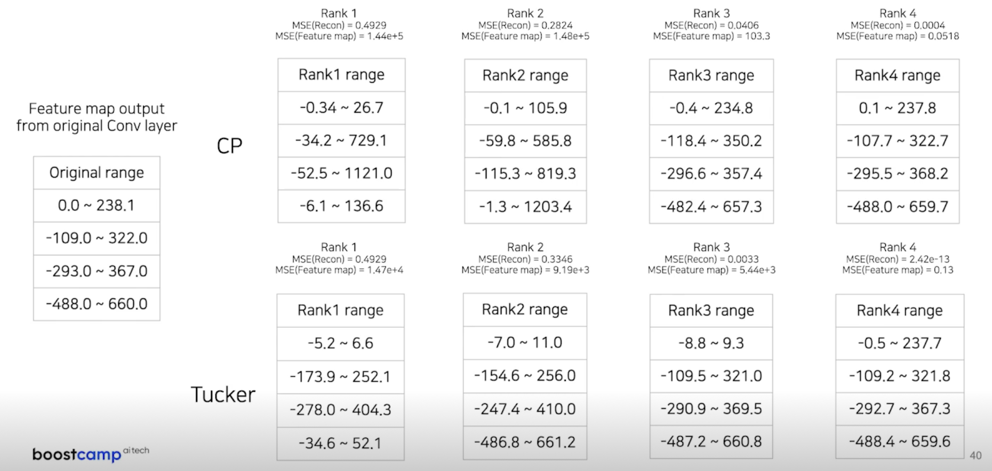
누가 좋다라는걸 얘기하고 싶은건 아니고 결과를 보면서 생각을 해봤으면 좋겠다
Rank 가 제대로 맞지 않으면 엉뚱한 feature 를 뽑아냄
3.5 정리
실험 결과로 엿보는 한계와 논의
- 적절한 rank 설정의 중요성
- 원래 conv layer 가 뽑는 feature 를 유사하게 뽑아내는 decomposition 이 가능
- 헌데, 일반적으로 fine-tuning 이 수반되는데, 그렇다면 원 feature 를 유사하게 뽑아내는게 중요하긴 할까?
- rank 만 잘 잡으면, fine-tuning 이 필요 없을까?
- 적은 rank 에 대해서 값의 범위가 크게 변하는 문제를 어떻게 handling 할까?
- Batchnorm parameter 또한 함께 고려할 수 있을까?
- 값의 범위가 바뀌는 이유가 무엇일까?

댓글남기기