Day_82 01. 찢은 모델 꾸겨 넣기: Quantization 이론
작성일
찢은 모델 꾸겨 넣기: Quantization 이론
1. Quantization 소개
Quantization(signal processing)
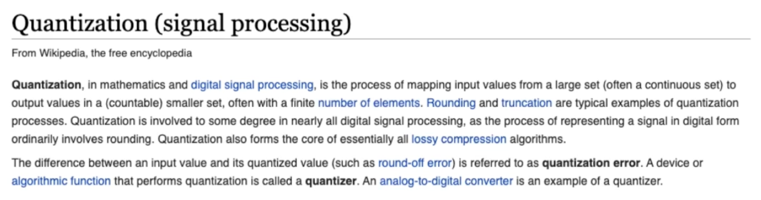
Mapping input values from a large set to output values in a smaller set
Quantization(signal processing); 예시
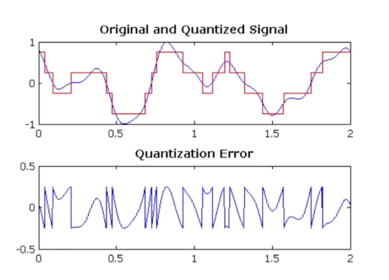
2bit(4개, -0.75, -0.25, 0.25, 0.75)으로 신호를 표현
Quantization Error(Original - Quantized)는 최대 “구간 간격의 절반”이 됨
- 원래 신호에 대해서 Quantized 신호를 빼게되면 손실이 발생할건데 그 에러의 경우에는 최대 구간 간격의 절반이 됨
- 원본 시그널과 Quantized 된 시그널의 차이를 보면 결국 최대 -0.25에서 0.25사이에 Mapping 이 되는걸 볼 수 있음
1.1 Introduction
Neural Network 에서의 Quantization?; 현실적인 Motivation

생각을 따라가보자! Weight 분포 분석
- 2015년에 나온 Inception v3 model 의 첫번째 conv layer 의 weight 분포
- 256개의 bin 을 가지는 histogram 으로 plot
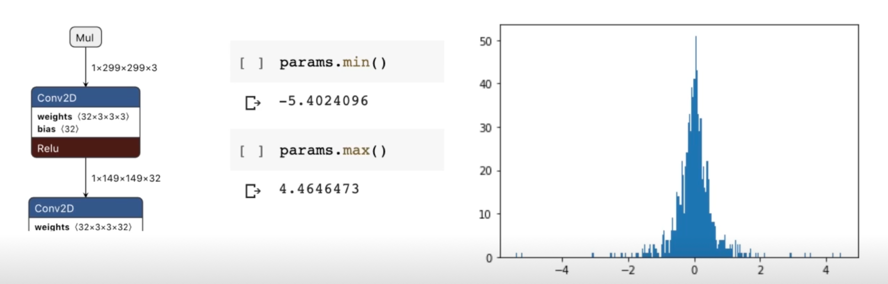
histogram 을 관찰해보면
- 0 근처에서 촘촘하고, 대체로 0기준 대칭인 경향
- 2.0 이상의 값은 그리 많지 않음
- 대부분의 histogram slot 은 비어있음
생각을 따라가보자! Bit encoding
- 기존의 32bit float 값을 8bit int(256개의 bin)으로 Fixed point mapping(encoding)하면 어떨까?
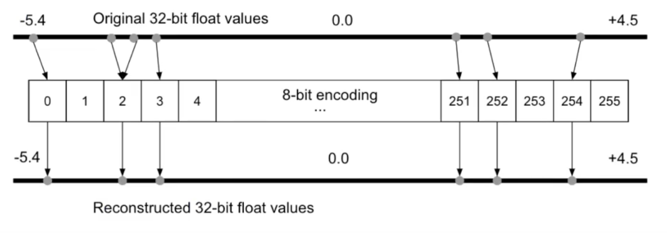
실제로 코드로 구현해보면

Quantization Error(Original weight - Quantized weight)는 최대 “구간 간격의 절반”, +/-((max-min)/256)/2 $\approx$ 0.02
Happy Ending
- 당시에는 연구 관점보다는 Engineering 으로의 접근이 대부분
- 이 후에 연구가 활발하게 진행

용량을 1/4로 줄이면서 그러면서 accuracy 에는 영향이 별로 없었고 그로인해 스마트폰에 잘 deploy 할 수 있었다
1.2 Quantization 의 이점
모델 사이즈를 줄여주는 것은 알겠어, 그 밖에는?
- 일반적인 필터 연산 과정 : Input * weight (+bias) $\rightarrow$ activation
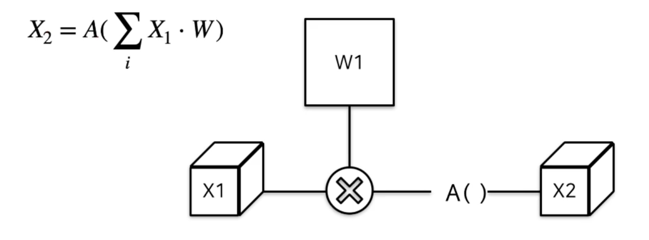
- 하드웨어에서는 MAC(Multiply-Accumulate) unit 을 통하여 해당 연산을 수행
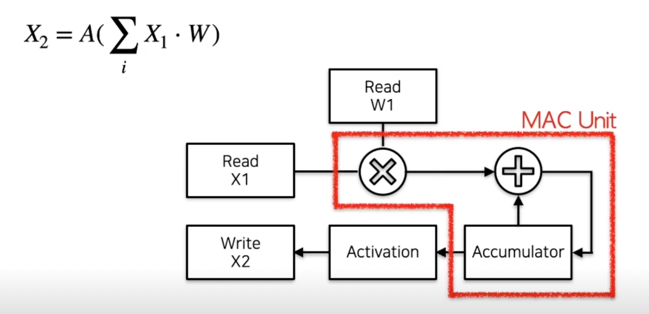
- 에너지 소비 관점에서도 Fixed point quantization 이 유리
FP32(Mult + Add): 4.6(pJ) // Int8(Mult + Add): 0.23(pJ)
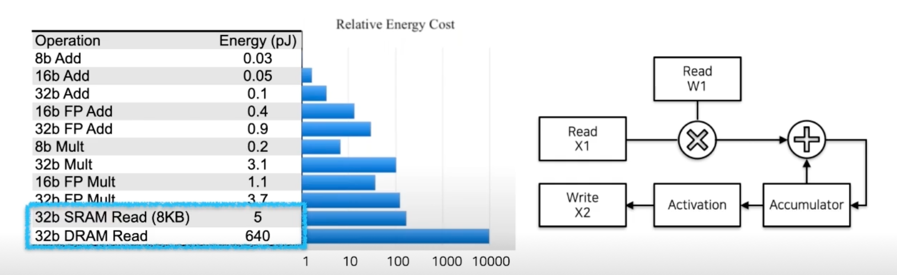
대신에 이런 Relative Energy Cost 를 봤을 때 연산하는것보다 램에서 읽어오는게 훨씬 더 Energy Cost 가 많이듦
그래서 줄여봐야 Read 하는 부분에서 Energy Cost 를 다 먹는거 아니냐고 얘기할 수 있는데
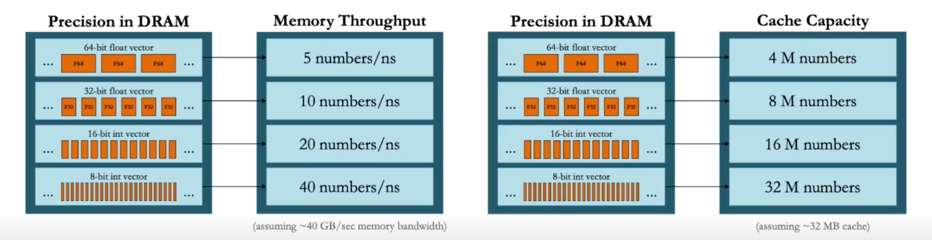
- 외부 메모리 접근의 높은 Cost
- But, 한번에 읽어오는 크기도 늘어나므로(x4 bandwidth), 더 효율이 좋아짐
NN 에서의 Quantization
- 기존의 high precision(일반적으로 fp32) Neural network 의 weights 와 activation 을 더 적은 bit(low precision)으로 변환하는 것
- 일반적으로 fp16, int8 등이 많이 사용됨
2. Quantization 이론
2.1 Fixed point & Floating point
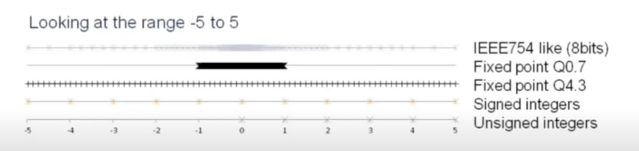
수 표현의 방법: 1) Fixed point(32bit)
- 등간격으로 수를 표현
- 항상 동일한 해상도를 가짐
- Ex) m=8, n=24, Range: -128 to 127, Resolution: $1/2^24$

수 표현의 방법: 2) Floating point(32bit)
- $\pm$ Mantissa $\times 2^{Exponent}$ 로 수를 표현
- Ex) IEEE 32-bit float
sign: 1bit, exponent(m): 8bit, mantissa(n): 23bit
Range: $-2^{126}$ to $2^{127}$ (-127; all 0, 128; all 1는 별도로 예약됨(zero, NaN, infinity))
Resolution: 가변적($2^{Exponent} \cdot 1/2^{24}$)

계산하는 과정을 살펴보자

sign 을 1bit 으로 정의했음, exponent 를 8bit 으로 봤고, mantissa, fraction 이라고 해도되는데 여기에 23bit 가 들어감
Fixed point vs Floating point
- Fixed point
상대적으로 제한된 구간(Fractional part $\uparrow$ $\rightarrow$ 표현 구간 $\downarrow$)
대신 고정된 간격 - Floating point
더 넓은 구간
대신 가변 간격(dynamic range)
추천 article: What Every Computer Scientist Should Know About Floating-Point Arithmetic

2.2 Quantization mapping
(Affine) Quantization mapping; Quantization, De-quantization process 정의
- High precision $\rightarrow$ Low precision mapping
- Mapping a floating point value $x \in [\alpha, \beta]$ to a $n$-bit integer $x_q \in [\alpha_q, \beta_q]$
- De-quantization process
$x = c(x_q + d) - Quantization process
$x_q = round(\frac{1}{c}x - d)$ - $c, d$ are variables

(Affine) Quantization mapping; $c, d$ 결정
- Mapping a floating point value $x \in [\alpha, \beta]$ to a $n$-bit integer $x_q \in [\alpha_q, \beta_q]$, e.g. [0, 255]
- Quantization process, De-quantization process
$x_q = round(frac{1}{c}x - d), x = c(x_q + d)$ - $x = \alpha$ 일때, $x_q = \alpha_q$ 를, $x = \beta$ 일떄, $x_q = \beta_q$ 를 만족해야함
$\beta = c(\beta_q + d)$
$\alpha = c(\alpha_q + d)$ - 위의 선형시스템의 해는
$c = frac{\beta - \alpha}{\beta_q - \alpha_q}, d = frac{\alpha\beta_q - \beta\alpha_q}{\beta - \alpha}$
지금까지 유도된 결과가 아래와 같음
$x_q = round(frac{1}{c}x - d), x = c(x_q + d)$, $c = frac{\beta - \alpha}{\beta_q - \alpha_q}, d = frac{\alpha\beta_q - \beta\alpha_q}{\beta - \alpha}$
- NN 에서는 floating point 의 0.0이 quantization 후에도 0을 유지하여야함

convolution 이나 flip layer 에서 zero-padding 을 하는데 quantization 이 0으로 맵핑이 안되면 zero-padding 이 zero-padding 이 아닌게 됨 어떤 값을 가지게 됨 이렇게하면 성능이 저하되더라라는 얘기가 있음
다르게 생각하면 ReLU 같은 경우도 0을 기점으로 값이 있냐 없냐가 결정이 되는건데 그런 경우에도 ReLU 자체도 의미를 가지기 때문에 실제로 뉴럴넷에서는 floating point 0.0 이 큰 의미를 가지기 때문에 Quantization 되었을때에도 0이 표현이 되어야 한다라는 언급이 되어 있음
이걸 반영을 해보자
$x_q = round(frac{1}{c} 0 - d) = round(-d) = - round(d) = - d$
$d = round(d) = round(frac{\alpha \beta_q - \beta \alpha_q}{\beta - \alpha})$ (constraint)
$d$ 가 정수여야한다라는 의미가 포함된거라고 할 수 있음
(Affine) Quantization mapping; 정리
- Quantization process
$x_q = round(frac{1}{s}x + z)$ - De-quantization process
$x = s(x_q - z)$ - s(scale): positive floating point, z(zero point): integer
$s = frac{\beta - \alpha}{\beta_q - \alpha_q}, z = round(frac{\beta \alpha_q - \alpha \beta_q}{\beta - \alpha})$ - Quantization 값의 범위를 넘지 않도록, clip 을 추가
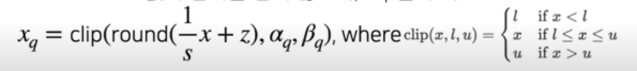
2.3 Step by step quantization
Layer 의 한 과정과정 Quantization 적용해보기
- 전체 과정에 대한 참고: [9] https://leimao.github.io/article/Neural-Networks-Quantization/
- Quantizated Matrix Multiplication - Quantization Activation - Layer Fusion
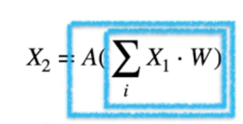
2.3 Step by step quantization; a) Matrix Multiplication
Quantized Matrix Multiplication
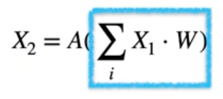
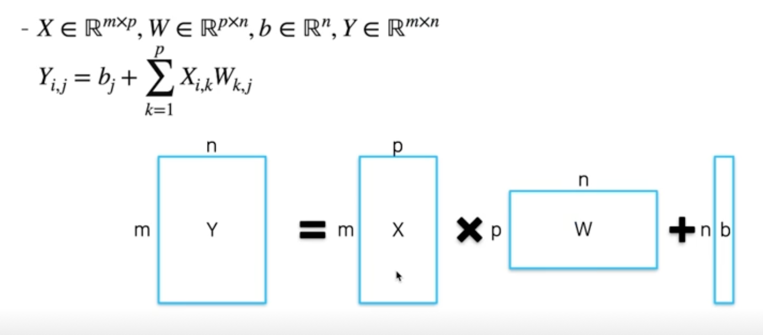
- Y 의 원소 하나를 계산하는데 필요한 연산 횟수? (bias 무시)
- vector 의 내적이 될것임
- X 의 row vector 와 W 의 column vector
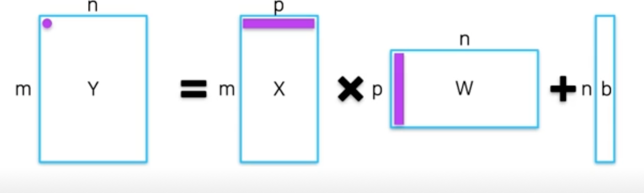
- p-dim 벡터의 내적(p 번의 곱셈, p 번의 덧셈)
- Y 를 계산하는데에는, 전체 $mpn$ 회의 곱셈, $mn(p-1)$ 회의 덧셈을 수행해야함
Quantized Matrix Multiplication; de-quantize results
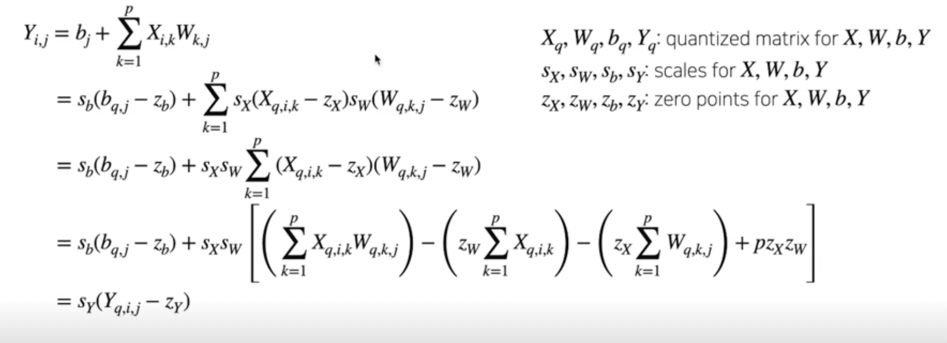
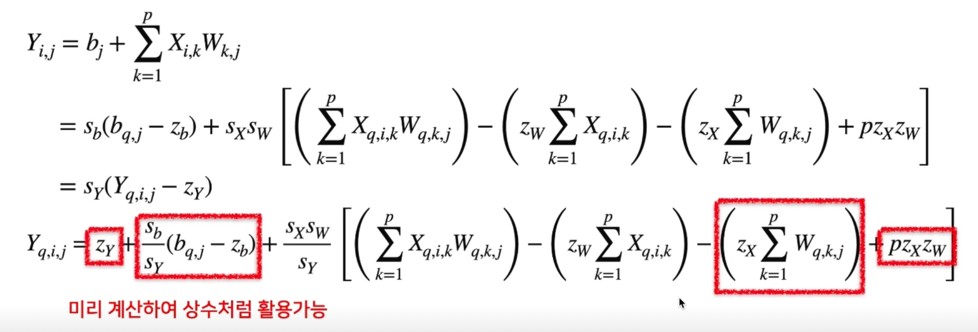
빨간색 사각형에 들어있는 부분은 inference 가 돌기전에 미리 알고있는 값들임 미리 계산해서 상수처럼 활용 가능

on-time 에서 계산하는 값들은 파란색박스 두 부분임
연산 횟수는 잠깐 늘어나지만 전력소비도 적고 대체로 속도가 빠르기 때문에 조금의 손해를 보지만 미미함
2.4 Step by Step Quantization; b) Activation(ReLU)
Quantized Activation; ReLU example
- ReLU 의 일반화된 표현
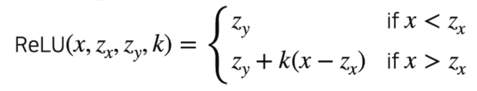
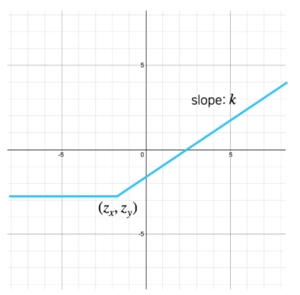
-
Example; 일반적인 ReLU
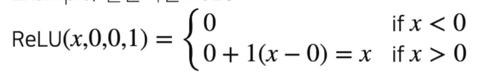
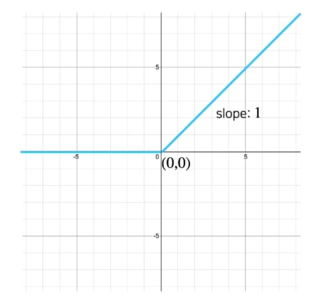
-
Deriving quantized ReLU
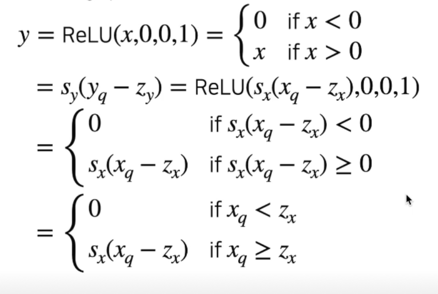
- $s_x$ 는 항상 positive 하므로
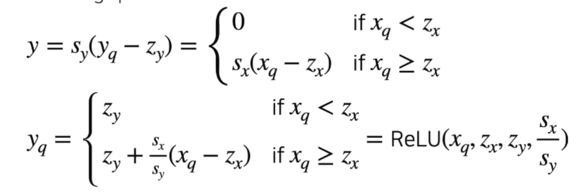

이렇게 식을 유도할 수 있음
2.5 Layer Fusion(Conv-BN)
Layer Fusion? Overview
- 학습을 더 이상 수행하지 않을 runtime 시점에, Conv layer 뒤에 추가되는 Acitvation layer, Batchnorm layer 등을 fuse 하여, 하나의 Conv layer 로 표현함
- Layer 갯수가 줄어드는 효과, 실제 inference time 에서 속도가 향상됨
- Quantization 관점에서는? Quant - decant 과정이 줄어듦(후술)
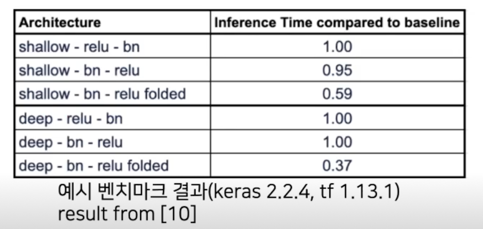
folded 가 fusion 된 결과라고 볼 때, fusion 된 결과가 layer 의 개수가 줄어드니까 inference time 이 baseline 에 비해서 줄어드는걸 볼 수 있음
Recap: Batch Normalization
- $\gamma$ : scaling factor, $\beta$ : shift factor, $\mu, \sigma$ : mean, var over a batch(computed for each batch)


- Inference time(testing time)에는 전체 train dataset 의 mean, var 를 저장해놓고 사용; freezed BN
(실 구현에서는 효율을 위하여 지수 이동 평균(EMA)등의 기법을 적용하여 구현) - Normalize 또한 affine mapping 이므로, 두 affine mapping 을 하나의 affine mapping 으로 묶어 사용(아래, 11)

Recap: Freezed Batchnorm as 1x1 Conv
- Feature map $F$ 의 크기를 $C \times H \times W$ (out channel, height, width)라 하고, $F_c$ 는 특정 out channel $c$ 의 Feature map matrix, 각 out channel $c$ 에서 test time 에서의 batch norm 의 전체 affine mapping (normalize - renormalize)의 scale, shift 를 각각 $\gamma_c, \beta_c$ 라 할 때, 특정한 채널의 각 spatial 한 위치 $i, j$ 에 대한 feature map input $F_{c, i, j}$, Batchnorm 연산의 output $hat{F}_{c,i,j}$ 은 아래와 같이 표현이 가능
- Channel wise 한 연산(채널 내부의 전체 위치에 동일한 연산)이므로, 1x1 Conv 로 표현이 가능

testing time 에서의 BatchNorm 같은 경우는 1x1 Conv 로 표현이 가능한걸 유도해낼 수 있음
Fusing original Conv, BN(1x1) Conv
Freezed Batchnorm 과 Original Conv 를 fusion 한다는 건 Original Conv 와 1x1 Conv 를 fusion 한다는 것과 같은 얘기
Vector unwrapping 부연설명
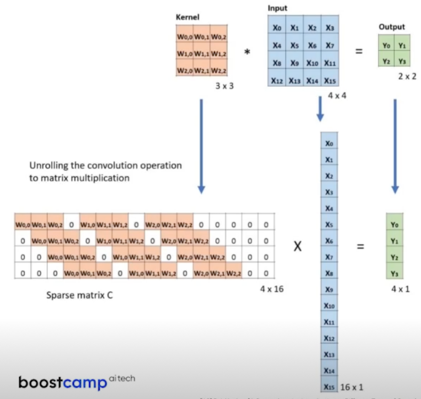
- 실제 Conv 연산의 경우 unrolling 을 통해서 matrix multiplication 을 수행한다.
- 이 과정에서 Input 을 좌측과 같이 vector 로 unwrapping 하여 계산하게 됨
Fusing original Conv, BN(1x1) Conv
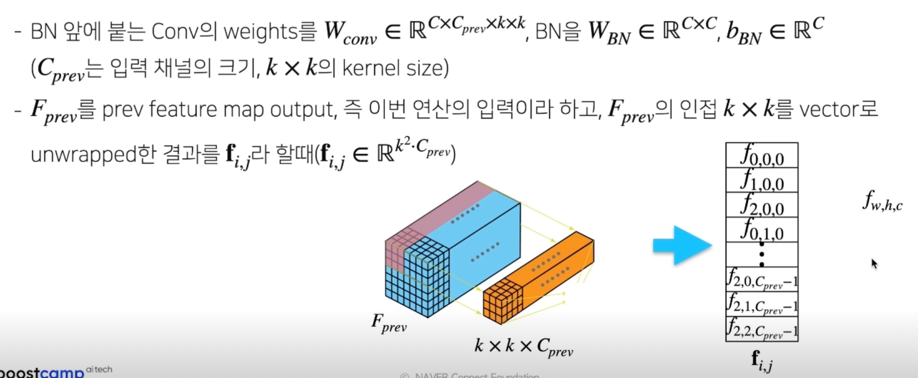
- BN 앞에 붙는 Conv 의 weights 를 $W_{conv} \in \mathbb{R}^{C \times C_{prev} \times k \times k}$,
BN 을 $W_{BN} \in \mathbb{R}^{C \times C}, b_{BN} \in \mathbb{R}^C$
($C_{prev}$ 는 입력 채널의 크기, $k \times k$ 의 kernel size) - $F_{prev}$ 를 feature map output, 즉 이번 연산의 입력이라 하고, $F_{prev}$ 의 인접 $k \times k$ 를 vector 로 unwarpped 한 결과를 $f_{i,j}$ 라 할 때 ($f_{i,j} \in \mathbb{R}^{k^2 \cdot C_{prev}}$)
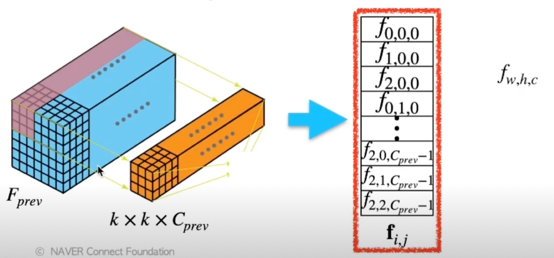
- Batch Normalization 과 Conv layer 의 연산을 다음과 같이 표현할 수 있다

Fusing BN(1x1) Conv, original Conv; code
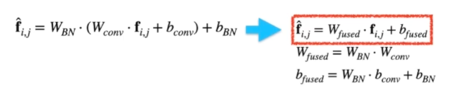

Fusing BN(1x1) Conv, original Conv; simple experiment
- https://colab.research.google.com/drive/1aVtjAMGQoVoGQVCpNnvN2qfC2bZ4zRiQ?usp=sharing
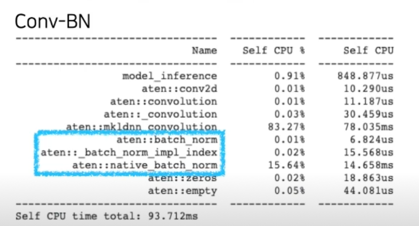
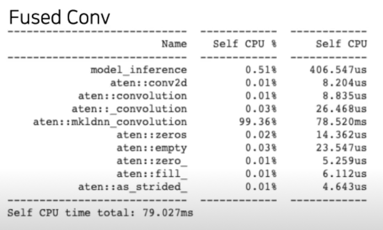
- Resnet18 의 첫번째 레이어만 띄어 Conv-BN 과 Fused-Conv 의 profiler 결과 비교(10개항만 출력)
- CPU 로 inference 를 비교(GPU 는 큰 메모리와 빠른 속도로 차이가 미미 // 전체 모델에 대해서는 유효 예상)
- 속도의 편차가 심하므로, 약간 빨라졌다는 경향성만 파악할 것
2.6 Quantized Layer Fusion(Conv-Activation(ReLU))
Conv-Activation fusion 의 필요성
- Layer fusion 없이는, 각 layer 마다 quantized params($s, z$)가 필요함
- Conv 와 Activation 이 fuse 된다면, scale 을 바꾸기 위해 필요한 DeQuant - Quant 과정이 줄어들게 됨

Matrix multiplication - ReLU Fusion
- Conv 대신 Linear(Matrix multiplication)와 ReLU layer 의 fusion 을 유도
Matrix multiplication(중간) output: $Y_{i,j}$, Activation(최종) output: $Y^’_{i,j}$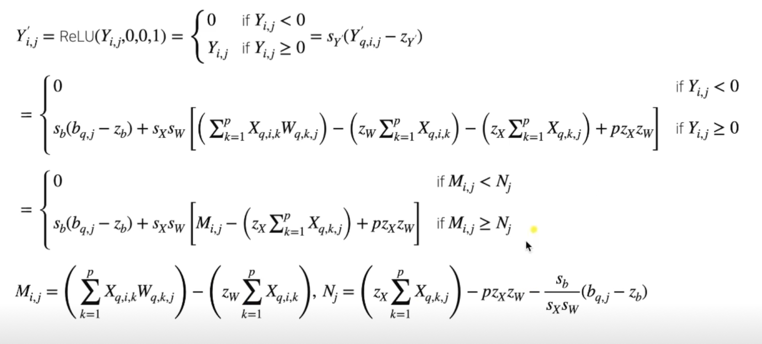
Matrix multiplication - ReLU Fusion; 정리
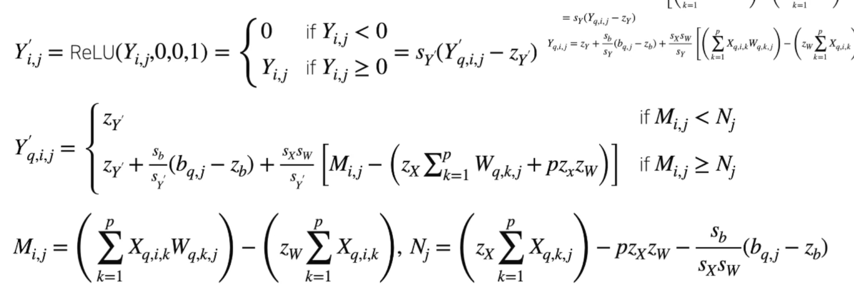

결국은 중간과정인 Quantization, De-Quantization 과정을 생략할 수 있겠다라는 결론을 유도할 수 있음
2.7 정리
이번 강의에서 다룬 것
- Quantization 의 이점
- (Affine) quantization mapping
- Layer 마다 quantization 적용해보기
- Matrix multiplication(Conv layer 연산 또한 동일하게 적용 가능)
- Activation(ReLU)
- Layer Fusion
- Conv-BN $\rightarrow$ Conv
- Fused Quantization(Conv-ReLU quantization 을 한번에!)

댓글남기기