Day_80 01. 모델 경량화 기법 101 - NLP Part 2
작성일
모델 경량화 기법 101 - NLP Part 2
2.3 Knowledge Distillation
Overview
- 가장 핫한 연구 방향(⭐️)
- In which output of teacher will we going to use?
- How will we going to reduce the network?
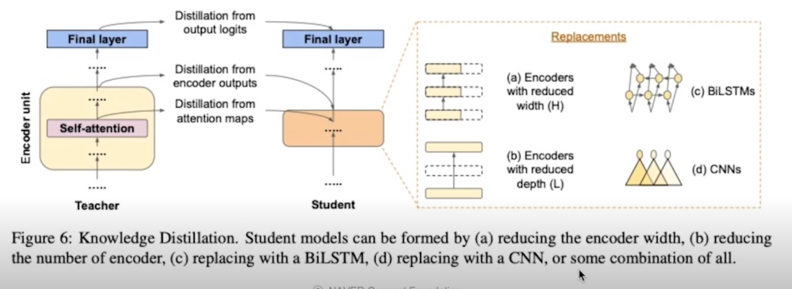
DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter

Overview
- Leverage KD during the pre-training phase
- Linear combination of masked language modeling, distillation(Hinton), cosine-similarity loss
- Result in reducing size of model by 40%, being 60% faster while retaining 97% of its language understanding capabilities(BLUE)
Triple loss = MLM($L_{mlm}$) + Hinton($L_{ce}$) + Cosine embedding($L_{cos}$)
- Masked Language Modeling Loss(CE-loss)
- Distillation(Hinton) Loss(KL div of teacher, student softmax prob with temperature)
- Cosine embedding loss(between teacher, student hidden state vectors)
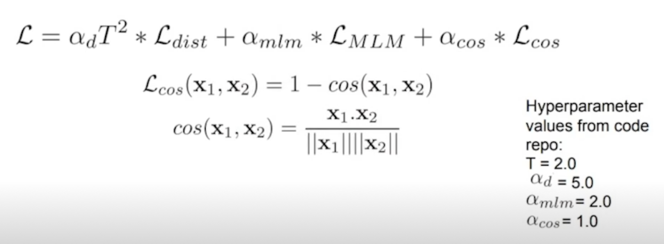
Hiton loss recap
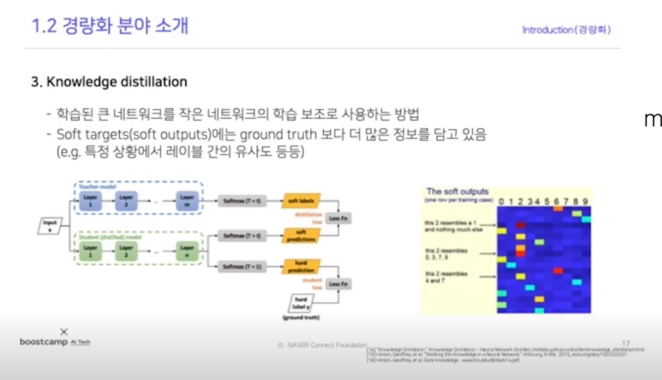
“Some of these ‘near-zero’ probabilities reflects the generalization capabilities of the momdel and how well it will perform on the test set”

하나의 정답으로 학습을 하는것 보다 이런 여러개가 될 수 있다는 가능성과 어떠한 그런 distribution 을 학습하는게 더 효과적이다 라는게 일종의 Hiton loss 에서 얘기하는것과 NLP 에서의 해석이라고 봐야할 것 같음
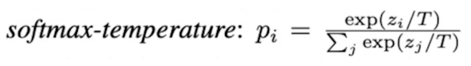
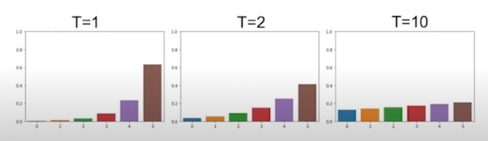
T 가 1일땐 softmax 와 동일
T 가 커질수록 순서는 같은데 Flatten 되는 현상을 볼 수 있음. Smmothing 된다고 볼 수 있음
Student architecture & initialization(paper)

Student architecture & initialization(code(1))
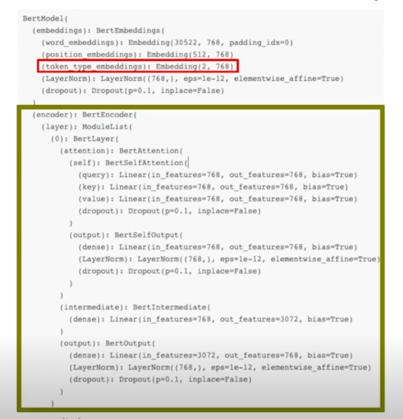
- Token type embedding 제거, pooler 제거
- Transformer 구조는 유지(encoder 갯수 절반)

Student architecture & initialization(code(2))


Experiment(1); evaluation
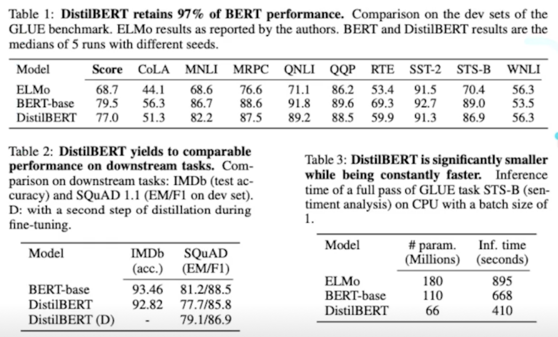
Experiment(2); ablation study

CrossEntropy 가 가장 큰 영향을주고 그 다음은 Cosine 그 다음은 mlm 이었다
initialization 도 굉장히 중요
Experiment(3); notes on inference time, on device computation

TinyBERT: Distilling BERT for Natural Language Understanding

Overview
- Propose
- Transformer distillation method
- Two stage learning framework
- With 4 layers, TinyBERT achieves 96.8% the performance of the teacher(BERT base) on GLUE
- While 7.5x smaller, 9.5x faster on inference.
- TinyBERT with 6 layers performs on-par with its teacher(BERT base)
- 6개의 layer 를 쓰면 BERT base 와 동등한 성능이 나옴
Transformer distillation method; 3 types of loss
- From the output embedding layer
- From the hidden states and attention matrices
- From the logits output by the prediction layer
- Hinton Loss
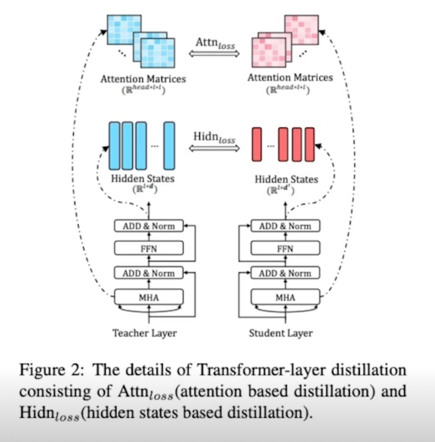
- Teacher has N layers, student has M layers
- Start from choosing M out of N layers
- Define function n = g(m) as the mapping function between indices from student layers to teacher layers
- m-th layer of student model learns the information from the g(m)-th layer of the teacher model (paper used g(m) = 3 * m)

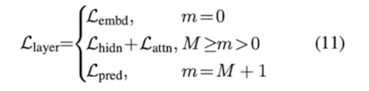
1) Transformer-layer Distillation(Attention based)
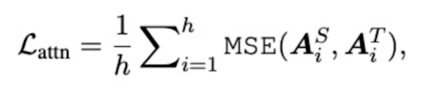
- $A_i \in \mathbb{R}^{l \times l}$ : i-th head of teacher or student model’s attention matrix
$l$ : input text length, MSE denotes mean squared error - In this paper, authors set up unnormalized attention matrix $A_i$
(not distribution(softmax output), showed faster convergence, better performance)
1) Transformer-layer Distillation(Hidden state)
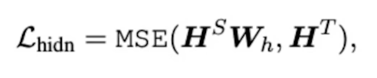
- $H^S \in \mathbb{R}^{l \times d^’}$ : hidden state of student
$H^T \in \mathbb{R}^{l \times d}$ : hidden state of teacher (usually, $d > d^’$)
$W_h \in \mathbb{R}^{d^’ \times d}$ : Learnable linear transformation(maps hidden states of student into the same space as the teacher’s hidden states)
2) Embedding-layer distillation loss
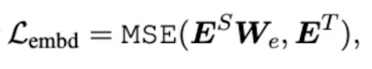
- $E^T, E^S$ : embedding dimension of teacher, student
$W_E$ : works same as $W_h$
(maps student’s embedding states into teacher’s)
3) Prediction-layer Distillation(hinton loss
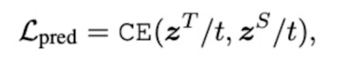
Wramup
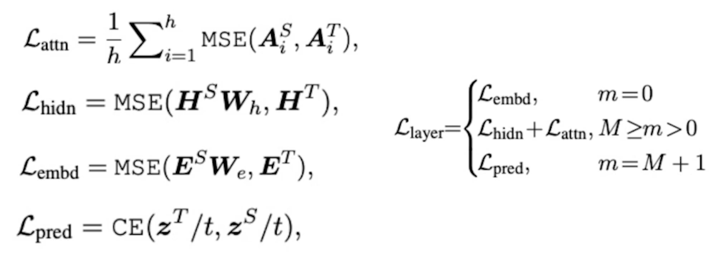
TinyBERT Learning
- Suggests two stage learning framework: general distillation, task-specific distillation (more on paper)
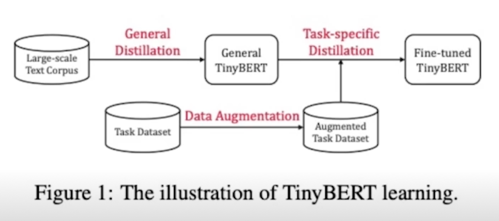
Experiments
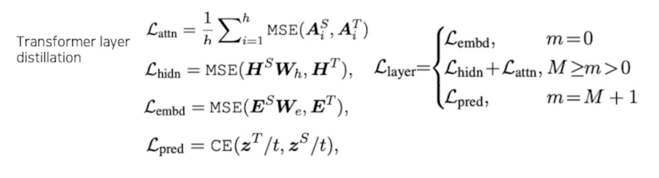
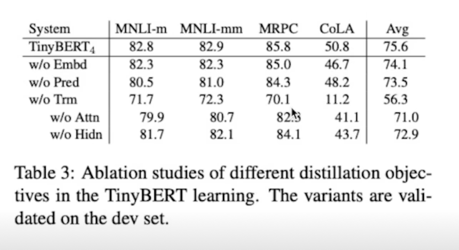
기타 논문 추천(+ 한 줄 summary)
-
MobileBERT: a Compact Task-Agnostic BERT for Resource-Limited Devices
(https://arxiv.org/pdf/2004.02984.pdf)
Inverted Bottleneck 구조 제안, BERT 대비 4.3배 소형화, 5.5배 속도 향상, 모바일에서 62ms 달성
(+ 기타 여러 실험들(layernorm 제거, activation 변경, KD 기법 다르게 적용 등) 매우 다양한 ablation study!)
(+ TFLite 로 바로 사용가능한 모델이 공개) -
Exploring the Boundaries of Low-Resource BERT Distillation
(https://aclanthology.org/2020.sustainlp-1.5.pdf)
Conv 기반, BiLSTM 기반 + KD, 큰 성능드랍 but, 약 570배, 약 40배 속도 향상 -
AdaBERT: Task-Adaptive BERT Compression with Differentiable Neural Architecture Search
(https://arxiv.org/pdf/2001.04246.pdf)
KD + NAS(CNN based)로 sub task 학습, avg -2.0 point 의 성능 드랍 대비 약 20배의 속도 향상
Comments
- Pros: 파라미터 수 감소, 다양한 range 모델(성능 range), 큰 속도 향상 여지(LSTM 등 다른 구조로 Distillation)
Cons: 비교적 복잡한 학습 구성, code maintain
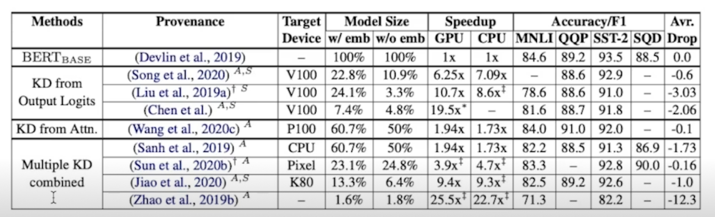
- KD 는 기타 다른 method 와도 접목이 가능
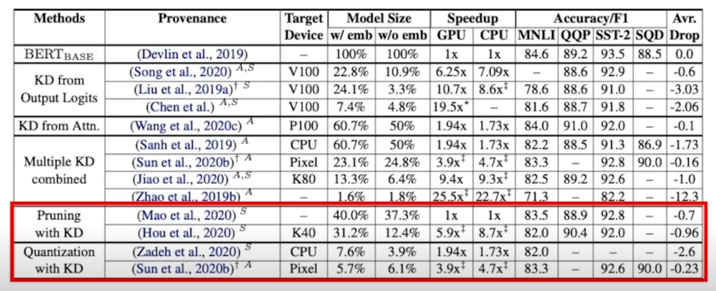
2.4 Quantization
Overview
- Q 의 장점: low memory footpring, inference speed(low precision operation 증가 추세)
- 주로 Quantization 과정에서 발생하는 accuracy drop 을 줄이는 방향에 대한 연구
QAT(Quantization Aware Training), Quantization range 계산 방법 제안 등등
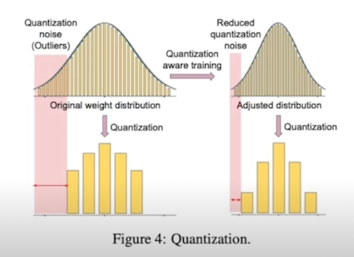
Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT

- Suggests mixed-precision quantization on BERT(using analysis of Hessian information)
// 민감도가 높은 layer 는 큰 precision, 낮은 layer 는 작은 precision - Proposes a new quantization scheme, named group-wise quantization
- Investigates the bottlenecks in BERT
- Achieves 13x compression ratio in weights, 4x smaller activation, 4x smaller embedding size with 2.3% accuracy loss
Hessian spectrum(eigenvalues)
- The params in NN layers with higher Hessian spectrum(larger top eigenvalues) are more sensitive to quantization and require higher Hessian spectrum
- Hessian 의 eigenvector 중 가장 큰 두개의 방향으로 weight param 에 perturbing 을 주었을때, loss 의 변화
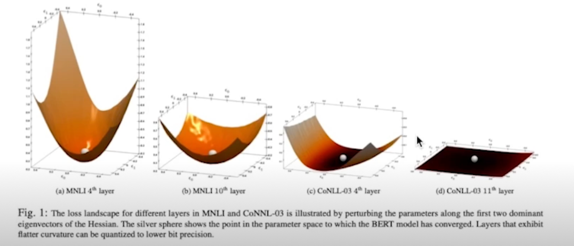
Hessian 의 top eigenvalues 의 크기가 해당 레이어의 민감도와 연관이 있다
논문에서는 아래 문제들의 해결 또한 제안 1) Hessian spectrum 계산의 복잡성 $\rightarrow$ power iteration method(Large sparse mtrix 에서의 빠른 수렴) 2) 같은 데이터셋이더라도 Hessian spectrum 의 var 이 매우 큼 $\rightarrow$ mean, std 를 함께 고려하여 민감도를 정렬
Group-wise Quantization method
- Directly quantizing each 4 matrices(key, query, value, and output) in MHA as an entirely with the same quantization range can significantly degrade the accuracy
- Paper suggests divide quantization range by subgroups, each sub-group have its own quantization range
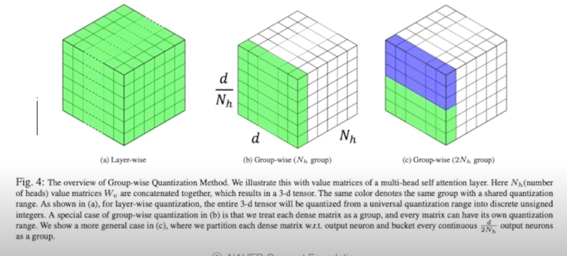
Experiment
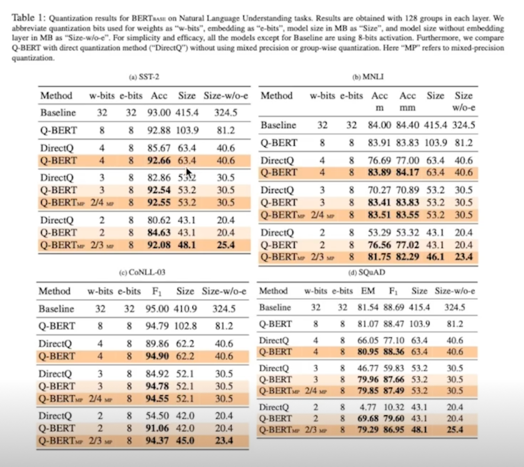
Comments
- Pros: 모델 사이즈 감소 탁월, 적은 성능 하락
Cons: 속도 향상 불투명(속도 향상 지원 증가 추세(e.g., Nvidia tensor-core, XNNPACK))

3. Notes on model compression
3.1 결과 정리
전체 결과
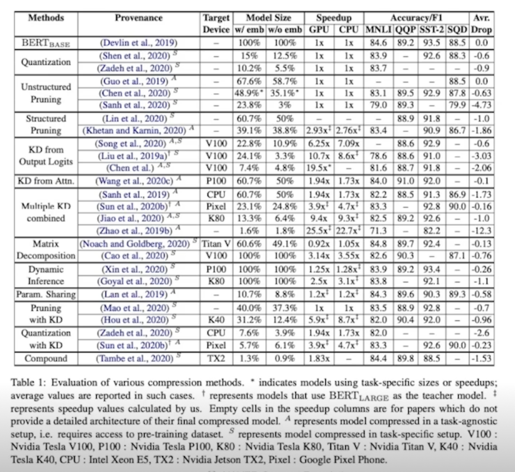
3.2 Wrap up
Conclusion: No Free Lunch Tehorem
- 각 기법 마다 확실한 장단이 존재(물론 보완하는 논문들도 존재)
- 논문에서의 포장에 주의할 것(복잡한 후 처리가 필요하거나, 특정 상황에서만 적용가능하거나, …)
- 주어진 시간이 넉넉하다면 여러 기법을 혼합해서 사용하는 것이 가장 효과적


댓글남기기