Day_75 03. 작은 모델, 좋은 파라미터 찾기: AutoML 이론
작성일
작은 모델, 좋은 파라미터 찾기: AutoML 이론
1. Overview
1.1 Conventional DL Training Pipeline
So called “Data Engineering”
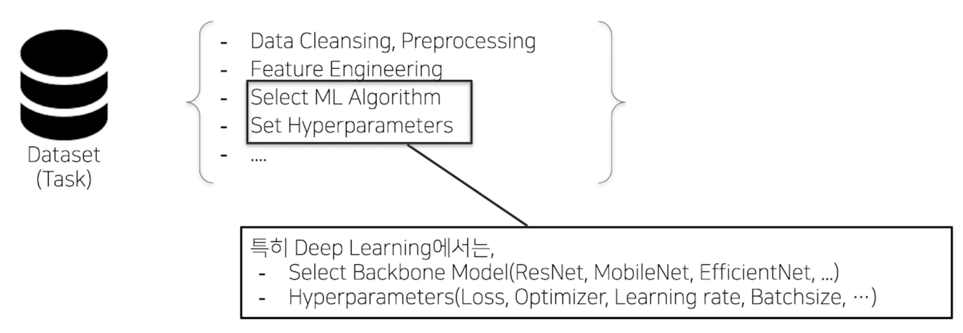

데이터셋이 주어졌을때 성능이 잘나올 것 같은 Model Architecture 를 선정하고 Hyperparameter 를 고름
그 다음엔 학습을 하고 성능이 얼마나 잘나오는지 Evaluateion 함
성능이 어느정도 나오면 Hyperparameter Tuning 을 해보고 성능이 잘 안나오면 Model Architecture 를 바꿔보고 이런식으로 사람이 반복해서 이 과정을 거침
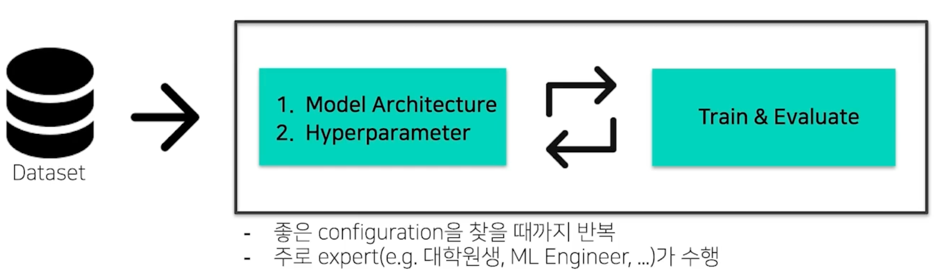
여기서의 가장 큰 문제점은 사람이 이걸 해줘야하는게 큰 문제점이라고 생각함

1.2 Objectives of AutoML
AutoML: “True” End-to-end learning

AutoML(HPO: Hyperparameter Optimization)의 문제 정의

1.3 Properties of configurations in DL
DL model Configuration(Architecture, Hyperparameter)의 특징
- 주요 타입 구분
- Categorical
- ex) optimizer: [Adam, SGD, AdamW, …], module: [Conv, BottleNeck, InvertedResidual, …]
- Continuous
- ex) learning rate, regularizer param, …
- Integer
- ex) batch_size, epochs, …
- Categorical
- Conditional(⭐️): 한 configuration 에 따라 search space 가 달라질 수 있음
- Optimizer 의 sample(e.g. SGD, Adam 등등)에 따라서 optimizer parameter 의 종류, search space 도 달라짐
- (e.g. optimizer 에 따른 learning rate range 차이, SGD: momentum, Adam: alpha, beta1, beta2, … 등등)
- Module 의 sample(e.g. Vanilla Conv, BottleNeck, InvertedResidual 등등)에 따라서 해당 module 의 parameter 의 종료, search space 도 달라짐
- Optimizer 의 sample(e.g. SGD, Adam 등등)에 따라서 optimizer parameter 의 종류, search space 도 달라짐
1.4 모델경량화 관점에서의 AutoML
(주어진)모델을 경량화하자 vs (새로운)경량 모델을 찾자
모델경량화의 접근 두가지
- 기존 가지고 있는 모델을 경량화 하는 기법
- Pruning, Tensor decomposition, …
- Search 를 통하여 경량 모델을 찾는 기법
- NAS(Neural Architecture Search), AutoML(Automated Machine Learning), …
이 강의에서는 Search 를 통하여 경량 모델을 찾는 기법 을 주로 다룰 예정
2. Basic Concept
2.1 AutoML Pipeline
일반적인 AutoML Pipeline
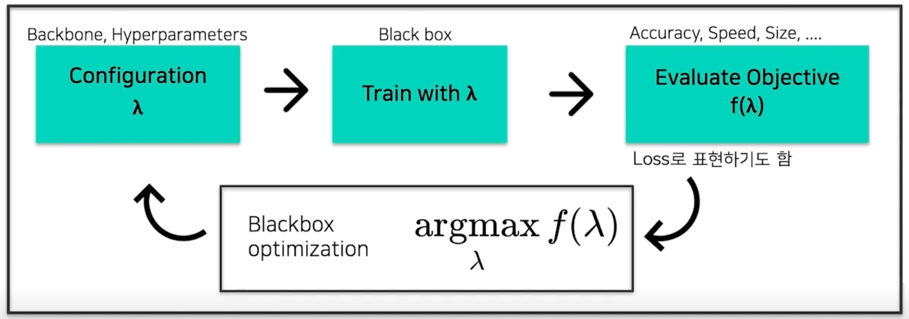
어떤 Configuration $\lambda$(흔히 말하는 Backbone, Hyperparameter 를 모두 포함하는 concept) 를 정하게되고 이 configuration 으로 모델 학습을 할 수 있음
이 모델에 대해서 학습된 모델이 얼마나 잘되느냐는 blackbox 임 즉, 알 수 없음
이 학습된 모델을 가지고 Task 마다 다른데 얻고자 하는 목적함수($f(\lambda)$를 모델링함
Task 마다 다르다는 말은 속도는 상관없이 성능만 좋았으면 좋겠어 라는 요청이 있을수도 있고 아니면 성능도 좋고 속도도 어느정도 빨랐으면 좋겠어 또는
성능은 적당하되 사이즈는 작았으면 좋겠어 라는 상황에 맞는 요청, 목적들이 있음
이거에 따라서 $f$ 를 적절하게 설정해서 모델을 평가함
Blackbox optimization 이 부분이 AutoML 이 주로 하게되는 역할임
이 $f(\lambda)$ 를 maximize 하는게 AutoML 의 역할임
우리가 평가한 Objective 값을 가지고 그 다음에 어떤 $\lambda$ 를 찾아보면 좋을까를 정해주는게 AutoML 의 하는 역할임
이걸 반복적으로 수행하다보면 결국 우리가 원하는 좋은 objective 값을 가지는 모델을 찾을 수 있지 않겠어? 라는 흐름으로 보면됨
AutoML Pipeline 예시: Bayesian Optimization(BO)
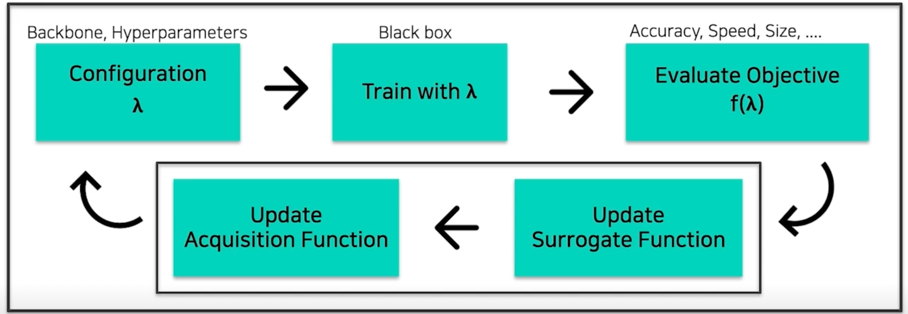
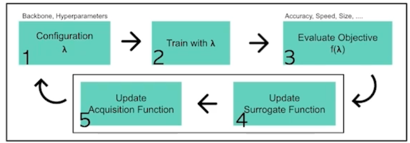
일반적으로 blackbox optimization 이라고 했던 부분은 두 가지 과정을 거침
첫번째는 Surrogate Function 이르는걸 업데이트하고 Acqueisition Function 을 업데이트해서 다음 시도할 configuration 을 정하고 이 일련의 과정을 계속해서 반복하는 구조를 이룸
Surrogate Function 은 objective $f(\lambda)$ 를 예측하는 regression model 임
이걸 예측할 수 있게되면 다음 $\lambda$ 를 어디를 찾아보면 좋을까를 판단할 수 있게됨
Acquistion Function 은 Surrogate Function 을 가지고 다음 시도해 볼 $\lambda$ 를 결정하는 거라고 보면 됨
2.2 Bayesian Opimization(with Gaussian Process Regression)
Bayesian Optimization
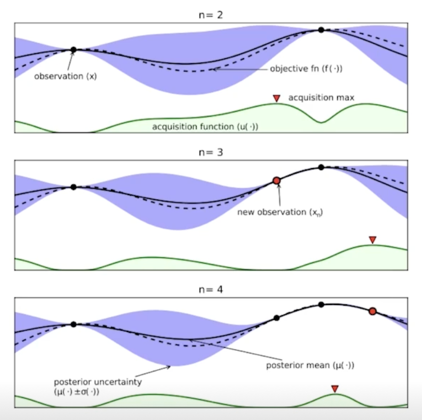
매 iteration 마다,
- $\lambda$(그림의 x)를 sample(observation)
- 해당 sample(configuration)로 DL 모델을 학습
- objective 를 계산(우측 point)
- Surrogate model 업데이트(그림의 실선, 파란 영역)
- (ex: GP model, posterior mean, posterior variance(uncertainty))
- Acquisition function 업데이트(그림의 초록 영역)
- Expected Improvement, Upper Confidence Bounds
(엄밀하지 않은) 간단 설명: Gaussian Process Regression(Function space view)
- 일반적인 Regression task: “Estimate the function f fits the data the most closely”
- Set of train data: ($X$, $Y$), Set of test data: ($X_* , Y_* $), $Y \approx f(X) + e$)
- 우리가 알고자 하는 특정 위치의 $Y_*$ 값은 우리가 알고 있는 $X, Y, X_*$ 들과(positive 건, negative 건) 연관이 있지 않을까?
- $\rightarrow$ $X, Y, X_*$ 값으로 부터 $Y_*$ 를 추정, 연관에 대한 표현은 Kernel 함수 $K$ 로!
- f(x) 를 “Possible output of the function f at input x” 인 “Random variable” 로 보고, 각 r.v. 들이 Multivariate
Gaussian distribution 관계에 있다고 가정
- = 함수들의 분포를 정의하고, 이 분포가 Multivariate Gaussian distribution 을 따른다 가정
- = 함수 f 가 Gaussian process 를 따른다
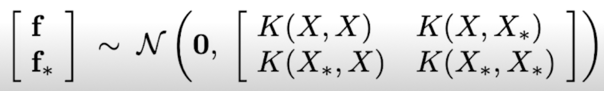
-
알고자 하는 값(test) $f_* \approx Y_*$ 와 아는 값(train) $f \approx Y$ 의 관계를 정의
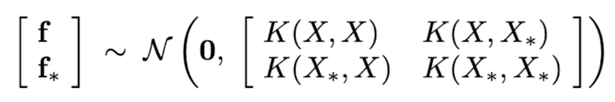
-
+Gaussian Identities(Gaussian 의 marginal, conditional 도 Gaussian)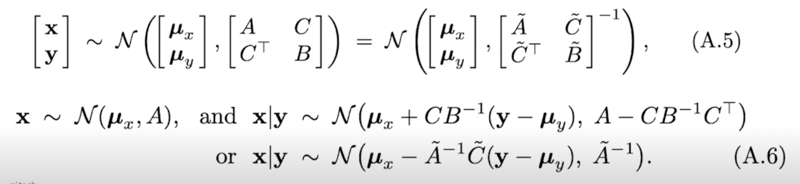
Gaussian Identities 그림 보충
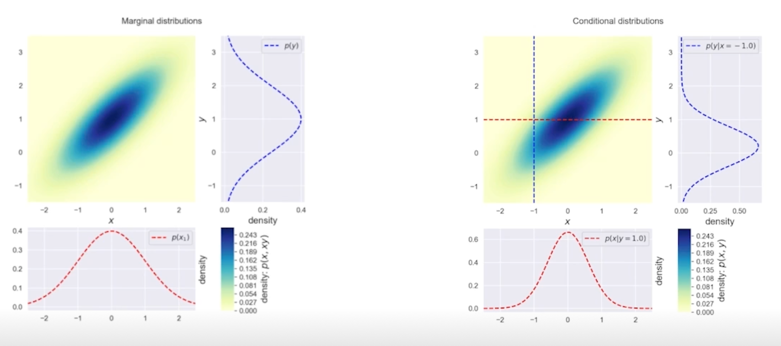
2개의 변수를 가지는 Gaussian 변수가 있을 때, 아래에서 위로 바라보는 marginal 분포도 Gaussian 이고 오른쪽에서 왼쪽으로 보는 marginal 분보도 Gaussian 이다
이게 실제로 Gaussian 이다라는걸 증명하는건 아니지만 concept 을 잡을 수 있겠다고 생각해서 가져왔음
오른쪽 그림에서는 어느 위치에서 자르더라도 실제로 다 Gaussian 을 이룬다
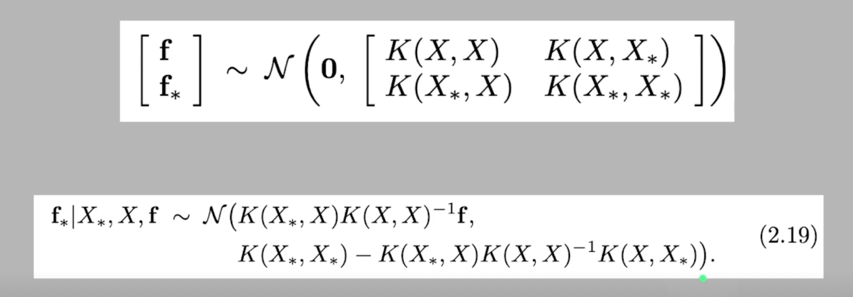
함수들의 분포를 위처럼 정의했었고 거기에 더해서 Gaussian Identities 를 정의를 하면
알고 있는 $X, Y$ 데이터 pair 랑 알고자하는 위치값인 $X_$ 를 알고있으면 $f_$ 에 대한 분포를 알 수 있는것임
분포라는건 평균($K(X_, X)K(X, X)^-1f$)과 분산($K(X_, X_) - K(X_, X)K(X, X)^-1K(X, X_*)$) 값으로 표현할 수 있음
추천 페이지
https://distill.pub/2019/visual-exploration-gaussian-processes
Surrogate Model(Function): $f(\lambda)$ 의 Regression model
- Objective $f(\lambda)$ 값을 예측하는 모델
- (지금까지 관측된 $f(\lambda)$ 들이 있을 때, 새로운 $\lambda^$ 에 대한 objective($f(\lambda^)$ 는 얼마일까?)
- Objective 를 estimate 하는 surrogate model 을 학습, 다음 좋은 $\lambda$ 를 선택하는 기준으로 사용
-
대표적인 Surrogate model 로는 Gaussian Process Regression(GPR) Model (Mean: 예측 $f$ 값, Var: uncertainty)
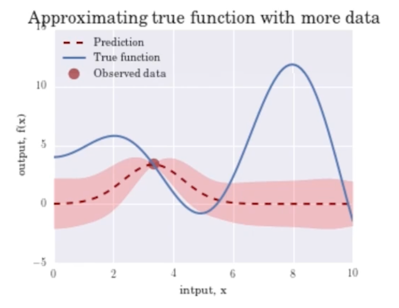
데이터 포인트가 하나일 때 Gaussian Process 의 예측결과는 Mean 은 실제값은 파란 실선일 때, 빨간색 점선으로 예측될거고 불확실성은 핑크영역으로 넓음
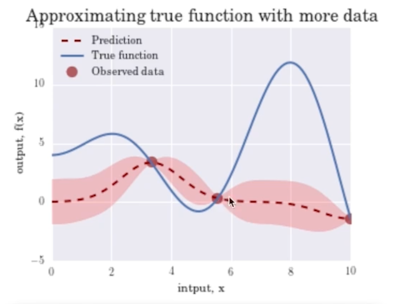
포인트가 좀 더 생기면 포인트가 생긴지점에서는 불확실성이 없음 실제로 관측을 했으니까
대신 관측한 포인트들 사이에 대해서는 아직 못봤으니까 불확실성이 있음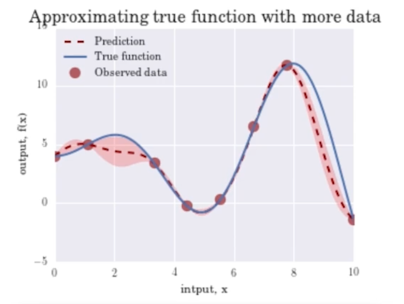
점점 관측이 늘어날수록 함수가 fitting 이 되면서 더해져서 Variance 값도 줄어드는걸 확인할 수 있음
Acquisition Function: 다음은 어디를 trial 하면 좋을까?
-
Surrogate model 의 output 으로부터, 다음 시도해보면 좋을 $\lambda$ 를 계산하는 함수
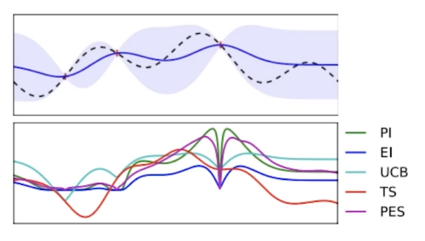
- Exploration vs Exploitation (“불확실한 지점 vs 알고있는 가장 좋은 곳” 의 trade off)
- Acquisition function 의 max 지점을 다음 iteration 에서 trial
-
Ex) Upper Confidence Bound(UCB)
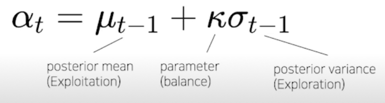
mean 값인 $\mu_{t-1}$ 은 Exploitation 으로 아는 값중에 가장 좋은지점이고 높으면 좋음
variance 값인 $\sigma_{t-1}$ 은 불확실성으로 높으면 높을수록 좋음
Tree-structured Parzen Estimator(TPE)[6]
- GP 의 약점:
- High-dim(O(N**3))
- Conditional(⭐️), cont/disc 파라미터들의 혼재시 적용이 어려움
- 이 부분이 문제가 많아서 TPE 를 많이 사용하는 것 같음
-
TPE: GPR($p(f \lambda)$)과 다르게 $p(\lambda f)$ 와 $p(\lambda)$ 를 계산 - TPE 를 통한 다음 step 의 $\lambda$ 계산 방법
- 현재까지의 observation 들을 특정 quantile(inverse CDF)로 구분
- (ex, 전체 중 75% bad, 25% good)
- KDE(Kernel density estimation)으로 good observations 분포(p(g)), bad ovservations 의 분포(p(b))를 각각 추정
- (greater 의 분포, lower 의 분포)
- p(g)/p(b) 은 EI(Expected Improvement, acquisition function 중 하나)에 비례하므로([6]), 높은 값을 가지는 $\lambda$ 를 다음 step 으로 설정
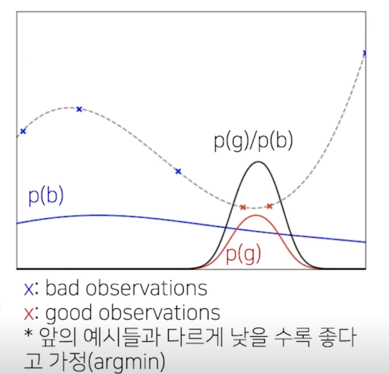
- 현재까지의 observation 들을 특정 quantile(inverse CDF)로 구분
Tree-structured Parzen Estimator(TPE): EI 증명
-
Likilihood 를 Quantile 로 구분되는 두 함수로 정의

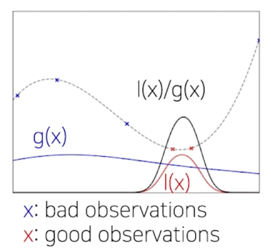
결론은 l(x)/g(x) 에 비례한다는 식이 됨
직관적으로 보자면, l(x)(좋았던 관측 분포), g(x)(안좋았던 관측 분포) l(x)/g(x)가 가장 높은 지점을 탐색한다?
l(x)가 높은 쪽을 선호하되, g(x)가 낮은 곳도, 즉, 안좋은지 알 수 없는 곳도 찾아보자는 의미
3. Further Studies
3.1 한계점 및 연구 키워드
가장 큰 문제는
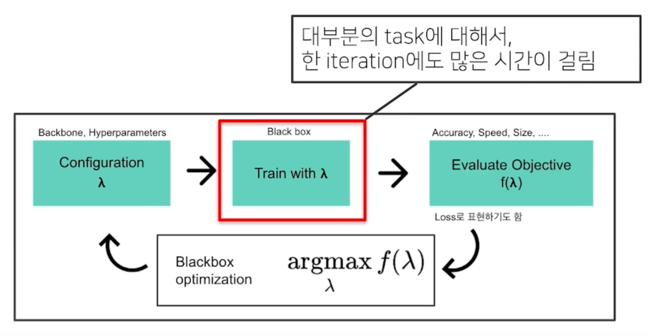
일반적으로 100~200번을 돌려야하는데 resource 도 문제고 시간도 문제
아직은 활발한 연구분야
- DL 에서의 AutoML 은 scalability 이슈가 더욱 대두됨
- 주요 키워드
- Hyperparameter Gradient Descent(탐색과 학습을 동시에)
- Meta-learning(Auto “AutoML”)
- Multi-=fidelity optimization
- Data 의 subset 만을 활용
- 적은 epoch
- RL 을 활용한 적은 trial
- Image Downsampling 등등
3.2 현실적인 접근
절충안: 그럼에도 불구하고
충분히 절충 가능(Where engineering comes in)
- 어느 정도의 prior 를 개입, 적은 search space 를 잡고,
- 적지만, 대표성을 띄는 좋은 subset 데이터를 정하고(+ n-fold Cross validation 등의 테크닉)
- 학습 과정의 profile 을 보고 early terminate 하는 기법 적용
- ASHA, Scheduler, BOHB(Bayesian Optimization & hyperband)
등등의 방법으로 Human in the loop 의 결과보다 “충분히 좋은” configuration 을 찾을 수 있습니다.

댓글남기기