Day_48 02. Scaling up with FAISS
작성일
Scaling up with FAISS
1. Passage Retrieval and Similarity Search
복습 : Retrieval with dense embedding
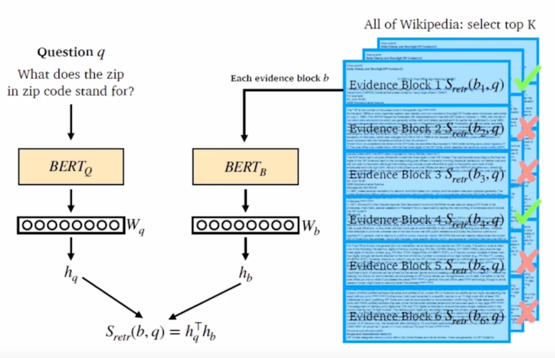
question 쪽은 질문이 들어올때마다 encoding 을 해줘야 하는 부분이고 passage 쪽은 미리 passage 를 확보한 상태라면 offline 으로 전부 다 연사을 하고나서 저장을 해놨다가 새로운 지문이 들어올때마다 기본 passage 들과 비교해서 가장 유사도가 높은 passage 를 내보내는 방식을 취함
인퍼런스 : Passage 와 query 를 각각 임베딩한 후 query 로 부터 거리가 가까운 순서대로 passage 에 순위를 매김
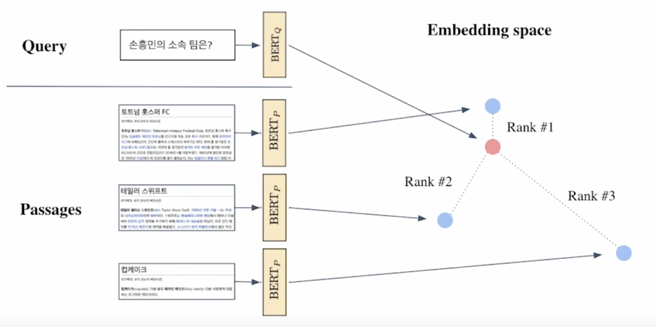
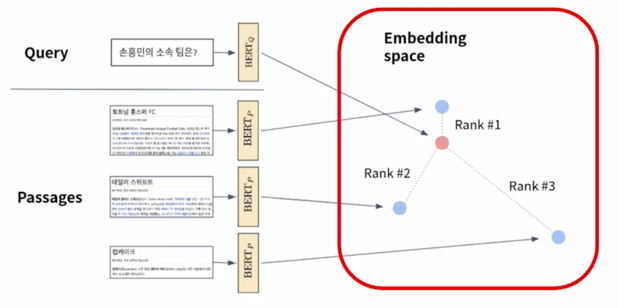
HOW to find the passage in real time? $\rightarrow$ Similarity Search!
passage 가 늘어날 수록 파란 점들이 엄청 많아지게 되는데 기본적인 score 를 계산하는 방식은 질문과 각각의 passage embedding 을 dot-product 하는 것이고 dot-product 조차도 dimension 이 커지면 꽤나 부담스런 연산이 될 수 있는데 파란색점이 정말 많아지게 되면 어떻게 효율적으로 가장 가까운 문서를 혹은 가장 가까운 벡터를 찾을 수 있을까가 오늘 주제에 가장 중요한 골자임
그리고 이 과정을 일반적으로 Similarity Search 라고 부르는데 말 그대로 검색을 상당히 빠르게 하는 것임
MIPS(Maximum Inner Product Search)
주어진 질문(query) 벡터 q 에 대해 Passage 벡터 v 들 중 가장 질문과 관련된 벡터를 찾아야함
- 여기서 관련성은 내적(inner product)이 가장 큰 것
기본적으로는 이쪽 분야에서는 inner product 가 많이 쓰이고 있음
가장가까운 벡터를 찾겠다라고 하면 Maximum Inner Product 를 찾겠구나라고 생각하면 좋음
다만 개념적으로는 좀 더 L2 같은 유클리디언 스페이스에서의 거리를 생각하시는게 개념 정리하시거나 상상을 하는데는 조금 더 도움이 됨

4, 5강에서 사용한 검색 방법: brute-force(exhaustive) search
- 저장해둔 모든 Sparse/Dense 임베딩에 대해 일일히 내적값을 계산해서 가장 값이 큰 passage 를 추출
개수가 많아지면 많아질수록 비효율적임
MIPS in Passage Retrieval
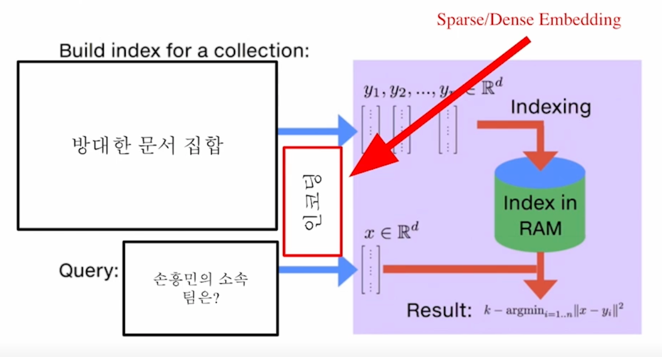
방대한 문서 집합의 vector 들을 저장해놓은 다음에 저장된 값들을 real time 으로 query 가 들어올 때마다 해당되는 vector 를 찾아주는 방식임
지금까지 vector 로 변환해주는 encoding 방법론을 봤다면 오늘은 encoding 을 하고 난 다음에 검색하는 과정을 조금 더 smart 하게 효율적으로 할 수 있을지를 보자
MIPS & Challenges
실제로 검색해야할 데이터는 훨씬 방대함
- 5백만 개(위키피디아)
- 수십 억, 조 단위까지 커질 수 있음
- $\rightarrow$ 따라서 더이상 모든 문서 임베딩을 일일히 보면서 검색할 수 없음

검색해야할 데이터는 너무 많은데 유저가 검색할 때 답변이 오기까지의 time limit 은 굉장히 짧음
예를들어 검색엔진에 질문을 던졌는데 그거에대한 답이 내일 또는 일주일 후에 나온다면 상당히 불편함
따라서 이런 방대한 문서를 짧은 시간내에 훑으면서 가장 가까운 문서 가장 가까운 벡터를 찾는 알고리즘이 상당히 중요함
Tradeoffs of similarity search
1) Search Speed
- 쿼리 당 유사한 벡터를 k 개 찾는데 얼마나 걸리는지?
- $\rightarrow$ 가지고 있는 벡터량이 클 수록 더 오래 걸림 2) Memory Usage
- 벡터를 사용할 때, 어디에서 가져올 것인지?
- $\rightarrow$ RAM 에 모두 올려둘 수 있으면 빠르지만, 많은 RAM 용량을 요구함
- $\rightarrow$ 디스크에서 계속 불러와야한다면 속도가 ㄴ려짐 3) Accuracy
- brute-force 검색 결과와 얼마나 비슷한지?
- $\rightarrow$ 속도를 증가시키려면 정확도를 희생해야하는 경우가 많음
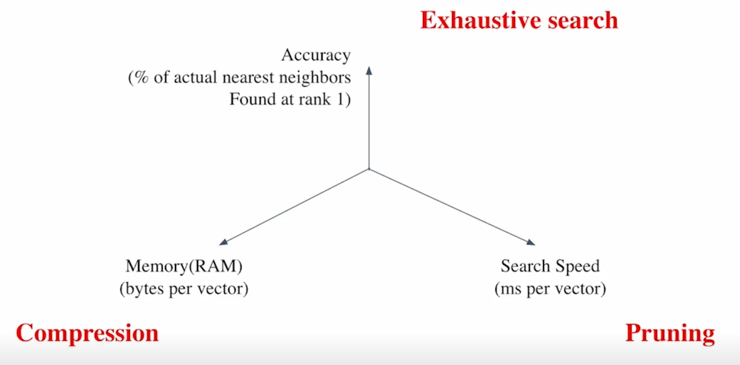
기본적으로는 이 3가지 문제를 접근하는 방법론이 각각 하나씩 있음
결국에는 accuracy 를 올리는 부분에서는 어떻게하면 검색을 더 효율적으로 할 것인가에 대해서 고민을 해야하고 memory 같은 경우는 줄이기 위해서 Compression 을 고민해야하고 어떻게 더 적은 용량으로 저장할 수 있을것인가 마지막으로는 Search Speed 를 더 올리기 위해서는 inference time 때 pruning 같은 mechanism 을 활용해서 approximation 을 더 많이 하는 대신 경우에 따라서는 정확성을 좀 잃더라도 필요한 속도를 확보하는것이 중요하다고 할 수 있음
Tradeoff of search speed and accuracy
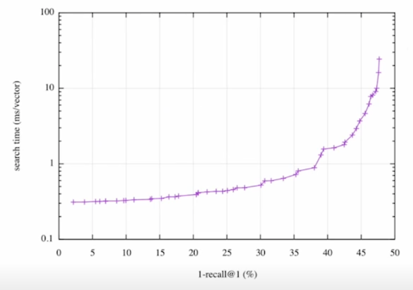
속도(search time)와 재현율(recall)의 관계
- 더 정확한 검색을 하려면 더 오랜 시간이 소모됨
Increasing search space by bigger corpus
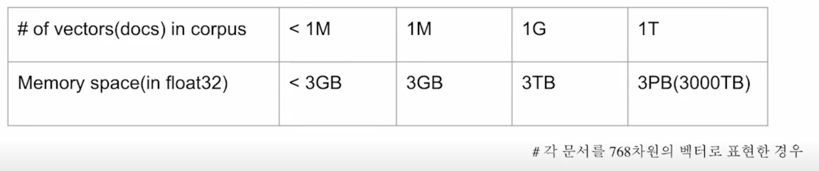
코퍼스(corpus)의 크기가 커질 수록
- 탐색 공간이 커지고 검색이 어려워짐
- 저장해 둘 Memory space 또한 많이 요구됨
- Sparse Embedding 의 경우 이러한 문제가 훨씬 심함
- 예) 1M docs, 500K distinct terms = 2TB
2. Approximation Similarity Search
Compression - Scalar Quantization (SQ)
Compression : vector 를 압축하여, 하나의 vector 가 작은 용량을 차지 $\rightarrow$ 압축량 up $\rightarrow$ 메모리 down, 정보 손실 up
ex) Scalar quantization : 4-byte floating point $\rightarrow$ 1-byte (8bit) unsigned integer 로 압축
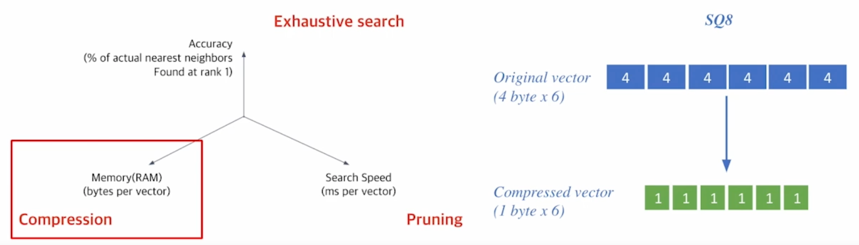
숫자를 compression 하는 방법론
보통 어떤 숫자를 저장할때는 float32 라는 4-byte 체계를 활용함
하지만 실제 inner-product search 를 할때는 4-byte 까지 필요한 경우는 많지 않음
1-byte 로 어느정도 approximate 한 다음에 저장하더라도 상당히 정확한 경우가 많음
이런 프로세스를 Scalar quantization 이라고 부르는데 말 그대로 각각 수치를 Qunatize 를 해가지고 Quantize 를 한 값에서 용량을 줄일 수 있도록 해줌
기본적으로 float32 에서 4배로 압축할 수 있음
Pruning - Inverted File (IVF)
Pruning : Search space 를 줄여 search 속도 개선 (dataset 의 subset 만 방문)
$\rightarrow$ Clustering + Invented file 을 활용한 search
1) Clustering : 전체 vector space 를 k 개의 cluster 로 나눔 (ex. k-means clustering)
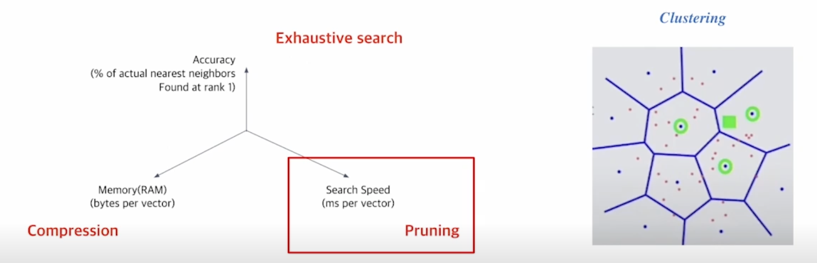
간단히 말하자면 pruning 이라고 하면 점들을 정해진 cluster 로 소속을 시켜서 군집을 일으키는 형태를 말함
이렇게 군집이 이뤄진 상태에서 query 가 들어왔을때 query 가 모든 군집(cluster)을 다 visit 하는 것이 아니라 그림의 오른쪽에서 4각형이 query 인데 가장 근접한 cluster 만 보는 방식을 택함
실제로 clustering 이 잘 되어있다고 한다면 멀리있는 cluster 을 볼 필요가 없음
결국은 가장 근접한 cluster 만 방문함으로써 여기서는 3개의 cluster 가 될 것이고 3개의 군집내에 있는 point 들에 대해서는 exhaustive search 로 다 직접 비교함
예를 들어 데이터포인트가 100만개인데 cluster 가 1000개라고 한다면 그리고 각 query type 마다 10개의 cluster 만 visit 한다고 하면 원래는 1000개 전부 다 cluster 를 visit 해서 100만개의 point 를 봐야한다고 했을 때 100분의 1인 10개만 보고 실제 속도같은 경우도 100분의 1로 줄일 수 있음
clustering 으로 가장 많이 활용되는 방법론은 k-means clustering 임
k-means clustering 을 통해서 cluster 를 먼저 정의하고 그 다음에 각 document vector 들의 cluster 와 가장 가까운 cluster 에 속하게 한 다음에 군집이 형성되면 가장 가까운 cluster 만 순차적으로 방문함으로써 속도를 비약적으로 늘릴 수 있음
- 2) Inverted file (IVF)
- Vector 의 index = inverted list structure
$\rightarrow$ (각 cluster 의 centroid id)와 (해당 cluster 의 vector 들)이 연결되어있는 형태
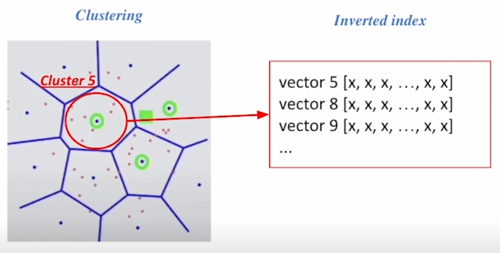
이런 방법론을 Inverted file 이라고 부르는 이유도 실제 각 cluster 에 속해있는 point 들을 역으로 index 로 가지고 있기 때문임
이것을 inverted list structure 라고 부르고 각 cluster 의 centroid id 와 해당 cluster 들의 vector 들이 연결되어있는 형태라고 보면 됨
특정 vector 5 에 어떤 것들이 연결되어있는지를 쫙 list 가 되어있음
각각 vector 마다 연결되어 있는 centroid 들이 list 되는 방식으로 data 구조가 변경됨
이렇게되면 cluster 를 찾은 다음에 cluster 에 속해있는 vector 들을 빠르게 확보가 가능함으로써 실제로 search space 를 비약적으로 빠른 시간내에 줄일 수 있음
Introduction to FAISS
What is FAISS
FAISS github : https://github.com/facebookresearch/faiss
FAISS tutorial : https://github.com/facebookresesarch/faiss/tree/master/tutorial/python

FAISS 는 facebook 에서 만든 fast approximation 을 위한 라이브러리임
모든 것이 오픈소스로 되어있음
사용하기도 편하고 실제로 large scale 에 특화되 있어서 scaleup 할 때 상당히 용이하게 활용할 수 있음
기존 배포는 C++ 로 되어있는데 wrapping 이 python 으로 되어있어서 python 만 쓰는 분들도 쉽게 활용할 수 있음
FAISS : Library for efficient similarity search
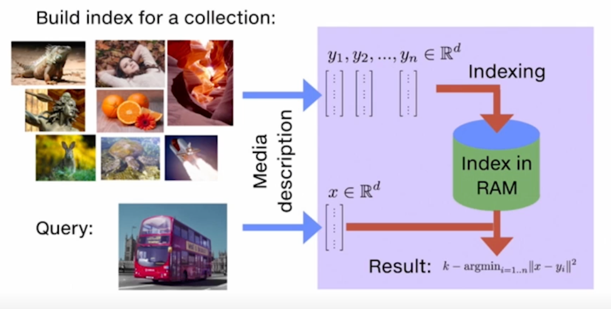
FAISS 는 실제로 indexing 쪽을 도운다고 볼 수 있음
encoding 쪽은 도움을 주고 있는 부분이 아님
Passage Retrieval with FAISS
1) Train index and map vectors
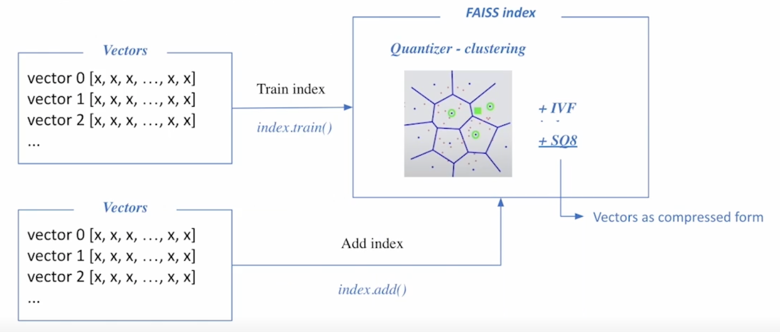
어떤 vector 들을 확보하게 되면 학습을 함
학습을 왜하냐면?
FAISS 를 활용하려면 pruning 즉 cluster 들을 확보해야하는데 당연히 random 하게 cluster 를 지정하게 되면 상당히 비효율적임
그래서 실제로 cluster 들은 data point 들의 분포를 보고 적절한 cluster 를 지정해야 함
cluster 를 지정하기 위해서 학습데이터가 필요하고 또한 그 뿐만 아니라 Scalar Quantization 하는 과정에서도 즉 float32 를 int8 로 바꿔주는 과정에서도 사실상 Quantize 과정이 아주 range 가 큰 float number 를 integer 0~255 사이로 압축시킨 걸 볼 수 있는데 그렇게되면 float number 의 max 가 얼마인지 그리고 minimum 이 얼마인지 그래서 얼마로 scale 하고 얼만큼을 upset 할 것인지에 대해서 파악할 수 있기 때문에 FAISS 로 index 를 building 할 때 학습단계가 필요함
학습단계에서는 이런 cluster 들과 Scalar Quantization 하는 비율과 upset 을 계산하게 됨
이 학습데이터를 통해서 cluster 랑 SQ8 이 정의가 되면 그 다음으로는 실제로 cluster 와 cluster 내에 vector 들을 SQ8 형태로 투입하게 됨
그래서 train 단계가 있는 것이고 그래서 adding 하는 단계가 있음
다만 많은 경우에는 학습할 데이터와 더하는 데이터를 따로하지 않고 다르게하는 경우는 더할 데이터가 너무 많아서 이 전부를 학습하기에는 비효율적일 때 add 할 데이터의 일부를 sampling 해서 학습데이터로 활용함
정말 데이터가 커지는 경우는 대충 40분의 1 정도의 크기나 샘플링해서 쓰는 경우도 있음
2) Search based on FAISS index
* nrpobe : 몇 개의 가장 가까운 cluster 를 방문하여 search 할 것인지
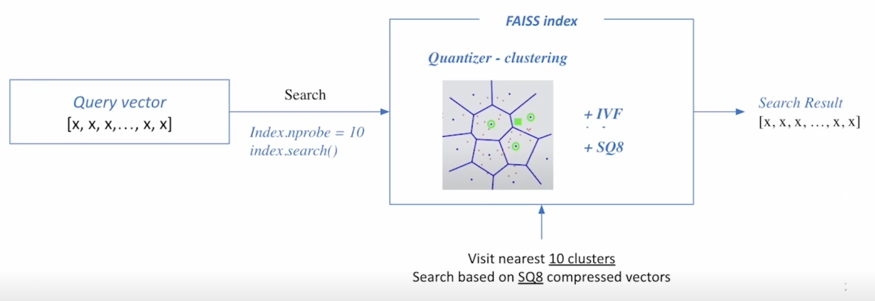
FAISS index 가 만들어지면 inference time 때는 query 가 들어오게 되고 검색을 한 다음에 가장 가까운 cluster 들에 실제로 방문해서 cluster 내에 있는 vector 들을 일일히 비교함으로써 top-k 가장 가까운 문서 벡터들을 뽑아주게되고 물론 여기서 문서벡터라고 하는 건 이해를 돕기위해서 하는 것이고 FAISS 라는 라이브러리는 일반적인 라이브러이기 때문에 어떤 종류의 벡터든지 그 유사성을 계산할 수 있음
예를들면 가장 가까운 10개의 cluster 를 visit 한 다음에 SQ8 베이스로 search 를 하고 top-k 개를 search result 로 내보내게 됨
4. Scaling up with FAISS
FAISS Basics
- brute-force 로 모든 벡터와 쿼리를 비교하는 가장 단순한 인덱스 만들기
준비하기
d = 64 # 벡터의 차원
nb = 100000 # 데이터베이스 크기
nq = 10000 # 쿼리 개수
xb = np.random.random((nb, d)).astype('float32') # 데이터베이스 예시
xq = np.random.random((nq, d)).astype('float32') # 쿼리 예시
인덱스 만들기
index = faiss.IndexFlatL2(d) # 인덱스 빌드하기
index.add(xb) # 인덱스에 백터 추가하기
검색하기
k = 4 # 가장 가까운 벡터 4개를 찾고 싶음
D, I = index.search(xq, k) # 검색하기
# D: 쿼리와의 거리
# I: 검색된 벡터의 인덱스
brute-force 로 모든 vector 와 query 를 비교하는 가장 단순한 index 를 만들어보자
numpy 를 이용해서 matrix 를 만들 수 있고 index 만드는 과정은 생각보다 간단함
faiss.IndexFlatL2() 라는 함수를 이용해서 dimension 을 정의해주고 더해주면 됨
왜 여기는 학습을 하지않냐고 물어볼 수 있는데 학습이 필요없는 이유는 아까 봤던 Quantization, pruning 과 scalar Quantization 을 여기서 활용하지 않기 때문에 학습이 필요가 없는 것임
2가지의 Quantization 을 활용할 때만 학습이 필요함을 유의하자!
그래서 index.train 은 없고 index.add 만 있음
그 다음은 검색으로 넘어가는데 top-k 로 몇개를 retrieval 할지 k 를 정해주고 index.search() 를 해서 해당하는 쿼리를 넣어주고 k 도 같이 넣어줘서 D, I 가 나오게되고 D 는 쿼리와의 실제 거리 즉 점수이고 I 는 각각의 passage 의 index id 가 됨
IVF with FAISS
- IVF 인덱스 만들기
- 클러스터링을 통해서 가까운 클러스터 내 벡터들만 비교함
- 빠른 검색 가능
- 클러스터 내에서는 여전히 전체 벡터와 거리 비교 (Flat)
IVF 인덱스
nlist = 100 # 클러스터 개수
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFFlat(quantizer, d, nlist) # Inverted File 만들기
index.train(xb) # 클러스터 학습하기
index.add(xb) # 클러스터에 벡터 추가하기
D, I = index.search(xq, k) # 검색하기
FlatL2 를 활용해서 brute-force search 알고리즘을 만들어봤는데 바로 직전에 말했던 Quantization 을 통해서 approximation 을 해야함
approximation 을 위한 Quantization 은 간단함
pruning 을 알아보자
pruning 은 IVF 라는 이름으로 faiss 에서 찾을 수 있는데 먼저 quantizer 를 만들어야 함
quantizer 같은 경우는 클러스터에서 거리를 계산할 때 어떻게 계산할 것인가에 대한 것이고 클러스터끼리 거리를 계산하는 방법론은 L2 방식(거리를 계산)을 취할 것이기 때문에 exhaustive 하게 거리를 계산하기때문에 IndexFlatL2 를 활용해서 quantizer 를 만들어주게 됨
클러스터와 쿼리의 거리를 계산하는 방법론을 정의했으면 quantizer 를 활용해서 faiss.IndexIVFFlat() 클래스로 초기화해줌
quantizer 를 활용해서 클러스터를 만들겠다는 의미임
여기서 중요한 parameter 가 nlist 인데 클러스터의 개수를 몇개로 할 것인가를 정의해줌
그다음에 train 을 하게되면 train 과정중에서 IndexIVFFlat 이 학습데이터 xb 를 활용해서 nlist 개수만큼 클러스터를 k-means 알고리즘으로 생성함 - 시간이 좀 걸림
그 다음에 다시 index.add(xb) 를 하게 됨
위에서 말한것처럼 xb 가 꼭 다를 필요는 없고 보통 같음 다만 xb 가 너무 큰 경우 학습할 때 너무 오래걸릴 수 있으므로 xb 를 일부 sampling 해서 학습을 한 다음에 retrieval 하는 대상을 뺄 수 없으므로 더해주는건 다 더해줌 그다음에 쿼리가 들어왔을 때 search 를 하는 방식을 똑같이 취함
이렇게되면 가장 가까운 몇개의 클러스터만 방문해서 답을 내옴
IVF-PQ with FAISS
- 벡터 압축 기법 (PQ) 활용하기
- 전체 벡터를 저장하지 않고 압축된 벡터만을 저장
- 메모리 사용량을 줄일 수 있음
IVF-PQ 인덱스
nlist = 100 # 클러스터 개수
m = 8 # subquantizer 개수
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFPQ(quantizer, d, nlist, m, 8) # 각각의 sub-vector 가 8 bits 로 인코딩 됨
index.train(xb)
index.add(xb)
D, I = index.search(xq, k) # 검색하기
SQ 말고 PQ 라는 압축기법이 있는데 SQ 보다 좀 더 압축량을 높일 수 있고 자세하게는 faiss 웹페이지에서 보는 것을 추천하고 여기선 다루지 않겠음
SQ 와 마찬가지로 학습이 필요하고 학습을 하는 방법론이 상당히 비슷하지만 훨씬 더 줄일 수 있음
SQ 같은 경우는 4-byte 를 1-byte 로 줄이는 정도였다면 PQ 는 경우에따라서 768 개의 dimension vector 의 size 가 768 x 4 라고 한다면 그걸 예를 들면 100-byte 정도로 줄일 수 있음
예를들면 배수로 치면 4배가 아니라 20배 정도로 줄일 수 있음
이런 것들은 challenge 에서 필요하다고 하면 활용하면 좋을 듯
그렇다고 하더라도 기본적으로 먼저 SQ 를 먼저해보시고 나중에 PQ 가 필요하다고 생각이 들면 넘어가는 것을 추천
Using GPU with FAISS
- GPU 의 빠른 연산 속도를 활용할 수 있음
- 거리 계산을 위한 행렬곱 등에서 유리
- 다만, GPU 메모리 제한이나 메모리 random access 시간이 느린 것 등이 단점
단일 GPU 인덱스
res = faiss.StandardGpuResources() # 단일 GPU 사용하기
index_flat = faiss.IndexFlatL2(d) # 인덱스 (CPU) 빌드하기
# GPU 인덱스로 옮기기
gpu_index_flat = faiss.index_cpu_to_gpu(res, 0, index_flat)
gpu_index_flat.add(xb)
D, I = gpu_index_flat.search(xq, k) # 검색하기
GPU 에서 활용할 수 있는 것은 IndexFlatL2 만 활용할 수 있음
다른 클래스나 search 알고리즘은 활용하기 어려운 경우가 많음
Using Multiple GPUs with FAISS
- 여러 GPU 를 활용하여 연산 속도를 한층 더 높일 수 있음
다중 GPU 인덱스
cpu_index = faiss.IndexFlatL2(d)
# GPU 인덱스로 옮기기
gpu_index = faiss.index_cpu_to_all_gpus(cpu_index)
gpu_index.add(xb)
D, I = gpu_index.search(xq, k) # 검색하기
먼저 single GPU 를 활용해보고 더 빠르게 하는게 필요하다고 생각이들면 multi GPU 를 생각해보시되 대부분의 경우는 multi GPU 까지 가는 경우는 없을 것이라 예상함

댓글남기기