Day_47 01. Passage Retrieval - Sparse Embedding

Passage Retrieval - Sparse Embedding

1. Introduction to Passage Retrieval

Passage Retrieval

질문(query)에 맞는 문서(passage)를 찾는 것

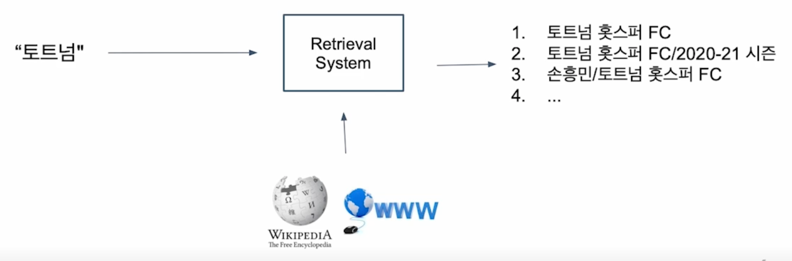
목표로 하는 것은 “토트넘” 이라는 질문이 들어왔을 때 Passage Retrieval 한 문제는 이 웹상에 혹은 위키피디아 상에 관련된 문서를 가져오는 시스템을 의미함

왜 이런 시스템을 만드는것에 관심이 있을까?

Passage Retrieval 과 MRC 를 연결하면 Open-domain Question Answering 을 할 수 있음

Passage Retrieval with MRC

Open-domain Question Answering: 대규모의 문서 중에서 질문에 대한 답을 찾기

• Passage Retrieval 과 MRC 를 이어서 2-Stage 로 만들 수 있음

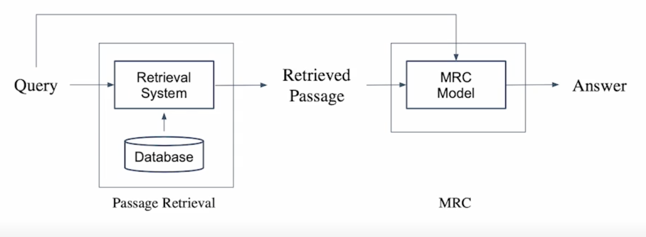
Passage Retrieval 모델은 질문에 관련된 지문을 찾아서 MRC 모델에 넘겨주게되고 MRC 모델은 그 지문을 보고 질문을 다시 읽어봄으로써 아주 정확한 답변을 낼 수 있는 2-Stage 의 pipeline 이라고 보면 됨

Overview of Passage Retrieval

Query 와 Passage 를 임베딩한 뒤 유사도로 랭킹을 매기고, 유사도ㅇ가 가장 높은 Passage 를 선택함

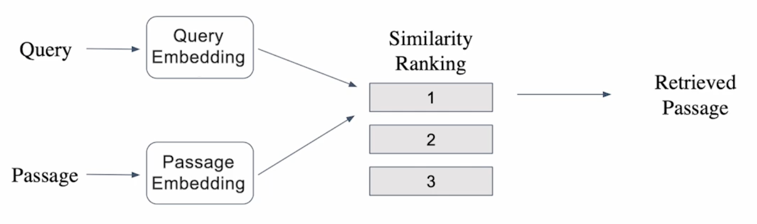
지문에 대한 embedding 은 미리 해둠으로써 효율성을 도모하고 그 다음에 들어온 지문에 대해서 각 passage 에 임베딩과 similarity score 를 재게됨 일반적으로 많이 쓰이는 score 는 고차원 space 에서 서로의 거리가 얼마나 되는지를 보거나 inner product 같은 서로의 dot product 를 계산해서 높은 score 를 내는 passage 를 찾는 방식을 취하게 됨

이 similarity score 가 무엇이 되었든 similarity score 를 모든 passage 에 관해서 잰다음에 이 score 들을 ranking 을 매겨서 가장 높은 문서 순서대로 내보내주는 방식을 취하게 됨

2. Passage Embedding and Sparse Embedding

Passage Embedding Space

• Passage Embedding 의 벡터 공간
• 벡터화된 Passage 를 이용하여 Passage 간 유사도 등을 알고리즘으로 계산할 수 있음

결국은 Passage 를 vector space 에 맵핑하려는 것이고 이 vector space 라 함은 고차원 여러개의 숫자로 이루어져있는 point 들이 모여있는 고차원적인 추상적인 공간이라고 보면 될 것 같음

이걸 3차원 space 에서 visualize 한다면 그림에서 보다시피 일종의 3차원 상의 점이될텐데 결국엔 2개의 문서의 유사도 또는 어떤 문서와 질문의 유사도를 저 vector space 상에서 거리로 계산을 한다고 보면 됨

Sparse Embedding 소개

sparse 라는 의미는 dense 의 반대어로서 0이 아닌 숫자가 상당히 적게있음을 의미 함

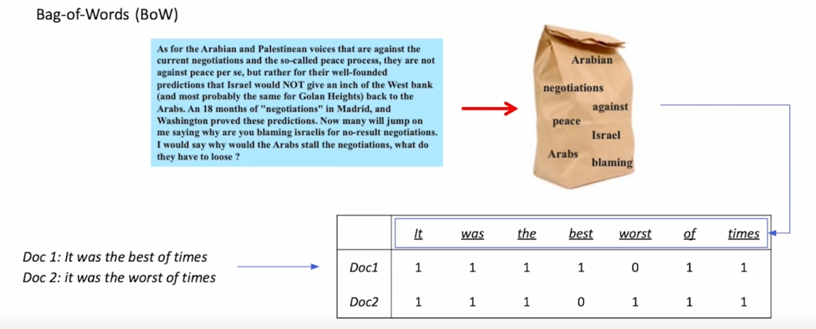
가장 대표적인게 Bag-of-Words 라는 방법론임

문서가 주어졌을 때 문서를 embedding space 로 맵핑하기 위해서 각 문서의 존재하는 단어들을 1이나 0으로 존재하면 1 없으면 0으로 표현하여 아주 긴 vector 로 표현하는 것을 의미함

이런 경우에는 특정 단어가 존재하는지 안하는지로 표현하다보니 vector 의 길이는 전체 우리가 고려하고 있는 vocabulary 의 size 와 동일하게 됨

예를들면 우리 vocabulary 에 30만개의 단어가 있다고 한다면 모든 문서가 30만 vector space 로 맵핑을 하게됨

그리고 각각의 dimension 은 하나의 단어에 해당하게 되는데 그림 아래쪽에서 “It”, “was”, “the”, “best”, “worst”, “of”, “times” 가 vocabulary 라고 한다면 각 단어가 해당 문서 doc1 과 doc2 에 있는지 없는지에 따라서 1과 0이 표시된 걸 볼 수 있음

물론 이 경우는 vocabulary 가 상당히 적은 편이고 문서 또한 단어가 상당히 적은편이라 할 수 있습니다만 실제로는 vocabulary size 가 몇 십만 혹은 몇 백만이 될 수도 있고 문서의 길이도 마찬가지로 6~7개 단어가 아니라 수백개 혹은 수천개 단어로 이루어질 수 있음

1. BoW 를 구성하는 방법 $\rightarrow$ n-gram
   • unigram (1-gram) : It was the best of times => It, was, the, best, of, times
   • bigram (2-gram) : It was the best of times => It was, was the, the best, best of, of times
2. Term value 를 결정하는 방법
   • Term 이 document 에 등장하는지 (binary)
   • Term 이 몇번 등장하는지 (term frequency), 등. (e.g. TF-IDF)

n-gram 에서 n 이 늘어나면 늘어날수록 기하급수적으로 vocabulary size 가 늘어나기 때문에 n 을 키우는게 항상 desirable 한 것은 아니고 다만 bigram 까지는 보통 활용하는 편이고 경우에 따라서는 trigram 도 활용하는 경우가 있음

가장 vanila 한 BoW 같은 경우는 Term 이 문서 내에 등장하는지 안하는지만 보도록 되어있고 즉 binary 0 이나 1로 표현이 되는건데 이런 방법은 사실 굉장히 vanila 한 방법이고 더 잘할수 있음

조금 더 잘할수 있는 방법이 TF-IDF 라는 더 advanced 한 방법이 있음

Sparse Embedding 특징

1. Dimension of embedding vector = number of terms
   • 등장하는 단어가 많아질수록 증가
   • N-gram 의 n 이 커질수록 증가

1. Term overlap 을 정확하게 잡아 내야 할 때 유용
2. 반면, 의미(semantic)가 비슷하지만 다른 단어인 경우 비교가 불가

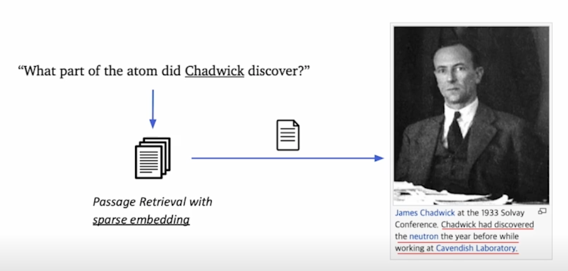
3. TF-IDF

TF-IDF (Term Frequency - Inverse Document Frequency) 소개

• Term Frequency (TF) : 단어의 등장 빈도
• Inverse Document Frequency (IDF) : 단어가 제공하는 정보의 양

ex) It was the best of times
$\rightarrow$ It, was, the, of : 자주 등장하지만 제공하는 정보량이 적음 $\rightarrow$ best, times : 좀 더 많은 정보를 제공

특정 단어의 등장빈도를 보는 방식으로 진행하게 됨

그리고 단어의 등장빈도만 고려하는 것이 아니라 단어가 제공하는 정보의 양도 반대로 얘기하자면 단어가 얼만큼 덜 등장하는지를 봐서 이 두개의 숫자를 곱해줌으로써 최종 수치를 계산하게 됨

이걸 어떻게 해석해야하냐면?

어떤 문서내에 단어가 많이 등장했는데 그 단어가 전체문서에서는 등장하는 경우가 별로 없더라 이러면 이 단어는 그 문서내에서 상당히 중요한 것임

Term Frequency (TF)

해당 문서 내 단어의 등장 빈도

1. Raw count
2. Adjusted for doc length: raw count / num words (TF)
3. Other variants: binary, log normalization, etc.

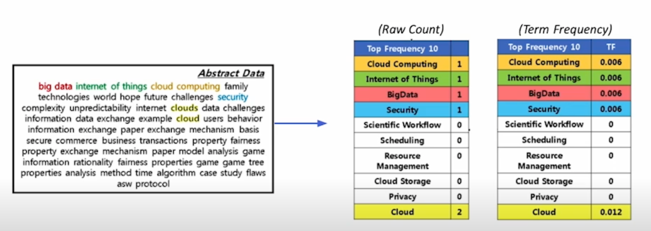
먼저 특정 단어가 해당 문서에서 몇번 나오는지를 세고 이게 결정적으로 BoW 와 다른점임

BoW 는 0 이나 1이었던 반면에 TF 는 특정단어가 2번 등장하면 1이 아니라 2가 됨

여기서 끝나는 것이 아니라 이걸 normalize 해줌

보통은 raw count 그대로 쓰지 않고 실제 문서내에서 총 단어의 개수가 몇개인지를 봄으로써 비중을 비교적 비율로 나타내게 되고 그리고 총합이 1 이하일 수 있도록 하는 것임

Inverse Document Frequency (IDF)

단어가 제공하는 정보의 양

$IDF(t) = log \frac{N}{DF(t)}$

• Document Frequency (DF) = Term t 가 등장한 document 의 개수
• N : 총 document 의 개수

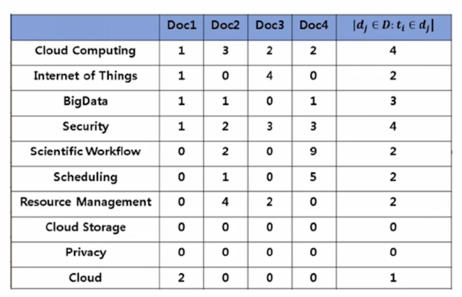
총 document 의 개수 N 을 구하고 그 다음에 특정 term 의 document frequency 를 구하게 됨

즉, 특정 Term 이 등장한 document 의 개수임

어떻게 해석하면 되냐면?

예를 들면 “the”, “is” 같은 아주 자주 등장하는 단어의 경우는 DF 가 상당히 높을 것임

대부분의 문서에 들어가있기 때문에 사실상 문서가 100개라고 한다면 100개 모두 “the” 가 한번쯤은 들어갈 것임

그러면 DF(t) score 는 100이 됨 그리고 N 도 100이 되기 때문에 100/100 은 1이되고 여기에 log 를 씌워주게 되면 0이 됨

즉 “the” 와 같은 단어 모든 문서에 등장하는 단어 같은 경우는 IDF score 가 0점이 됨

그런데 예를 들면 어떤 단어가 한 문서에서만 등장할 수 있음

이런 경우 N 은 똑같이 100인데 DF(t) 가 1이 되기 때문에 N / DF(t) 는 100이 되고 이 숫자를 log 하게 되면 2진법을 썼을때는 암산할 수 없겠지만 10진법을 썼을때는 $log10$ 은 2가되서 꽤 큰 수치가 TF 에 곱해지게 됨

여기서 중요한 점은 TF 와 다르게 IDF 는 각 Term 에 특정되고 문서에는 무관하다는 점임

Combine TF & IDF

TF-IDF(t, d) : TF-IDF for term t in document d,

\[TF(t, d) \times IDF(t)\]

i) ‘a’, ‘the’ 등 관사 $\rightarrow$ Low TF-IDF

TF 는 높을 수 있지만, IDF 가 0에 가까울 것
(거의 모든 document 에 등장 $\rightarrow$ $N \approx DF(t) \rightarrow log(N/DF) \approx 0$)

ii) 자주 등장하지 않는 고유 명사 (ex. 사람 이름, 지명 등) $\rightarrow$ High TF-IDF

IDF 가 커지면서 전체적인 TF-IDF 값이 증가

TF-IDF 계산하기

실험할 데이터 :

문서 제목	문서 내용
음식	주연은 과제를 좋아한다
운동	주연은 농구와 축구를 좋아한다
영화	주연은 어벤져스를 가장 좋아한다
음악	주연은 BTS의 뷔가 가장 잘생겼다고 생각한다

토크나이저

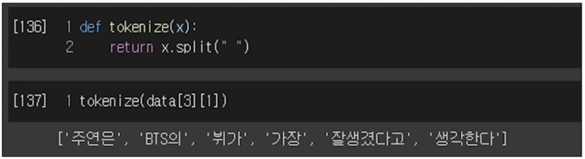
토크나이징을 해야 term 들을 정의할 수 있음

Term Frequency (TF) : 단어의 등장 빈도
TF(t, d) : TF for term t and document d

계산 결과에 0 또는 1 밖에 없는 이유: 예시에선 각 문서마다 특정 단어가 1번 또는 0번 나왔기 때문

Inverse Document Frequency (IDF) : 단어가 제공하는 정보의 양

\[IDF(t) = log \frac{N}{DF(t)}\]

• 자주 출현한 단어들은 IDF 값이 낮은 것을 확인할 수 있음
• IDF 값은 문서에 상관없이 항상 일정한 값을 가짐을 확인할 수 있음

TF-IDF 계산

\[TF(t, d) \times IDF(t)\]

위에서 계산한 두개의 table 을 그대로 곱해주면 됨

• 각 문서가 가지고 있는 고유한 단어가 높은 TF-IDF 값을 가진 것을 확인할 수 있음
• 자주 출현한 단어들은 TF-IDF 값이 낮은 것을 확인할 수 있음

TF-IDF 를 이용해 유사도 구해보기

목표 : 계산한 문서 TF-IDF 를 가지고 질의 TF-IDF 를 계산한 후 가장 관련있는 문서를 찾기

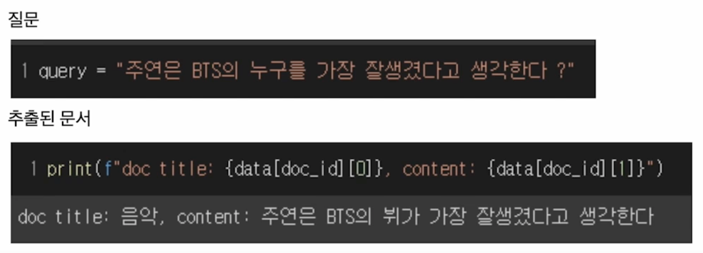
\[질문 : 주연은 BTS 의 누구를 가장 잘생겼다고 생각한다?\]

문서의 TF-IDF 를 구해놨으면 마지막으론 질문쪽에서 똑같은 방식으로 질문을 문서라 생각하고 TF-IDF score 를 구한다음에 두개의 vector 의 유사도를 구해주면 됨

유사도를 구하는 방식은 여러가지가 있는데 보통 TF-IDF 같은 경우는 cosine distance 를 구하게되고 사실상 normalize 를 한 다음엔 두개를 inner product 를 하게되면 cosine distance 가 됨

목표: 계산한 TF-IDF 를 가지고 사용자가 물어본 질의에 대해 가장 관련있는 문서를 찾자

1. 사용자가 입력한 질의를 토큰화
2. 기존에 단어 사전에 없는 토큰들은 제외
3. 질의를 하나의 문서로 생각하고, 이에 대한 TF-IDF 계산
4. 질의 TF-IDF 값과 각 문서별 TF-IDF 값을 곱하여 유사도 점수 계산

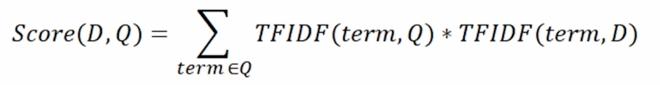
1. 가장 높은 점수를 가지는 문서 선택

목표: 계산한 TF-IDF 를 가지고 사용자가 물어본 질의에 대해 가장 유사한 문서를 검색하기

BM25 란?

TF-IDF 의 개념을 바탕으로, 문서의 길이까지 고려하여 점수를 매김

• TF 값에 한계를 지정해두어 일정한 범위를 유지하도록 함
• 평균적인 문서의 길이 보다 더 작은 문서에서 단어가 매칭된 경우 그 문서에 대해 가중치를 부여
• 실제 검색엔진, 추천 시스템 등에서 아직까지도 많이 사용되는 알고리즘

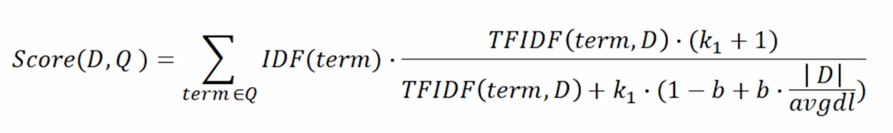
이 공식을 그대로쓰거나 좀 더 튜닝해서 쓰는 방법 추천

Further Reading

• Pyserini BM25 MSmarco documnet retrieval 코드
• Sklearn feature extractor ⇒ text feature extractor 부분 참고

---

실습

from datasets import load_dataset
dataset = load_dataset('squad_kor_v1')

문서들만 따로 빼서 가져와보도록 하자

corpus = list(set([example['context'] for example in dataset['train']]))

set 을 사용한 이유는 korquad dataset 에 중복된 context 가 있기 때문에 그래서 set 을 해줬다가 list 로 변경해줌

len(corpus)

약 9600개임을 알 수 있음

corpus[0]

하나를 가져오면 문서 지문을 볼 수 있음

그 다음엔 tokenize 를 하겠음

가장 기본적인 tokenization 은 space 임

tokenizer_func = lambda x: x.split(' ')

space 로 tokenization 하는 function 을 정의해줌

tokenizer_func(corpus[0])[:10]

이렇게 됨을 알 수 있음

TF-IDF 를 계산하기 위해서는 실제로 직접하지 않고 scikit-learn 에 있는 TfidfVectorizer 를 활용할 거임

from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(tokenizer=tokenizer_func, ngram_range=(1, 2))

vectorizer.fit(corpus)

fit 하게되면 학습한다고 생각하면 되는데 neural net 을 학습하는 것과는 차이가 있음

sp_matrix = vectorizer.transform(corpus)
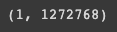
sp_matrix.shape

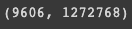
9606 이 text 지문의 개수이고 1272768 은 unigram, bigram 을 포함해서 지문 내에 등장하는 term 들의 개수임

다음으로는 table 을 잘 활용하기 위해 pandas 를 사용하겠음

df = pd.DataFrame(sp_matrix[0].T.todense(), index=vectorizer.get_feature_names(), colnames=['TF-IDF'])
df = df.sort_values('TF-IDF', ascending=False)
print(df.head(10))

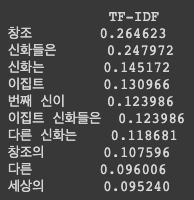
간단히 visualize 하기 위한 용도이고 sp_matrix[0] 은 sparse matrix 의 첫번째 문서에 해당하는 vector 만 가져와서 table 화 해서 보게되면 위 처럼 나옴을 볼 수 있음

각 단어에 해당하는 TF-IDF 값들을 볼 수 있음

sparse matrix 의 일부임

이렇게 vector 를 만들었으니 retrieval 해볼텐데 학습데이터셋에서 하나의 질문을 랜덤하게 고른자

import random
import numpy as np

random.seed(1)
sample_idx = random.choice(range(len(dataset['train'])))

query = dataset['train'][sample_idx]['question']
ground_truth = dataset['train'][sample_idx]['context']

이렇게 정의해주고

query vector 를 vectorizer 를 활용해서 변경하면 됨

query_vec = vectorizer.transform([query])
query_vec.shape

shape 의 행이 1로 되어있는데 편의상 matrix 로 표현하기 위해서 1이 붙어있는거고 실제로는 1-dimensional vector 임

마지막으론 결과를 계산하게 됨

result = query_vec * sp_matrix.T
result.shape

각각의 지문과 현재 질문에 유사도를 9606개의 숫자로 나타낸 것임

그 다음엔 여기서 가장 높은 숫자가 나오는 걸 찾으면 됨

sorted_result = np.argsort(-result.data)
doc_scores = result.data[sorted_result]
doc_ids = result.indices[sorted_result]

top 3 를 봐보자

k = 3
doc_scores[:k], doc_ids[:k]

첫번째 3개의 문서는 id 가 6167번, 1950번, 4329번 임을 알 수 있고 각각 score 가 0.189, 0.036, 0.033 임을 알 수 있음

그 다음에 실제 해당 query 에 해당하는 문서가 어떤 문서인지 내용까지 같이 보여주는 print 를 한번 해보자

결과에 대한 해석이다

print("[Search query]\n", query, "\n")

print("[Ground truth passage]")
print(ground_truth, "\n")

for i in range(k):
    print("Top-%d passage with score %.4f" % (i + 1, doc_scores[i]))
    doc_id = doc_idx[i]
    print(corpus[doc_id], "\n")

정답과 top-1 이 일치함을 볼 수 있고 이처럼 TF-IDF 가 잘 작동했다는 것을 알 수 있음